9. Методика наблюдений и метод учета урожая

Учет урожая проводился сопряжено с закладкой почвенных разрезов, согласно методике полевого опыта с делянок площадью 1 м². Для этого в производственных посевах зерновых культур в четырехкратной повторности отобраны снопы, которые доставлялись в лабораторию и в лаборатории проводился разбор снопа.

Такой спряженный учет урожая позволяет определить зависимость эффективного плодородия от потенциального, т.е. как зависит определяемая урожайность от изученных свойств почв.

10. Статистические методы обработки полученных результатов

Для статистической обработки таких параметров почв, как мощность гумусового горизонта, содержание гумуса, подвижных форм азота, фосфора и обменного калия, поглощенных оснований, содержания физической глины и ила, а так же выявления тенденций их изменения были использованы следующие алгоритмы:

1. Средняя арифметическая – х = X/n ,

где n – число значений Х

2. Дисперсия S² = (Х – 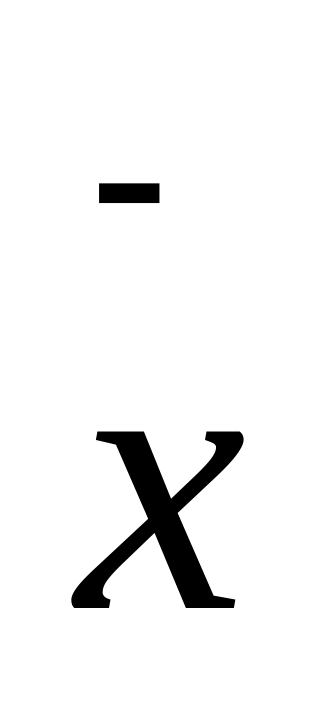)²/n-1

3. Стандартное отклонение – S = ;

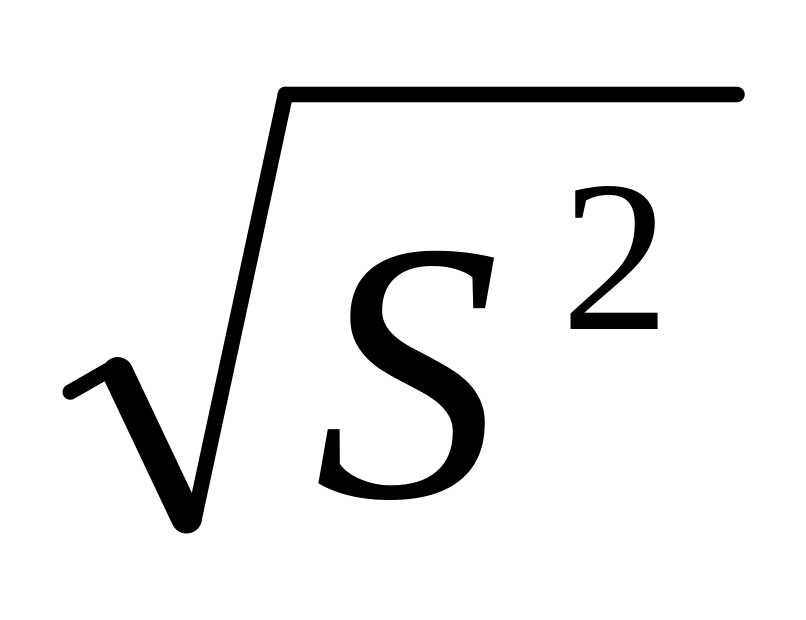4. Коэффициент вариации – V = S100/X;

5. Ошибка средней - S_x = S/ 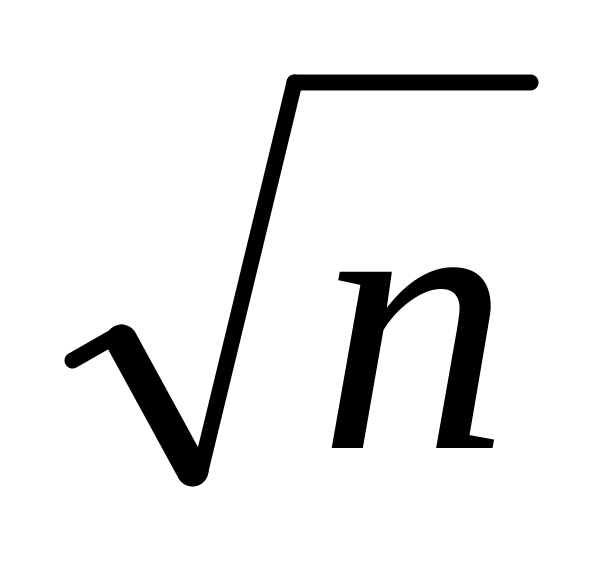; (Доспехов, 1979).

Для установления связей между большим разнообразием показателей (экспозицией, крутизной, длинной склонов, видовым разнообразием почв, морфологическими, физическими, физико-химическими свойствами почв и урожайностью зерновых культур) использован информационно-логический анализ в модификации Ю.Т. Пузаченко, Л.О. Корпачевского, Н.А. Взнуздаева (1970). Помимо этих авторов этот анализ использовался в работах Л.М. Бурлаковой (1973). В основу данного анализа положены представления об измеримости информации, передаваемой изучаемому явлению, как от одного параметра, так и от их совокупности.

Если обозначить изучаемое явление через А, то каждое его значение можно выразить через а₁, а₂, …, а_k или в общей форме через а_i. Таким образом, если А обозначает весь набор возможных параметров, то а_i обозначает отдельный ранг параметра. Не зная закономерностей изменения А, мы можем принять, что появление а_i – есть случайное событие, тогда частота появления каждого ранга А= а_i – есть оценка условной вероятности р(а₁), р(а₂)., р(а_k). Вероятность а_i находится по формуле р(а_i)=Na_i/N, где Na_i – число случаев появления а_i, N – общее число наблюдений. Наше суждение о появлении того или иного параметра явления в какой-то мере неопределенно. Величину этой неопределенности можно оценить количественно. Она обозначается как Н(А) = ∑р(а_i)Log₂р(а_i), т.е. неопределенность появления разных значений А равна сумме произведений вероятности появления каждого ранга р(а_i) на двоичный логарифм этой же вероятности. Если изучается зависимость явления А от фактора В мы составляем свое распределение явления А. В этом случае вероятность рангов а₁, а₂ ., а_к в каждом ранге В обозначается через р(а_i/b_j). Для каждого в_j можно рассчитать неопределенность Н(А/в_j), которая равна ∑р(а_i/b_j)Log₂р(а_i/b_j). Если между А и В есть зависимость, то Н(А) = Н(А/b_j). Разность этих величин служит мерой того, насколько наше суждение об А при b_j становится более определенным, чем при значении только распределения А. Эта мера обозначается как I(А/b_j) и называется информацией об А, содержащейся в b_j. Количество информации поступающей от В к А оценивается как ∑р(b_j)I(А/b_j), т.е. сумма произведения вероятности ранга b_j Т(А,В). Значение Т(А,В) зависит не только от связи между А и В, но и от величины их неопределенностей. Чем больше неопределенность В, тем больше информации передается к явлению А. Для устранения влияния величины неопределенности вводится коэффициент эффективности передачи информации от фактора В к явлению А – К(А,В), который равен К(А,В)=Т(АВ)/Н(В). Наибольшее значение имеет фактор с наибольшим коэффициентом К. Таким образом, при помощи К можно установить степень влияния каждого параметра на изучаемое явление и расположить их по мере убывания коэффициента эффективности канала связи (К).