Проверка адекватности модели

Проверка адекватности модели заключается в определении ее значимости и наличии или отсутствии систематической ошибки.

Проверка значимости модели

Сначала проверяется значимость параметров уравнения. Если, например, параметр является незначимым, то необходимо с помощью метода наименьших квадратов получить соответствующее уравнение из которого определяется значение параметра .

Проверка значимости осуществляется на основе t – критерия Стьюдента, т.е. проверяется гипотеза о том, что параметр, измеряющий связь, равен нулю.

Средняя ошибка параметра равна:

=0,75 (82)

а для параметра :

=0,00092 (83) Расчетные значения t- критерия вычисляются по формуле:

; , (84)

Параметр считается значимым, если (37,31>2,01; 9,75>2,01)

Параметр лежит в пределах , -7,8982 (-9,40;-6,39),

а параметр - , 0,0352 (0,033; 0,037).

Значимость уравнения регрессии в целом определяется с помощью F – критерия Фишера:

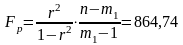(85)

где - число параметров в уравнении регрессии.

Расчетное значение F сопоставляется с табличным для числа степеней свободы при заданном уровне значимости (например, ).

Если (864,74>4,052) уравнение считается значимым.

Проверка наличия или отсутствия систематической ошибки

1. Проверка свойства нулевого среднего.

Рассчитывается среднее значение ряда остатков

. (86)

Если оно близко к нулю, то считается, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего, иначе – модель неадекватна по данному критерию.

2. Проверка случайности ряда остатков.

Осуществляется по методу серий. Серией называется последовательность расположенных подряд значений ряда остатков, для которых разность имеет один и тот же знак, где - медиана ряда остатков.

Если модель хорошо отражает исследуемую зависимость, то она часто пересекает линию графика исходных данных и тогда серий много, а их длина невелика. Иначе – серий мало и некоторые из них включают большое число членов.

Иногда медиана ряда остатков априорно принимается равной нулю, исходя из предположения симметричности распределения ошибок около нулевого среднего, тогда в качестве серий рассматриваются расположенные подряд ошибки с одинаковыми знаками. Далее подсчитывается число серий и длина максимальной из них . Полученные значения сравниваются с критическими

(87)

(88)

(квадратные скобки означают округление вниз до ближайшего целого).

Если выполняется система неравенств:

, , (89)

то модель признается адекватной по критерию случайности, если хотя бы одно из неравенств нарушено, то модель признается неадекватной по данному критерию.

3. Проверка независимости последовательных остатков.

Является важнейшим критерием адекватности модели и осуществляется с помощью коэффициента Дарбина-Уотсона:

(90)

Последовательные остатки независимы, т.к. близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.

Для проверки существенности положительной автокорреляции остатков значение сравнивается с и : (2 > 1,64 > 1,5) - гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию.

4. Проверка постоянства дисперсии остатков.

Если на графике остатков они укладываются в симметричную относительно нулевой линии полосу шириной (модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.

Кроме визуальной оценки постоянства дисперсии существуют и более точные методы, например, тест Гольдфельда-Квандта. Суть теста заключается в следующем. Все n наблюдений упорядочиваются по возрастанию значений переменной x и производится оценка параметров регрессий для первых n₀ и последних n₀ наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение n₀ порядка n/3. Вычисляется расчётное значение статистики Фишера

_где - суммы квадратов остатков для первых n₀ и последних n₀ наблюдений соответственно.

_Если F_р < F_кр (0,85<2,48), то делается вывод о постоянстве дисперсии.

По совокупности четырех критериев делается вывод о принципиальной возможности использования модели: если модель адекватна по критериям постоянства дисперсий и нулевого среднего и хотя бы по одному из двух других критериев, то она может быть принята для использования, хотя и не признается полностью адекватной.