Истечение паров, жидкостей и газов.

Процесс истечения – процесс переноса вещества из области с одним давлением в область с другим.

Действительный процесс истечения характеризуется необратимыми потерями и неравномерностью распределения скоростей в потоке. В теории истечение рассматривается, как обратимый процесс, а переход к реальным характеристикам осуществляется с помощью двух коэффициентов: коэффициента скорости - и коэффициента расхода - , причём эти коэффициенты определяются экспериментальным путём. Оба коэффициента показывают различия между теоретическими и действительными величинами.

Нас интересуют следующие величины:

1. Линейная скорость - , .

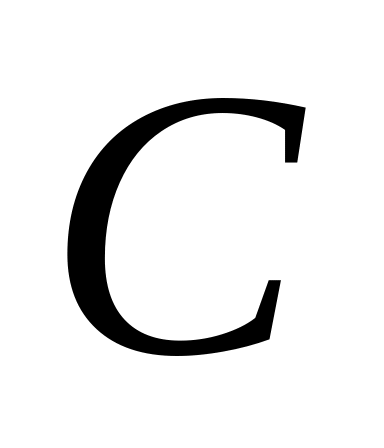2. Массовая скорость - , .

3. Массовый расход - , .

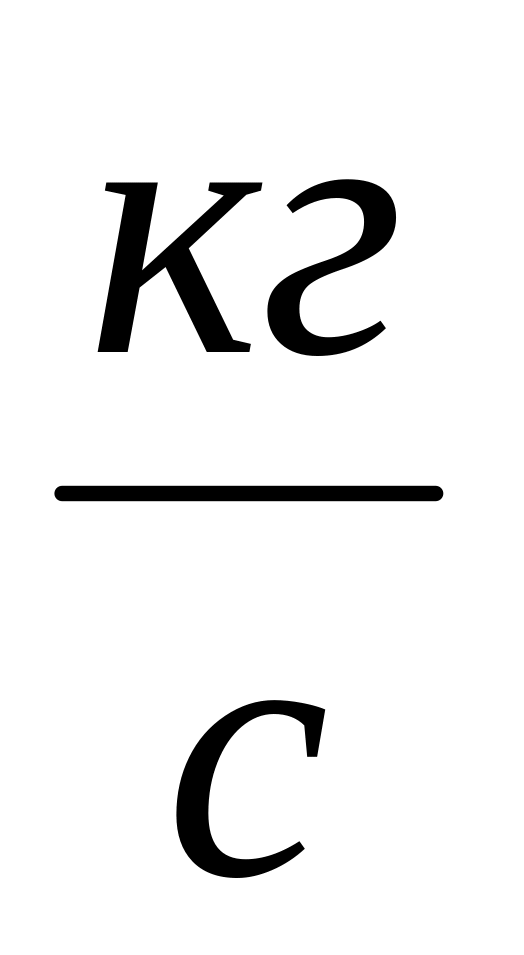Задача решается на базе следующих уравнений:

1. Первое начало термодинамики: .

2. Уравнение процесса:

   1. Политропный процесс: .

   2. Адиабатный процесс: .

3. Уравнение неразрывности в интегральном виде: .

4. Уравнение состояние.

Основные соотношения процесса истечения.

Уравнение распределения потенциальной работы:

.

Так как рассматриваются обратимые потери, то .

Так как рассматривается чистое движение, то .

Следовательно: .

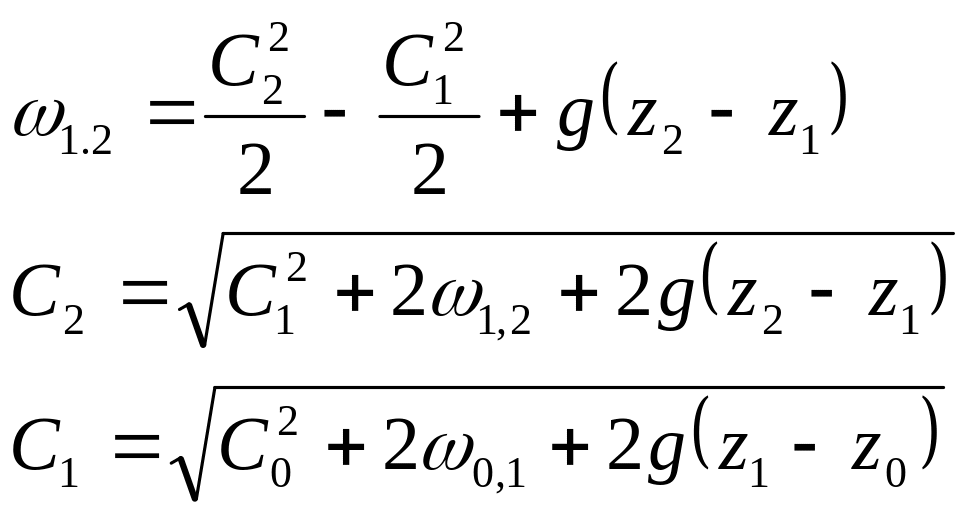
Так как рассматриваются короткие каналы, то , .

Выражение для линейной скорости: .

Выражение для массовой скорости: .

Выражение для массового расхода: .

Основные исходные соотношения.

Уравнение для линейной скорости: .

Уравнение для массовой скорости: .

Уравнение для массового расхода: .

Истечение несжимаемой (капельной) жидкости.

Условия не сжимаемости жидкости: , .

Рассматриваем изохорный процесс. Потенциальную работу можно найти по следующей формуле: .

Подставив это в уравнение для линейной скорости, получим: .

Графическое представление зависимости скорости то перепада давления:

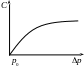
Подставив это в уравнение для массовой скорости, получим: .

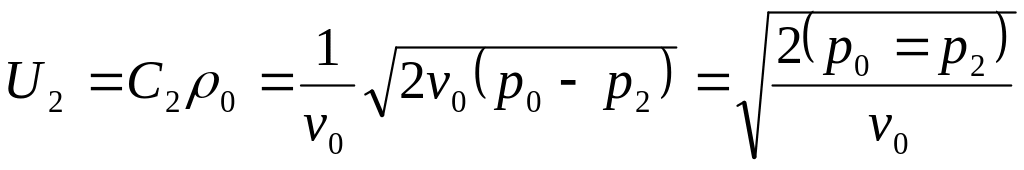Подставив это в уравнение для массового расхода, получим: .

Действительная линейная скорость отличается от теоретической, поэтому вводят коэффициент скорости , где - действительная линейная скорость, - теоретическая линейная скорость. Поэтому действительную линейную скорость можно найти по формуле: .

При течении жидкости в трубе с переменным сечением наблюдается отрыв струи от стенок и площадь сечения течения становится меньше площади сечения трубопровода. В связи с этим вводят коэффициент сжатия струи , при этом он лежит в пределах от 0.6 до 1. Если профиль канала параболический, то .

Действительный массовый расход можно найти по формуле: , где - коэффициент расхода.

Вопрос № 24.

Истечение сжимаемых жидкостей (паров и газов).

Условия сжимаемости жидкости: , .

Рассматриваем политропный процесс истечения: . В случае, если , то получаем адиабатный процесс истечения.

Потенциальную работу можно найти по следующей формуле: , где 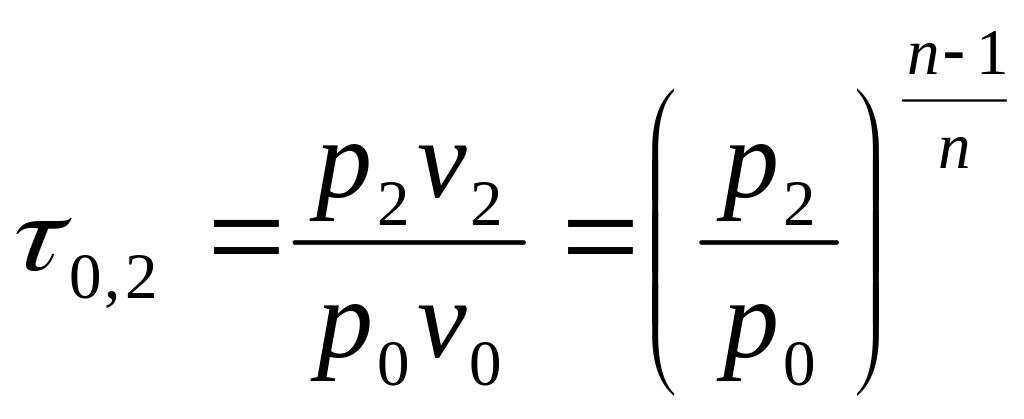. Тогда 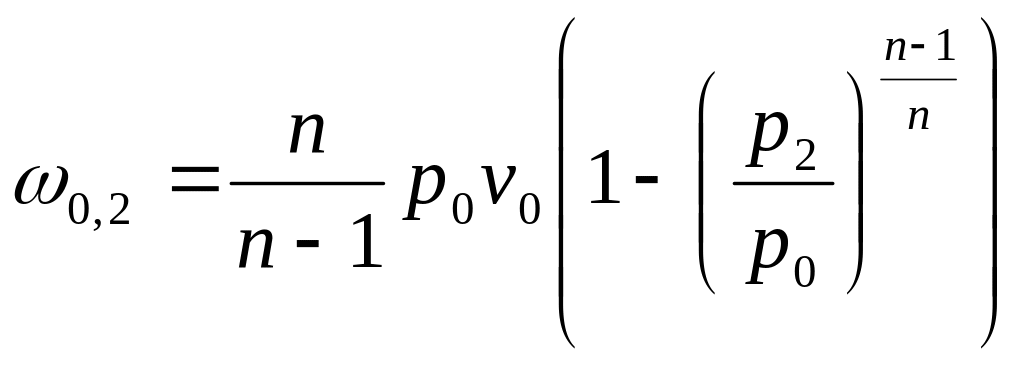. Подставив полученное выражение в уравнение для линейной скорости, получим: - уравнение линейной скорости для политропного процесса.

Уравнение линейной скорости для адиабатного процесса будет иметь следующий вид: .

В уравнение для массовой скорости входит плотность , которая меняется в течение процесса. Из уравнения политропного процесса можно получить уравнение для плотности: . Подставив полученное выражение уравнение для массовой скорости, получим: или - уравнение массовой скорости для политропного процесса.

Уравнение массовой скорости для адиабатного процесса будет иметь следующий вид: .

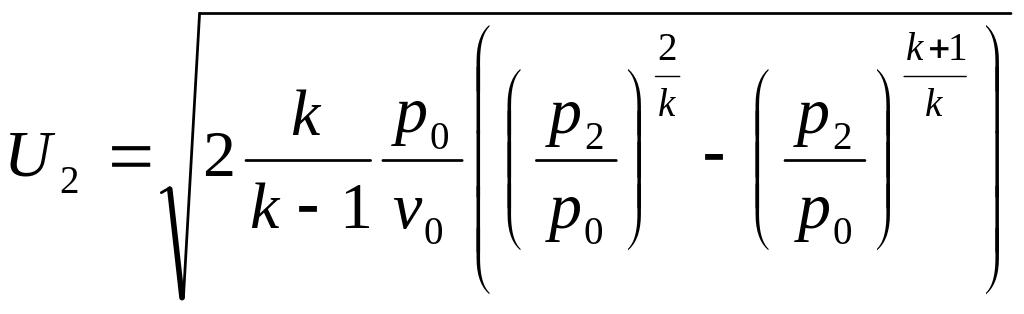Обычно отношение обозначают за . Коэффициент лежит в пределах от 0 до 1 .

Графическое представление зависимости линейной и массовой скоростей от отношения давлений.

В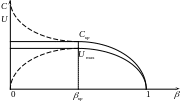 зависимости от соотношений давлений возможны три режима:

1. До критический (дозвуковой) режим - .

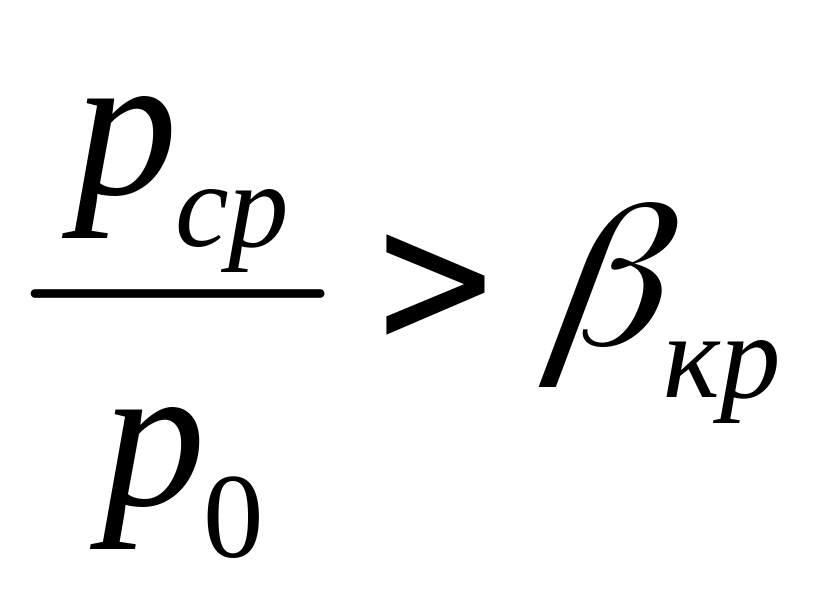2. Критический (звуковой) режим - .

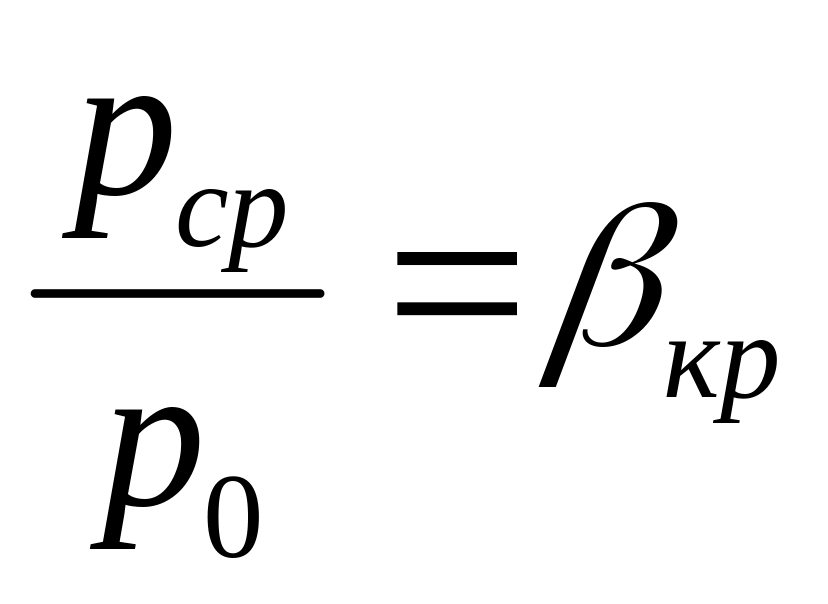3. За критический (сверхзвуковой) режим - .

Для определения режима нужно знать значение . Для этого нужно найти экстремумы функции . То есть , при .

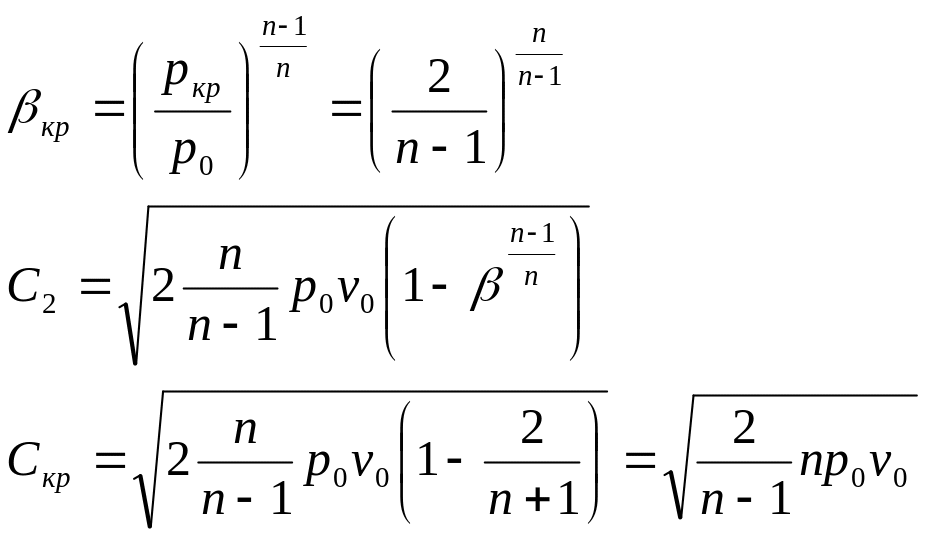
Характеристика растяжения сжатия:

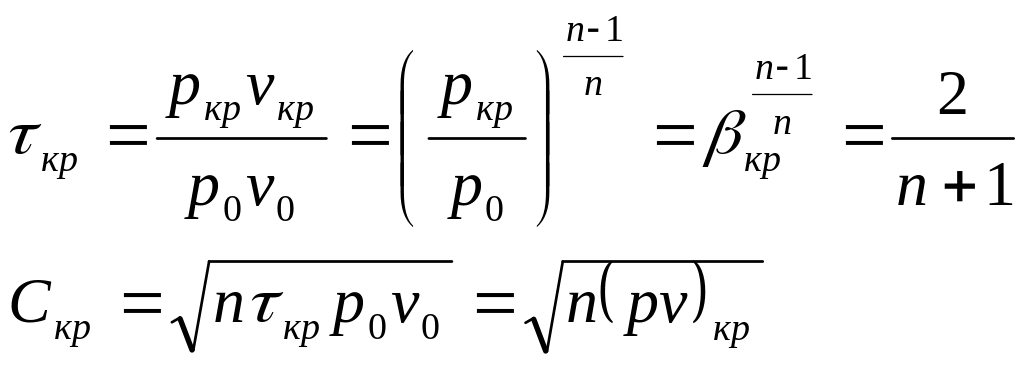
Для адиабатного процесса: , где - скорость звука.

Для идеального газа: .

Чтобы массовая скорость стала критической, то есть .

Массовый расход: .

Вопрос №25.