2.3. Доверительные границы при экспоненциальном распределении

Пусть при n опытах получен ряд значений x₁, x₂,...,x_i,...,x_n, тогда оценка среднего значения показателя x' может быть определена по формуле

,

нижняя доверительная граница показателя X_н - по формуле

(1)

а верхняя доверительная граница показателя X_в - по формуле

(2)

где коэффициенты доверительных границ R₁ и R₃ определяются из таблицы 2 (при заданном числе опытов n и заданной доверительной вероятности P. Обычно задаются значением Р = 0.9...0.95).

Тогда статистическое значение показателя Х может быть представлено в следующем виде:

X = X_H... X_B.

2.4. Анализ параметров методом доверительных интервалов

Метод применяется главным образом для оценки результатов эксплуатации или испытаний группы изделий, когда в нормативах заданы, например, минимально допустимая наработка на отказ T_доп, максимально допустимое количество отка­зов М_доп, максимально допустимая интенсивность отказов λ_доп или какой либо иной показатель надежности.

Ожидаемое значение наработки на отказ Т_о или ожидаемое значение отказов М_о (или λ_о) неизвестно, однако при этом должен быть известен закон распределения отказов.

Сущность метода заключается в том, что по результатам проводимых испы­таний определяется средняя величина (Т' или М' или λ'). Затем, по коэффициен­там, определяемым для заданной доверительной вероятности и соответствующего закона распределения (табл. 1, 2), вычисляются нижняя и верхняя доверитель­ные границы соответствующего показателя (например, Т_н и Т_в), после чего прово­дится анализ взаимного положения доверительных границ и норматива.

При этом возможны три случая:

1. Если Т_н ≥ Т_доп или М_н ≤ М_доп или λ_н ≤ λ_доп - требования нормативов под­тверждены.

При М ≠ 0 (отказы есть) доверительные границы Т_н и Т_в , М_н и М_в , λ_н и λ_в определяются по формулам (1, 2).

При М = 0 (отказов нет) верхняя доверительная граница Т_в не определяется, а нижняя доверительная граница Т_н определяется по формуле

,

где Т_СУМ - суммарная наработка всех n изделий, определяемая по формуле

,

t_i - наработка i-го изделия; R_o - коэффициент определяемый по таблице 2;

2. Если Т_в < Т_доп или М_в > М_доп , или λ_в > λ_доп - требования нормативов не под­тверждены.

3. Если Т_н < Т_доп < Т_в или М_н > М_доп > М_в или λ_н > λ_доп> λ_в - информации для определенного вывода (первый или второй случаи) недостаточно. Накопление данных по эксплуатации или испытанию изделий необходимо продолжить.

Расчет среднего значения соответствующего показателя надежности по имею­щимся результатам эксплуатации (испытаний) выполняется по формуле сред­него арифметического. Например, для средней наработки на отказ Т ' формула имеет вид

,

где n - количество наблюдаемых изделий;

На рис.6 представлена графическая иллюстрация метода оценки надежности по результатам эксплуатации (испытаний) методом доверительных интервалов.

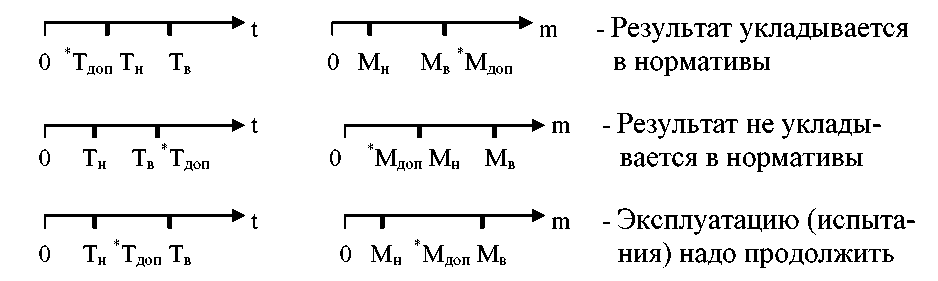
Рис. 6. Варианты взаимного расположение норматива и доверительных границ

Обозначения:

T_доп - минимально допустимая наработка на отказ;

Т_н (Т_в) - нижняя (верхняя) доверительная граница наработки на отказ;

М_доп - максимально допустимое число отказов;

М_н (М_в) - нижняя (верхняя) доверительная граница числа отказов.