1. Постановка задачі

1.1 Конформне відображення розрізаної двозв’язної кільцевої області з фіксованим розрізом.

Нехай в комплексній області Z площини X0Y задана двозв’язна кільцева область, обмежена двова кусково-гладенькими контурами , які задаються аналітично

а) явно:

б) неявно:

в) параметрично:

або точково (густими таблицями точок на контурах).

Нехай в такій двозв’язній кільцевій області проведено нескінченно тонкий фіксований розріз, що з’єднує два контури . Необхідно розрахувати чисельне конформне відображення так розрізаної двозв’язної кільцевої області на параметричний прямокутник площини . Іншими словами, необхідно знайти аналітичну функцію

(4.1)

або

(4.2)

(4.1) здійснює пряме відображення,

(4.2) – обернене.

Математична постановка даної задачі аналогічна до математичної постановки задачі відображення криволінійного чотирикутника. Алгоритм побудови чисельного конформного відображення аналогічний.

1.2 Конформне відображення розрізаної двозв’язної кільцевої області з вільним розрізом.

Аналогічна постановці 1.1 з тією різницею, що контур є вільним з двома фіксованими точками.

2. Математична постановка прямої задачі

Дійсна і уявна частини аналітичної функції (4.1) зв’язані умовою Коші-Рімана:

(4.3)

Граничні умови:

(4.4)-(4.5)

Рівняння контурів:

(4.6)

Розріз не задано, точки є «подвійними»:

(4.7)

Умови ортогональності ліній сітки її межам:

(4.8)

або:

(4.9)

Т.ч. (4.3)-(4.8) являють собою постановку прямої задачі чисельного конформного відображення розрізаної двозв’язної кільцевої області з вільним розрізом.

3. Математична постановка оберненої задачі

Рівняння контурів:

(4.10)

Умова «подвійності» точок розрізу

(4.11)

Умова ортогональності

(4.12)

або

Необхідно розрахувати:

1. координати вузлів вільного розрізу

2. координати плаваючих вузлів по контурах

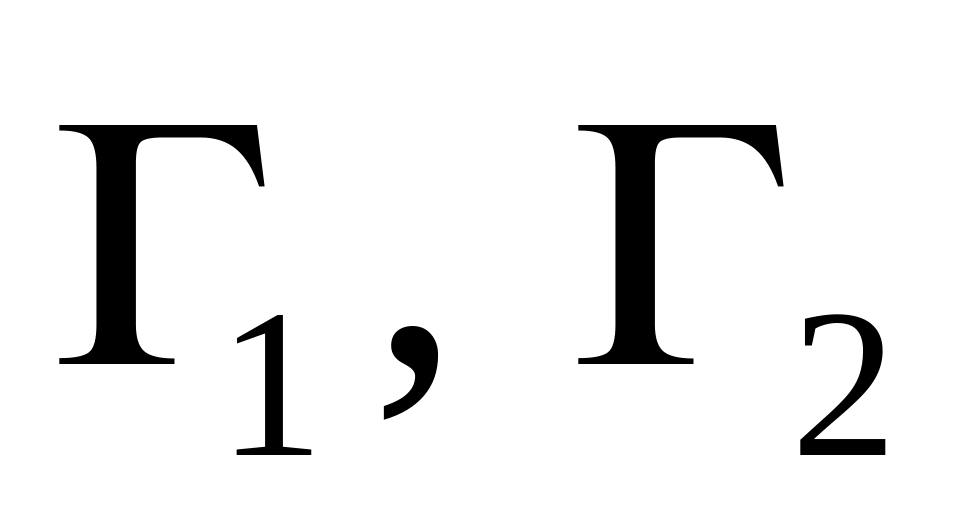
3. координати внутрішніх вузлів

4. знайти модуль області M або невідоме b.

4. Різницева схема задачі

(4.13)-(4.14)

- різницевий оператор Лапласа для математичної моделі, або оператор що апроксимує

(див. алгоритм 2)

(4.15)-(4.16)

(4.17)

Крім того на вільному розрізі виконується умова періодичності:

(4.18)

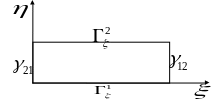
Біля меж виконуються умови ортогональності:

(*)

Дискретизувавши (*) біля , замінивши центральною різницею, а - уточненою, отримаємо:

(4.19)

Аналогічно для

(4.20)

Зауваження: замість (4.19)-(4.20), які отримали з дискретизації умов ортогональності (*) можна записати дискретні умови:

(4.19.1)

(4.20.1)

Можна використовувати додаткові умови зв’язку іншого типу, оскільки ці умови не використовують рівняння самої межі. Наприклад, можна застосувати рівняння:

або

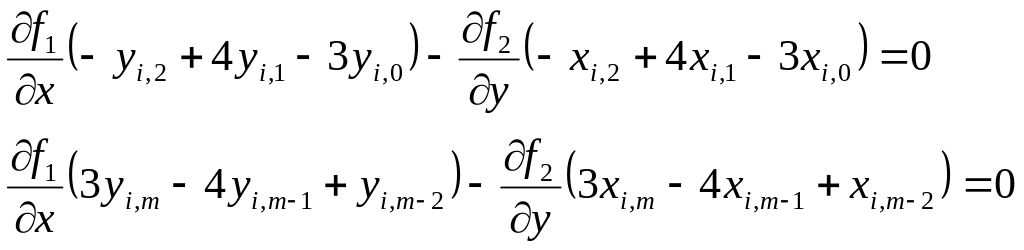(4.20.2)

Зауваження: для визначення координат плаваючих вузлів по поступаємо наступним чином:

одна з координат визначається з рівняння цього контура, а інша – з однієї з дискретизованих умов (4.19)-(4.20.2).

Наприклад, припустимо, що контур -коло радіуса

- визначили з рівняння меж

визначаємо з (4.19)-(4.20.2)

25