Вступ

При розв’язуванні крайових задач математичної фізики ми використовували різні методи, зокрема:

• метод сіток

• метод скінченних елементів

• метод граничних елементів

• метод радіальних базисних функцій

та інші.

Однією з причин, що ускладнює розробку алгоритмів розв’язку крайової задачі тим чи іншим методом, є наявність криволінійної межі розглядуваної області. Як правило, при розв’язуванні науково-технічних задач досить часто нас цікавить розв’язок задачі саме в околі межі цієї області. Один з методів чисельного розв’язування крайових задач, що враховують вплив криволінійних меж, є числовий метод конформних і квазіконформних відображень.

Чисельне конформне відображення використовується коли криво лінійна сітка є рівномірною. Квазіконформне ­­– з метою управління криволінійною системою координат, викликає локальні згущення в околі межі розглядуваної області або в окремих її під областях.

Розділ I

Автоматизація побудови різницевих сіток на криволінійних чотирикутниках з фіксованими межами за допомогою чисельних конформних відображень.

Тема 1

Постановка задачі чисельного конформного відображення криволінійного чотирикутника на параметричний прямокутник

1. Основні поняття та означення

Нехай G – чотирикутна область (криволінійний чотирикутник) на площині X0Y.

Під чотирикутною областю будемо розуміти будь-яку однозв’язну область обмежену кусково-гладкою управляючою кривою з чотирма фіксованими точками A,B,C,D, які при конформному відображенні даної області відображаються у вершини прямокутника.

Конформне відображення області – взаємно однозначне і неперервне відображення однієї області на іншу, яке зберігає сталість розтягу в кожній точці і консерватизм кутів, дійсна і уявна частини якого задовольняють умовам Коші-Рімана (C-R).

Якщо відображення здійснюється аналітичною функцією , то повинні виконуватись умови Коші-Рімана:

Чисельне конформне відображення – конформне відображення однієї області на іншу, реалізоване чисельними методами (наприклад, методом скінченних елементів).

Модуль конформного відображення – конформний інваріант , за допомогою якого функція здійснює конформне відображення.

Канонічна область – одна з простих областей (прямокутник, круг), на яку здійснюється конформне відображення заданої області.

Параметричний прямокутник – одна з канонічних областей, на яку здійснюється конформне відображення криволінійного чотирикутника.

Конформна різницева сітка - різницева сітка, отримана шляхом генерації за допомогою чисельного конформного відображення.

Гідродинамічна різницева сітка – різницева сітка, яка має гідродинамічний зміст, а саме: являє собою сукупність двох сімейств ліній, які є ізолініями деякого гідродинамічного поля (теплового, електростатичного).

2. Постановка задачі чисельного конформного відображення криволінійного чотирикутника на параметричний прямокутник

Нехай необхідно конформно відобразити чотирикутну область G площини так, щоб відмічені точки чотирикутника перейшли у відповідні вершини прямокутника.

При цьому відображення встановлює взаємно однозначну відповідність між межовими точками прямокутників і та між внутрішніми точками цих областей.

Нехай це відображення реалізоване аналітичною функцією

(1.1)

Тоді обернене відображення також реалізується аналітичною функцією

(1.2)

Координати точок областей і зв’язані умовами Коші-Рімана:

(1.3)

На сторонах параметричного прямокутника функції та задовольняють умовам:

(1.4)

До граничних умов (1.4) необхідно додати ще «рівняння зв’язку» межових точок області з примежовими в одному з виглядів:

1. умови Коші-Рімана: (1.5)

2. умови ортогональності ліній сітки області її межам, які не використовують функції самої межі: (1.6)

або

для (1.7)

для

Таким чином, нами сформульована математична модель прямої задачі чисельного конформного відображення криволінійного чотирикутника на параметричний прямокутник.

3. Математична модель задачі конформного відображення в оберненій постановці

Будемо шукати обернене конформне відображення прямокутника на криволінійний чотирикутник . Обернене відображення представлене функцією , і також є конформним, тобто функції

задовольняють умовам Коші-Рімана.

На ділянках границі спряжені гармонічні функції зв’язані рівняннями межі:

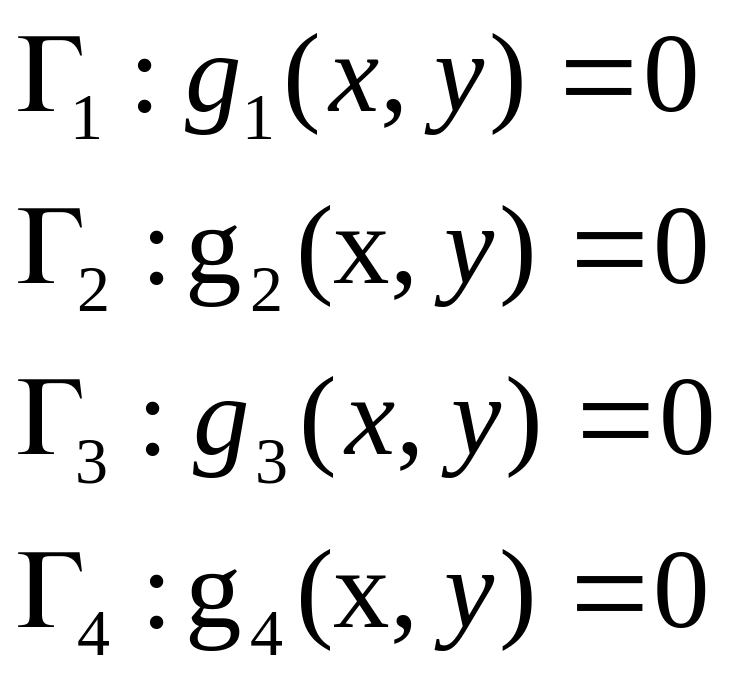
(1.8)

Тоді задача побудови оберненого конформного відображення полягає в тому, щоб знайти пару спражених гармонічних функцій (зв’язаних умовами Коші-Рімана), що задовольняють рівнянням границь:

До граничних умов необхідно додати ще рівняння зв’язку межових точок з примежовими в одному з виглядів:

1. умови Коші-Рімана 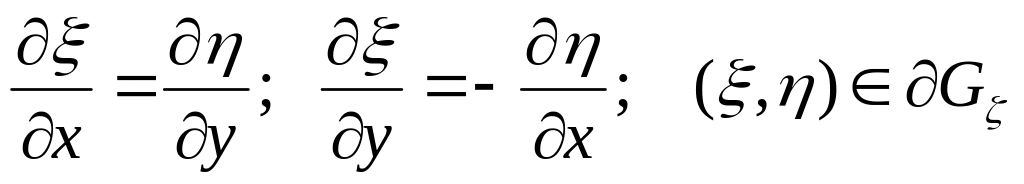(1.9)

2. умови ортогональності ліній сітки області її межам

   1. які не використовують рівняння самої межі

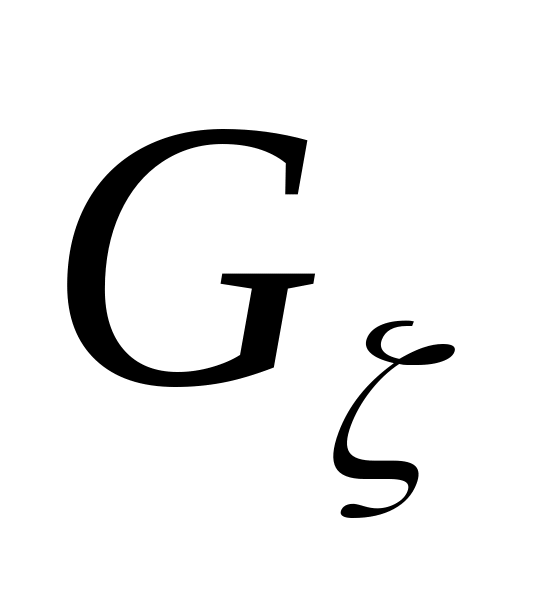
або (1.10)

2. які використовують рівняння межі

для (1.11)

для

або в розгорнутому вигляді:

(1.12)

Алгоритм побудови різницевих сіток за допомогою даної математичної моделі ґрунтується на апроксимації системи рівнянь Коші-Рімана.