Построение одновыходных схем. Декомпозиция булевых функций.

Задача декомпозиции булевой функции в общем случае состоит в таком разделении множества ее аргументов на ряд подмножеств, при котором можно выразить исходную функцию f(x) через вспомогательную промежуточную функцию j(z), где zÌx.

В частном случае имеет место так называемая простая разделительная декомпозиция, при которой множество аргументов x разделяется на два непересекающихся подмножества (z,w®(zÇw=j;zÈw=x)) и приведение исходной функции к виду f(x)=f(j(z,w)).

Пример : f³(x)=V(1,2,4,7)

(f=1)

z=(x₂x₃) W={x₁}

j(z)= `x<sub>2</sub>x<sub>3</sub>vx<sub>2</sub>`x₃

f(x)= `x<sub>1</sub>j(z)vx<sub>1</sub>`j(z) S_Q=13

S_Q=13 T=5t

Схема базиса Жигалкина.

S_Q=4 T=2t

Применение декомпозиции там, где он уместно, во многих случаях позволяет уменьшить цену синтезируемой схемы.

МДНФ y=x₁`x<sub>2</sub>x<sub>3</sub>`x₄vx₂`x<sub>5</sub>v`x₃`x<sub>5</sub>vx<sub>4</sub>`x₅=x₁`x<sub>2</sub>x<sub>3</sub>`x₄v`x<sub>5</sub>(x<sub>2</sub>v`x₃vx₄)

S_Q=14

j(z)=x₂v`x₃vx₄

___ _

f(x)=x₁*y(z)vx₅*j(z) S_Q=10

Синтез многовыходных комбинационных схем.

МКС представляется в виде обобщенного «черного ящика»

Закон функционирования МКС представляется в виде системы булевых функций

|y₁=f₁(x₁...x_n)

|y₂=f₂

|.

|.

|.

|y_n=f_n

Естественным образом, при решении задачи синтеза МКС применяются методы факторизации и возможной декомпозиции, применительно не к одной функции, а к системе.

Минимизация системы Булевых функций

Задача минимизации применительно к системе Булевых функций решается аналогично как для одной функции и сводится к получению минимального покрытия. Для решения этой задачи система приводится к одной функции путем дополнения множества агументов подмножеством вспомогательных переменных, с помощью которых выделяются отдельные функции системы. Количество вспомогательных переменных k³log₂m, m - количество функций.

Пример:

Раздельная минимизация:

y₁ Cmin (y₁)=

y₂ Cmin (y₂)=

МДНФ:

При построении схемы по этому выражению, она разлагается на две независимые подсхемы, отдельные для реализаций каждой функции.

Совместная минимизация

Пусть V=0 для у₁; V=1 для y₂

Cmin(y₁,y₂)=;

Z= (общий терм)

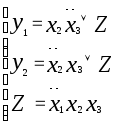
Пример:

V₁V₂=00 y₁

V₁V₂=01 y₂

V₁V₂=10 y₃

V₁V₂=11 y₄

Cmin(S)=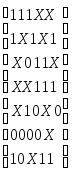

Общие термы:

При совместной минимизации Булевых функций система в минимальной форме может оказаться, что некоторые термы поглощаются другими, т.е. после получения минимальной формы необходимо исключить поглощаемые термы.

После получения минимального покрытия при записи минимальных форм с начала выделяются термы, общие для нескольких функций и обозначаются вспомогательными функциями (Z₁-Z₄).

В целях удобства рядом с каждым общим термом рекоммендуется проставить его принадлежность.

Далее выписываются минимальные формы для отдельных функций с учетом их собственных термов и общих термов, принадлежащих данной функции. При наличии незадействованных комбинаций вспомогательных переменных все наборы аргументов для них являются безразличными.

Пример:

Сmin(S)=

Для большого числа функций и их аргументов применение карт Карно для совместной минимизации выглядит затруднительным. В этом случае можно использовать следующие подходы:

1. Применение машинных методов

2. Раздельная минимизация и использование карт Карно.

3. Выделение подмножеств из функций системы для их совместной минимизации.