3.3. Геометрическая интерпретация задачи линейной оптимизации

Задана математическая модель:

, (3.19)

(3.20)

, . (3.21)

Каждое из неравенств системы ограничений (3.20) и (3.21) является полупространством с граничными гиперплоскостями

, ( ),

, ( .

Пересечение полупространств, заданных системой ограничений, если она совместна, будет выпуклым многогранником, который образует область допустимых решений (ОДР) системы ограничений.

Любая внутренняя и граничная точка ОДР является решением задачи. Приравняем функцию (3.19) к нулю, тогда уравнение

представляет собой гиперплоскость, проходящую через начало координат и перпендикулярную вектору-градиенту. Направление вектора-градиента показывает направление возрастания функции. Поэтому, чтобы найти максимум функции, нужно передвигать гиперплоскость в направлении вектора как можно дальше от начала координат, но чтобы она имела с ОДР хотя бы одну общую точку. Чтобы найти минимум функции, нужно определить ближайшую точку в ОДР от начала координат.

Для двумерного пространства на рис. 3.1 показано, что в угловой точке А максимальное значение функции, а в точке В - минимальное.

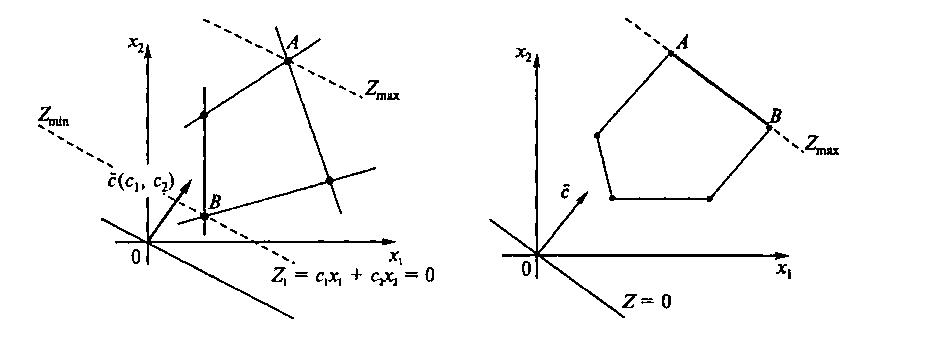
Рис.3.1. Область допустимых решений задачи с максимальным и минимальным значениями в угловых точках

Рис. 3.2. Область допустимых решений задачи с множеством решений

Рис. 3.2 отражает случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции 2 достигается в точке А и в точке В, следовательно, и в любой точке отрезка АВ, так как эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.

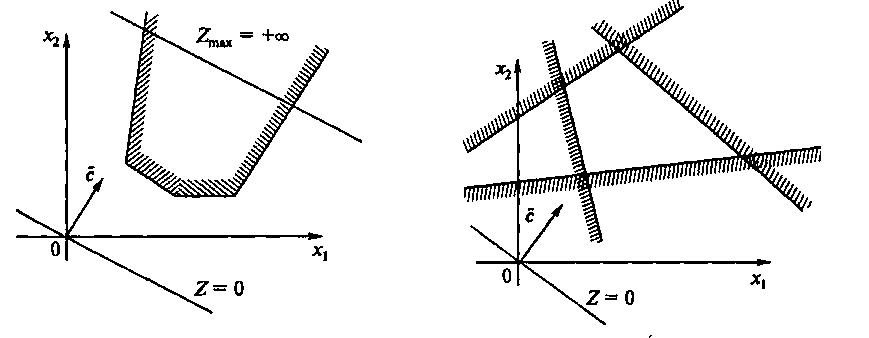
Рис. 3.3. Множество, неограниченное сверху

На рис. 3.3 изображен вариант, когда система ограничений образует неограниченное сверху множество. Функция z при этом стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко.

На рис. 3.4 представлен случай несовместной системы ограничений.

Рис. 3.4. Несовместная система ограничений

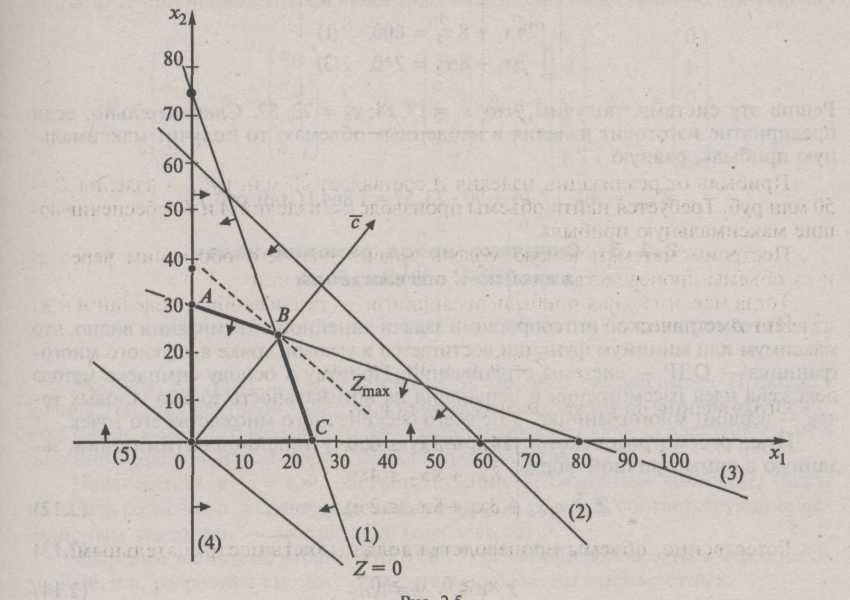
Пример решения лабораторной работы №1

Задание. Построить на плоскости область решений линейных неравенств

и геометрически найти максимальное и минимальное значения целевой функции в этой области. (Все решения должны быть неотрицательными, т.е. , ).

Решение.

Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений-неравенств запишем в виде уравнений и пронумеруем их:

Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: при =0, =75, а при =0, =25. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем любую точку на плоскости, не лежащую на прямой, например, точку и подставим ее координаты в неравенство - оно является верным. Так как точка О(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой 24 +8 =600. На рисунке расположение полуплоскости относительно первой прямой отмечено стрелками.

Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенствам. Точки, удовлетворяющие ограничениям , , находятся в первом квадранте.

Множество точек, удовлетворяющих всем ограничениям одновременно, является областью допустимых решений системы ограничений. На графике это многоугольник ОАВС.