4.4.2. Транспортная задача
Пример 4.3. Рассмотрим применение информационных технологий Excel для решения транспортной задачи на примере, представленном в таблице 4.2.
Таблица 4.2. Исходные данные для транспортной задачи
Поставщики |
Потребители |
Запас |
|||
1 |
2 |
3 |
4 |
||
1 |
4
|
2
|
3
|
0
|
500 |
2 |
3
|
1
|
6
|
0
|
600 |
3 |
2
|
7
|
8
|
0
|
700 |
4 |
1
|
9
|
4
|
0
|
800 |
Спрос |
900 |
400 |
450 |
850 |
2600 2600 |
Введем данные в компьютер в виде, показанном на рис. 4.13.
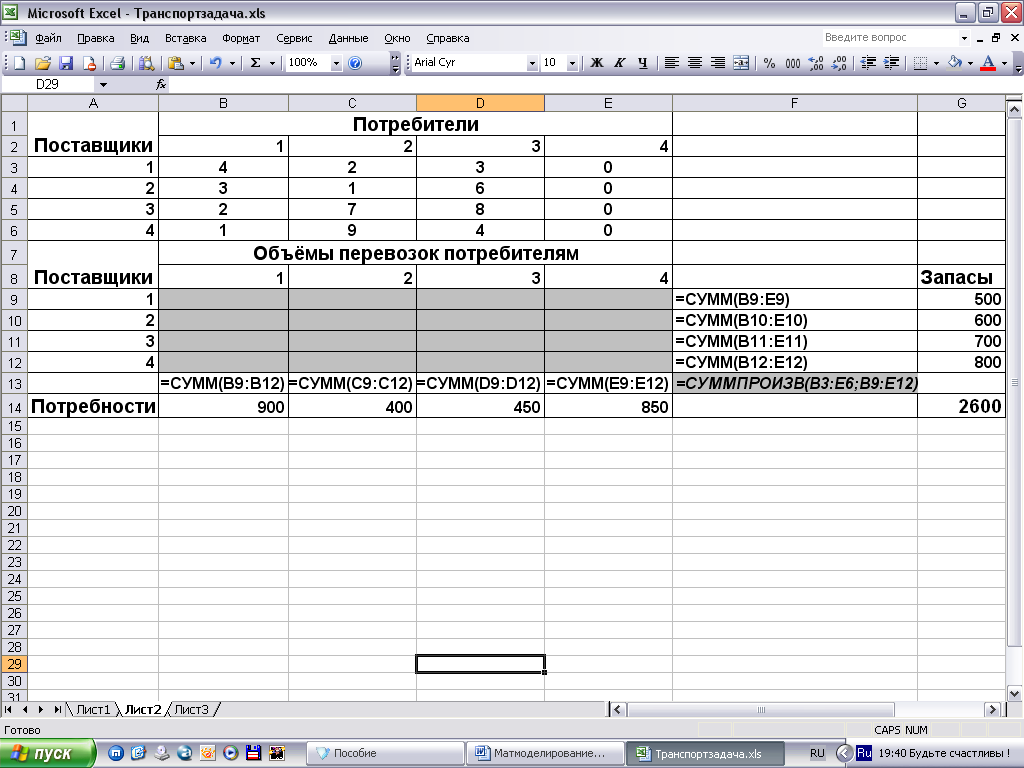
Рис. 4.13. Рабочий лист транспортной задачи 4.4
В массив В3:Е6
введены значения стоимости перевозок
единицы груза. В ячейки В14:Е14 введены
величины спроса потребителей, в G9:G12
- запасов поставщиков, а в ячейку G14
– суммарного запаса, равного суммарному
спросу и составляющего 2600 единиц. Массив
В9:Е12 отведен под значения неизвестных
(объемы перевозок), где i=1,2,3,4;
j=1,2,3,4.
Функция =СУММПРОИЗВ(В3:Е6;В9:Е12) введена
в ячейку F13.
Функция отражает сумму произведений
стоимости
на объемы
перевозок
.
В массивы F9:F12
и В13:Е13 введены левые части ограничений
задачи
(i=1,2,3,4)
и
(j=1,2,3,4)
соответственно. Эти суммы и целевая
функция введены с помощью Мастера
функций.
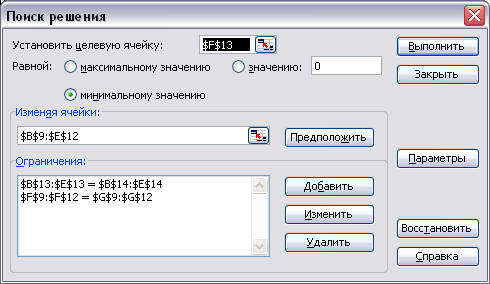
Рис.4.14. Диалоговое окно Поиск решения
После ввода данных вызывается диалоговое окно Поиск решения. В этом диалоговом окне заносится номер ячейки с целевой функцией (F13), номера изменяемых ячеек (В9:Е12), устанавливается направление оптимизации, а также вводятся ограничения (рис. 4.14):
$B$13:$E$13=$B$14:$E$14, $F$9:$F$12=$G$9:$G$12.
В диалоговом окне Параметры поиска решения установим флажок Линейная модель, Неотрицательные значения (рис. 4.6) и, щелкнув по кнопке ОК, возвратимся в диалоговое окно Поиск решения. Щелкнув левой кнопкой мыши по кнопке Выполнить в этом окне, получим на экране результат решения задачи (рис. 4.15).
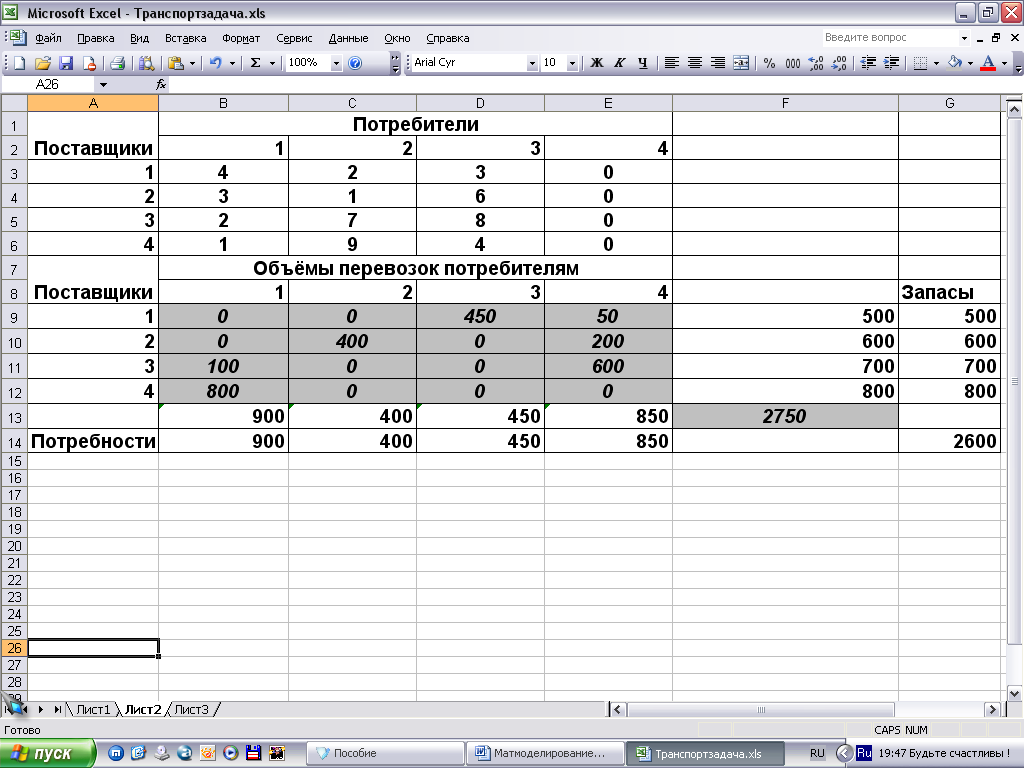
Рис. 4.15. Оптимальное решение транспортной задачи 4.3
Таким образом,
=2750,
=450,
=50,
=400,
=200,
=100,
=600,
=800.
Остальные объемы перевозок груза равны
нулю.
Если оптимальное решение не найдено
Если надстройка Поиск решения прекратила работу не найдя оптимального решения, то причинами этого могут быть:
процесс поиска решения был прерван пользователем;
в диалоговом окне Параметры поиска решения установлен флажок Показывать результаты итераций;
пользователь нажал кнопку Стоп в режиме пошагового выполнения итераций;
количество итераций или время поиска решения превысило максимально допустимое;
при решении нелинейной задачи в диалоговом окне Параметры поиска решения установлен флажок Линейная модель;
значение целевой ячейки неограниченно возрастало или убывало;
при использовании условия целочисленности задано слишком маленькое Допустимое отклонение (параметр в диалоговом окне Параметры поиска решения;
при решении нелинейной задачи с медленной сходимостью параметр Сходимость в диалоговом окне Параметры поиска решения имеет слишком большое значение;
модель включает переменные, значения которых отличаются на несколько порядков, и при этом флажок Автоматическое масштабирование в диалоговом окне Параметры поиска решения не включен.