Задача № 8.

Определить расход воды в трубопроводе диаметром d₁ при помощи водомера Вентури, если диаметр горловины d₂ и разность показаний пьезометров h (рис. 8).Температура воды t.

1

1

2

2

0

0

Ось трубы

Рис. 8

Д ано: Решение:

h = 470 мм; Составим уравнение Бернулли для сечений 1-1 и 2-2, принимая

t = 32 ^oC; за плоскость сравнения ось трубы:

d₁ = 320 мм;

d₂ = 160 мм; ;

Учитывая, что z₁ = z₂ = 0, пренебрегая в первом приближении

Найти: потерями напора, т.е. принимая = 0 и полагая α₁ = α₂ = 1;

V - ? получим:

;

Из уравнения неразрывности (постоянства расхода) течения имеем: V = S₁·υ₁ = S₂·υ₂;

т.к. , а , то ;

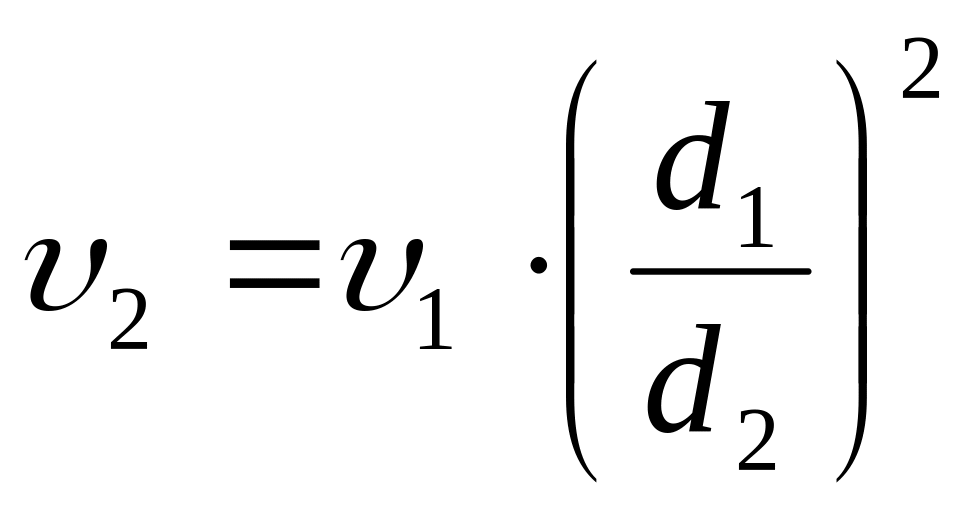Обозначим: , тогда уравнение Бернулли запишется в виде:

;

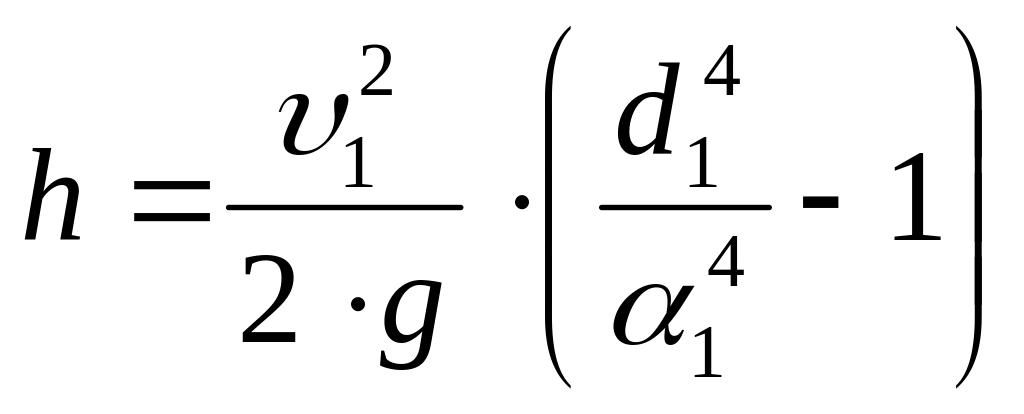Откуда:

;

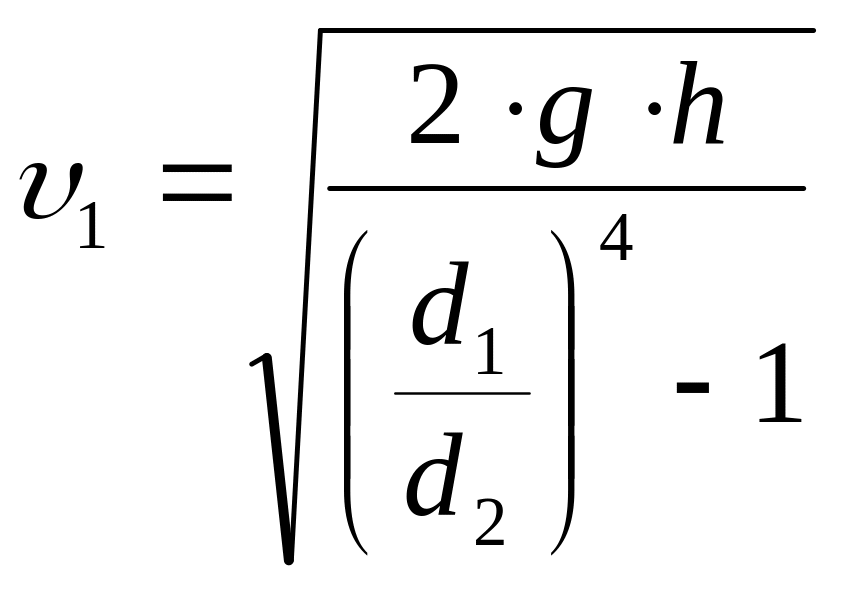Тогда расход воды в трубе:

;

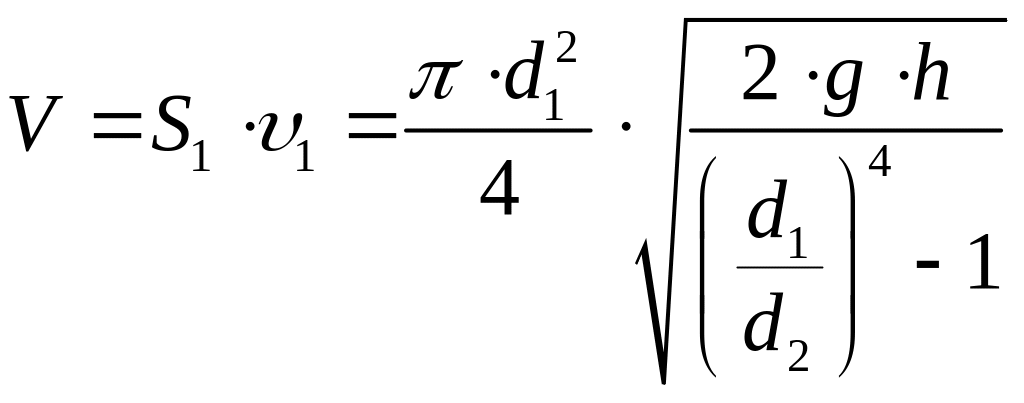Но так как мы пренебрегли потерями напора, то расход воды будет меньше. С учетом этих потерь формула для определения расхода запишется в виде:

μ· ;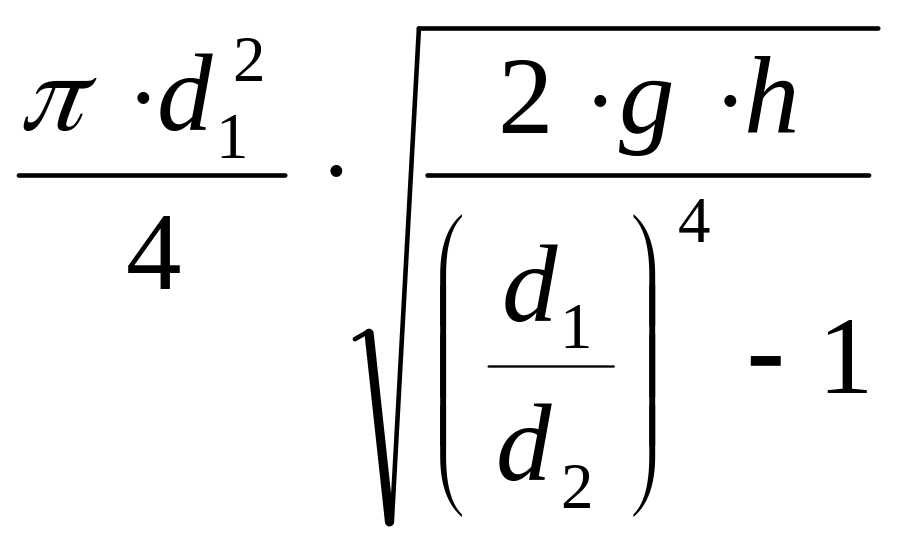

где μ – коэффициент, учитывающий уменьшение расхода вследствие потерь напора.

Примем μ = 0,98

тогда:

0.0618 м³/с;

μ зависит от и числа Рейнольдса (по приложению 13 с.233 «Примеры расчетов по

гидравлике» под ред. Альтшуля, 1976 г.)

=0,5;

Re = ;

Скорость в сужении трубы: м/с;

Кинематическую вязкость воды находим по прил.2 для t = 32 ^оС, ν = 0,81·10^-6 м²/с;

Тогда Re = 607407.4 > 2320 (значит режим турбулентный)

Ответ: V = 0,0618 м³/с.

Задача № 9.

Сифонный бетонный водосброс внешним диаметром d общей длиной l сбрасывает воду из водохранилища в реку, уровень которой на Н ниже уровня водохранилища (рис. 9). Определить подачу сифонного водосброса, если он имеет два поворота: ₁ = 90⁰, ₂ с радиусами закругления R. Длина горизонтального участка l_г , толщина стенок водосброса δ. Температура воды в водохранилище t. Определить также вакуум в верхней точке сифона.

0

0

1

1

2

2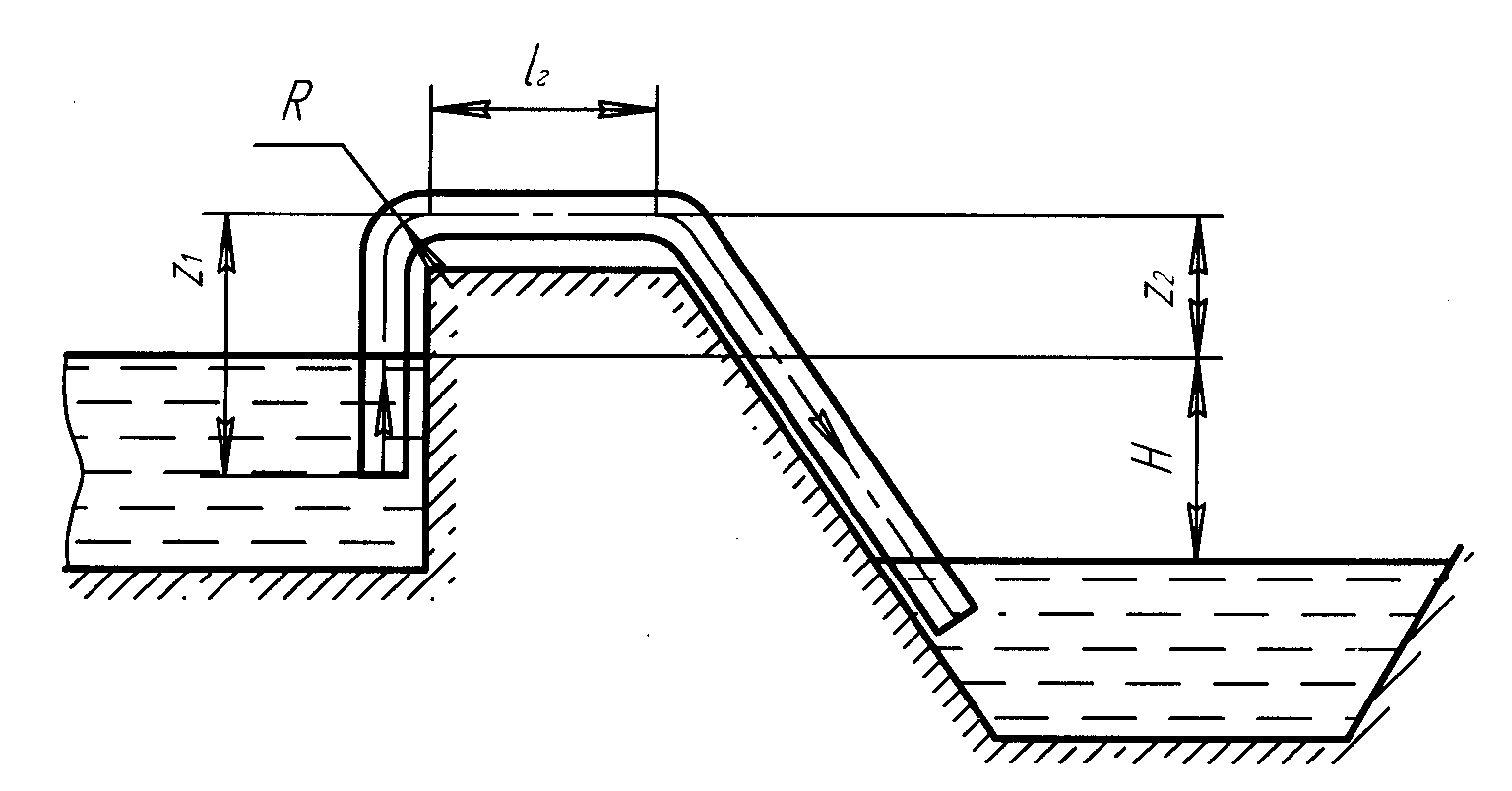

Рис. 9

Дано: d₁ = 0,6 м; H = 1,4 м; l = 45 м; l_г = 2,2 м; R = 2,3 м; α₂ = 40^o; δ = 30 мм; t = 20 ^oC; z₁ = 2,8 м; z₂ = 1,4 м;

Найти: V - ? P_вак - ?

Решение:

Разность уровней воды в водохранилище и реке определяет суммарные потери давления в сифонной трубе:

; где ;

Откуда скорость движения воды в сифоном водосбросе:

= ;

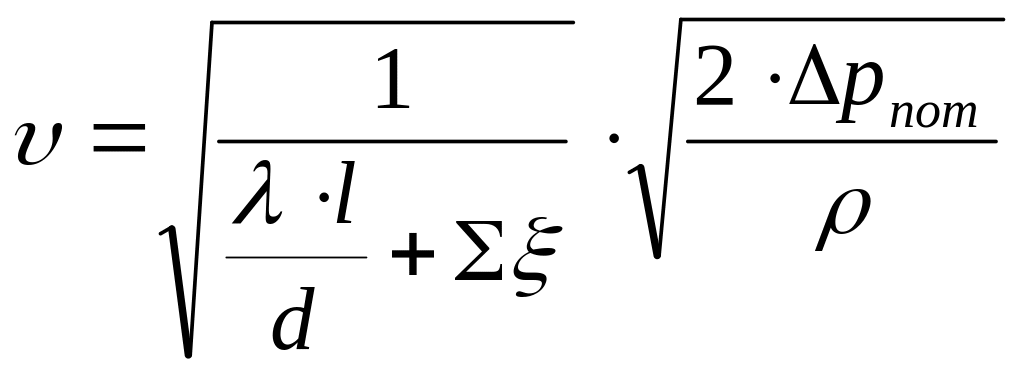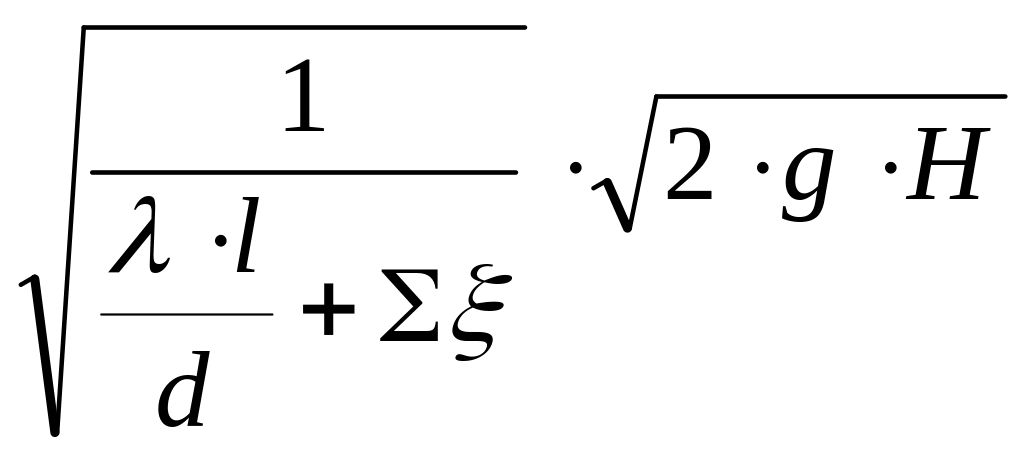Примем первоначально, что водосброс работает в квадратичной области сопротивления, тогда по формуле 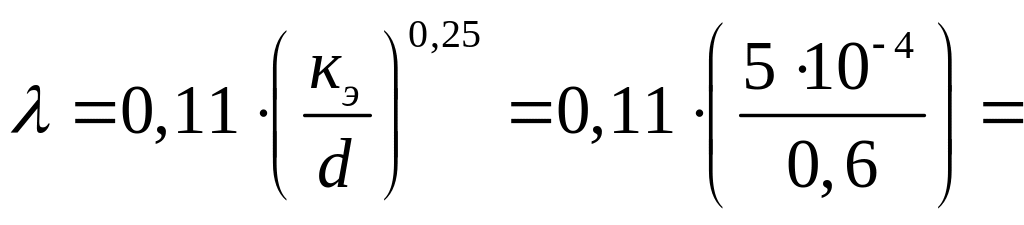0,019;

где к_э = 0,5 мм ( бетонная труба, б.у. по справочнику );

коэффициент местного сопротивления на вход в трубу ( при δ/d = 0,03/0,6 = 0,05 )

ξ_вх = 0,5;

коэффициент сопротивления на поворот 90^о находим по формуле А.Д.Альтшуля:

= 0,189;

коэффициент сопротивления на поворот α₂ = 35^о определяется по формуле:

ξ₃₅^о = ξ₉₀^о·а = 0,189·0,65 = 0,123 где а = 0,65 ( по приложению для α₂ = 35^о );

коэффициент сопротивления на выход из трубы: ξ_вых = 1;

тогда сумма коэффициентов местных сопротивлений:

Σξ = ξ_вх + ξ₉₀^о + ξ₃₅^о + ξ_вых = 0,5+0,189+0,123+1 = 1,8;

Тогда:

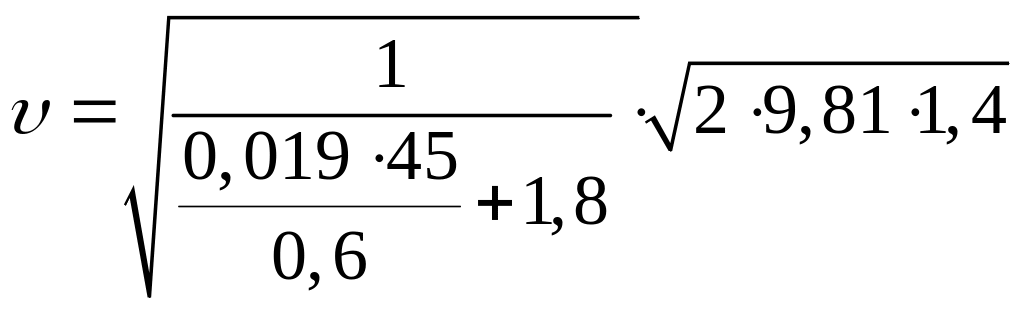= 2,91 м/с;

определим Re ( при ν = 1,01·10^-6 м²/с для температуры воды t = 20 ^oC );

Re = ;

При =8,3·10^-4 ( по рис.3.4. ( с.61 ) установили, что выброс работает в квадратичной области сопротивления );

Расход воды через сифонный водосброс:

V = 0,82 м³/с;

Составим уравнение Бернулли для сечения 1-1 и 2-2:

;

Потери напора на учатке 1-2:

Δр_пот^1-2 = ;

где l₁= z₂ + l₂ = 1,4 + 2,2 =3,6 м;

ρ = 998 кг/м³ ( для воды при t = 20 ^oC );

Δр_пот^1-2 = 0,33·10⁴ Па;

Величина вакуума в верхней точке водосброса:

р_вак = р₁ – р₂ = 996·9,81·2,8+996· +0,33·10⁴ = 34748,2 Па;

Ответ: V = 0,82 м³/с; р_вак = 34,75 к Па.