2. An Opening Address (a Model) Образец вступительной речи председателя на научной встрече

Chairman: Distinguished guests, ladies and gentlemen, clear colleagues! It is a great pleasure for me as Chairman of the Organizing Committee to welcome you to the International Symposium on Semiconductor Device Research sponsored by the Division of Chemical Physics of the American Physical Society. I would like to give a special welcome to the President of the American Physical Society, Professor Kenneth Johnson who has found the time to attend our meeting. I express our warmest welcome to the Assistant Director of the Massachusetts Institute of Technology, Professor Charles Stucky. I am sure you will join me in extending a particular welcome to our colleagues from other countries. We are pleased that so many outstanding researchers from all over the world have come to attend this Symposium. We would like to convey our best wishes to all the participants and guests. Two years have passed since our last meeting in Germany. It is a short time, but it has fumed out to be very fruitful There has been remarkable progress in our understanding of the device operation and some underlying phenomena. The most notable achievement is die discovery of room temperature superconductivity. It has brought about improvement in structure technology and in designing new devices and materials. However, our knowledge of the mechanism of superconductivity still remains incomplete. Our main goal in holding this Symposium is to discuss various aspects of new materials for semi- and superconductor structures. The range of subjects to be considered is quite large. But it is our hope that the Symposium will show the current state of things in this rapidly developing area and stimulate new ideas. Because the meeting has brought together scientists with different points of view, with different backgrounds of training and experience, we; expect stimulating discussions of theoretical and experimental problems. I wish you success. Thank you.

3. Mathematical Formulae Математические формулы

a equals b

a is equal to b

a plus or minus b

a plus b is с

a plus b equals с

a plus b is equal to с

a plus b makes с

four plus seven is eleven

four plus seven equals eleven

four plus seven is equal to eleven

с minus b is a

eighteen minus six is equal to twelve

eighteen minus six equals twelve

eighteen minus six is twelve

eighteen minus six leaves twelve

five times five is twenty five

five multiplied by five equals twenty five

five by five is equal twenty five

twelve is greater than five plus five

five plus five is less than twelve

a j-th

a sub j

a plus b all squared

a second is greater than a d-th

x tends to infinity

bracket two x minus у close the Bracket

(distance = velocity * time) S equals v by t

S is equal to v multiplied by t

S equals v times t, where S means distance,

v means velocity, t means time

(work = force * distance) work is equal to the product of the force multiplied by the distance

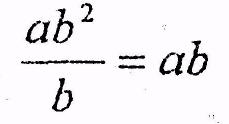ab square (divided) by b equals ab

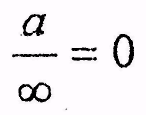a divided by infinity is infinitely small

a by infinity is equal to zero

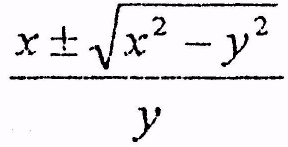x plus or minus square root of x square minus у square all over у

sixteen divided by four is four

sixteen by four equals four

sixteen by four is equal to four

the ratio of sixteen to four is four

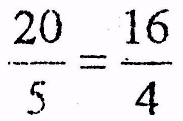the ratio of twenty to five equals (is equal to) the ratio of sixteen to four

the ratio of fifty one to one

two to three is as four to six

a (one) half

a (one) third

a (one) quarter; a (one) fourth

two thirds

a raised to the fifth power

a to the n-th power

the square root of a

у to the minus tenth power

the square root of sixteen is four

alpha equals the square root of capital R square plus x square

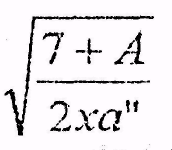the square root of 7 plus capital A divided by two x a double prime

dz over dx

the first derivative of z with respect to x

the second derivative of у with respect to x

d two у over d x square

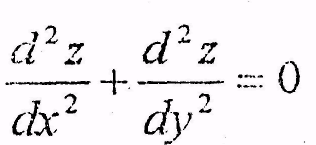partial d two x over partial dx² plus partial d two z over partial dy² equals zero

у is a function of x

the integral from n to m

integral between limits n and m

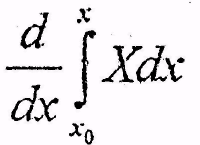d over dx of the integral from x nought to x of capital X dx

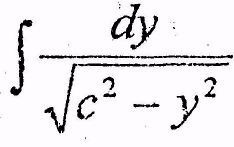the integral of dy divided by the square root out of с square minus у square

a cubed is equal to the logarithm of d to the base с

u is equal to the integral off sub one of x multiplied by dx plus the integral of f sub two of у multiplied by dy

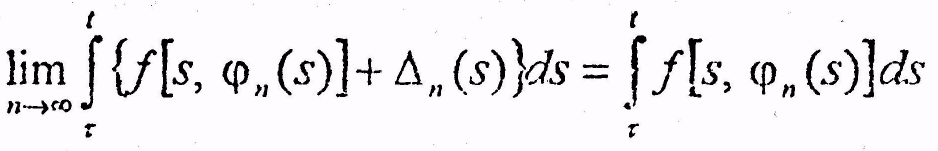
the limit as n becomes infinite of the integral of f of s and of s plus delta n of s, with respect to s, from to t, is equal to the integral of f of s and of s, with respect to s, from to t

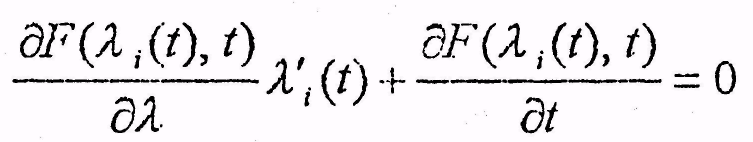
the partial derivative of F of lambda sub i of t and t, with respect to lambda, multiplied by lambda sub i prime of t, plus the partial derivative of F with arguments lambda sub i of t and t, with respect to t is equal to zero

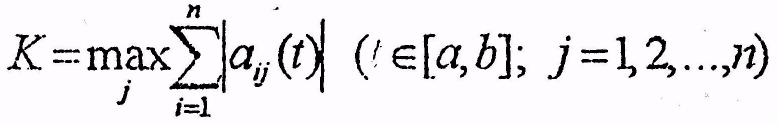
F is equal to the maximum over j of the sum from i equals one to i equals n of the modulus of of t, where t lies in the closed interval ab and where j runs from one to n