26. Классификатор для распознавания трёх классов образов по критерию наименьшего среднеквадратичного расстояния

Классификатор для распознавания трёх классов , работающий по критерию наименьшего среднеквадратичного расстояния можно представить иллюстративно следующим образом

Рис. 26.1

Определяем преобразование , отображающее 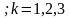в в смысле наименьших квадратов . Выберем в качестве вершины трёх единичных векторов , как показано на рис. Обозначим априорные вероятности классов через . Преобразование можно непосредственно найти из соотношения

Решая это уравнение относительно , получим

где (26.1)

(26.2)

Очевидно, что и являются матрицами взаимной корреляции и автокорреляции соответственно. Следует отметить, что матрица имеет размерность . Для классификации образа классификатор вычисляет в первую очередь 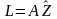, а затем отображает в пространство решений. При этом применяется следующее решающее правило по критерию минимума расстояния : если наиболее близко к , то классифицируется как принадлежащий . Расстояния , которые вычисляет классификатор определяются как

т.е.

Так как ,то будет минимально ,когда максимально. Поэтому вместо в последнем соотношении достаточно, чтобы классификатор вычислял

(26.3)

Подставляя и в (26.3) получаем

Матрица преобразования обозначается как

,

где представляют собой следующие дискриминантные функции , которые определяют классификатор

.

Из последнего соотношения следует , что классификатор полностью определяется матрицей преобразования , которая получается из множества обучающих образов.Для классификации данного образа классификатор вычисляет три числа , и .

Если то этот образ приписывается .

Рис. 26.2 Структура классификатора для трех классов

27. Классификатор для распознавания k классов образов по критерию наименьшего среднеквадратного расстояния

Задача трёх классов может быть обобщена для случая K классов. Расширенные образы, принадлежащие C_i отображаются в вершине единичного К-вектора V_i

_,

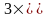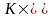где ненулевой элемент «1» находится в i-ой позиции V_{i ,} i= . Вместо матрицы преобразования A размерностью ( +1) получаем матрицу размерностью ( +1)

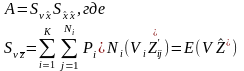
Таким образом, дискриминантные функции, определяющие классификатор, имеют вид

Рис. 27.1 Структура классификатора k классов

При обсуждении классификаторов по минимуму расстояния мы ограничивались рассмотрением только линейных классификаторов , т.е. классификаторов ,которые обладают линейными разделяющими границами в пространстве признаков. Соответствующую процедуру обучения нетрудно получить для случая квадратичных разделяющих границ, но при этом реализация классификатора усложняется. Квадратичный классификатор определяется дискриминантными функциями вида

(27.1)

Из последнего соотношения следует, что квадратичная дискриминантная функция имеет [( +1)/( +2)]/2 весовых коэффициентов или параметров, а именно:

параметров , соответствующих коэффициентам при

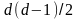параметров , соответствующих коэффициентам при

параметров, соответствующих коэффициентам при

порог-

Приведённые выше параметры определяются в процессе обучения .

Для пояснения реализации классификатора, связанного с вычислением (27.1) определим Q-мерный вектор G, координаты которого f₁,f₂,…,f_Q являются функциями z_i , 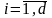. Первые координат вектора G имеют вид ,следующие координаты всем парам z₁z₂,z₁z₃,…, ; последние координат представляют собой z_1,z_2,…, .

Тогда реализация классификатора будет иметь вид

Рис. 27.2