23. Структура системы распознавания образов с применением ортогональных преобразований. Принцип обучения в двухклассовой системе распознавания
Систему распознавания образов с применением ортогональных преобразований можно представить в виде
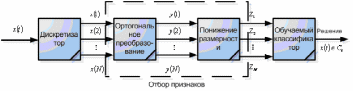
Рис. 23.1
Через
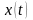обозначается сигнал , принадлежащий
одному из
классов
.
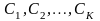На первом этапе
выбора осуществляется ортогональное
преобразование. Вторым этапом выбора
признака является понижение размерности,
после чего получаем подмножество
признаков
из
причём
.
Понижать размерность следует таким образом , чтобы сопутствующее этому увеличение ошибки классификации было относительно невелико. Классификатор, изображенный на рис. 23.1 является решающим устройством, которое обучается с целью классификации входного сигнала , принадлежащего к одному из классов.
Принцип обучения
наилучшим образом можно объяснить с
помощью простого примера. Предположим,
что мы желаем обучить классификатор
автоматически классифицировать образ
,
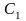принадлежащий либо классу
,
либо классу
.Предположим также что обучающее
множество (т.е. множество истинная
классификация которого известна) состоит
из следующего множества двумерных
образов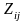
, где
обозначает
-ый
образ , принадлежащий
Образы
, принадлежащие классам
и
,
располагаются в двумерном пространстве
признаков , как показано на рис. 23.2
Рис. 23.2
Пусть
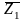и
- средние векторы образов , связанные с
и
соответственно. Тогда
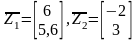(23.1)
Из рис. 23.2 видно, что наиболее целесообразной решающей границей (т.е. линией на плоскости ), разделяющей классы и , является срединный перпендикуляр к прямой, соединяющей и . Следующим шагом является описание решающей границы с помощью уравнения.
Рассмотрим любую точку , принадлежащую решающей границе, как показано на рис. Так как решающая граница является срединным перпендикуляром к прямой , соединяющей и , то
или в упрощенном
виде
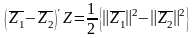(23.2)
Подставляя (23.1) в (23.2), получим уравнение для решающей границы в виде
(23.3)
Величина
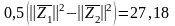называется порогом классификатора .
Уравнение (2) даёт всю информацию ,
необходимую для создания классификатора.
Основной характеристикой, представляющей
классификатор , является дискриминантная
функция
,
которая определяется как
.
Возникает вопрос
, что в действительности делает
?
Чтобы ответить на этот вопрос , рассмотрим
несколько испытательных образов(т.е.
образов точная классификация которых
неизвестна), которые обозначим как
.
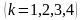Вычислим теперь значение для каждого из испытательных образов
Рассмотрение
последнего выражения приводит к выводу,
что когда образ
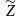лежит справа от решающей границы, то
>0 и наоборот , когда образ
лежит слева от решающей границы, то
<0. Все точки лежащие справа от границы
ближе к
,
а точки , лежащие слева от границы ближе
к
. Таким образом , благодаря дискриминантной
функции
получим следующее простое решающее
правило :
если
>0 , то
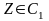
если
>0 , то
Описанный выше классификатор ,называемый элементом линейной пороговой логики, реализуется как показано на рис. 23.3.
Рис. 23.3
Получив дискриминантную функцию , говорят, что классификатор обучен, т.е. способен классифицировать образы с помощью соответствующего решающего правила. Элемент пороговой логики является классификатором , работающим по критерию минимума расстояния , так как решающее правило может быть сформулировано также следующим образом:
если
ближе к
, то
и если ближе к , то
Рассмотрим элемент
линейной пороговой логики, на который
воздействуют
образы , где
. В этом случае
. Соответствующая дискриминантная
функция записывается как
где
-
веса или параметры классификатора , а
- порог. Веса
и
получаются из обучающего множества.
Границей в этом случае является
гиперплоскость, определяемая как
Рис. 23.4