22. Виды разделяющих функций. Классификатор по минимальному расстоянию
А. Линейные разделяющие функции.
В этом случае в
качестве
используется линейная комбинация
измеренных признаков
Решающая
граница между областями
и
в пространстве признаков
имеет вид
(22.1)
где
Уравнение (22.1) представляет собой уравнение гиперплоскости в пространстве признаков .
Общая схема вычислителя линейной разделяющей функции представлена на рис. 22.1.
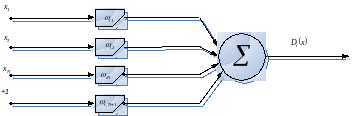Рис.
22.1
Если
,то
согласно (22.1)
и в качестве классификатора , использующего
линейную разделяющую функцию , можно
применить пороговый логический элемент.
Рис.
22.2
Из этого рисунка
получим , что если выходной сигнал =+1 ,
т.е. при , то
;
если выходной сигнал=-1, т.е.
, то
.
Когда число классов
образов больше двух, т.е.
можно применить параллельное соединение
нескольких пороговых логических
элементов. При этом комбинации выходных
сигналов
пороговых логических элементов достаточны
для различения
классов при
.
B.Классификатор по минимальному расстоянию.
Важный класс
составляют линейные классификаторы ,
в которых в качестве критерия классификации
используется расстояние между входным
образом и множеством опорных векторов
или эталонных точек в пространстве
признаков. Предположим , что задано
опорных векторов
, где
соответствует классу образов
.
При классификации по минимальному
расстоянию относительно
входной сигнал
предполагается принадлежащим
, т.е.
, если
минимально , где
есть расстояние между
и
.
Расстояние можно определить ,например, следующим образом
, (22.2)
где
индекс
определяет операцию транспонирования
вектора.
Из последнего соотношения следует, что
Так как
не зависит от
, то соответствующая разделяющая функция
для классификатора по минимальному
расстоянию имеет вид
Как видно из этого соотношения, классификатор по минимальному расстоянию является линейной функцией. В свою очередь, свойства классификатора по минимальному расстоянию конечно зависят от того, как выбраны опорные векторы.
С. Кусочно-линейная разделяющая функция.
Изложенная выше
идея может быть распространена на
классификацию по минимальным расстояниям
до
множеств опорных векторов. Пусть
обозначают
множеств опорных векторов, относящихся
соответственно к классам
и пусть опорные векторы в
обозначены через
,
т.е.
где
-число опорных векторов множества
.Определим
расстояние между вектором входных
признаков и
следующим образом.
То есть расстояние между и равно наименьшему из расстояний между и каждым вектором в .Такой классификатор будет относить входной сигнал к классу образов, которому соответствует ближайшее множество векторов.
Если расстояние между и определить согласно (22.1) разделяющая функция в данном случае имеет вид
Пусть
,
Тогда
Следует
отметить ,что
является линейной комбинацией признаков
.Поэтому указанный классификатор часто
называют кусочно-линейным классификатором.
D. Полиномиальная разделяющая функция.
Полиномиальная
функция
-ой
степени может быть представлена в виде
,
где
является формой
при
Решающая граница
между двумя классами также имеет форму
полинома
-ой
степени. В частности , если
,
решающая функция называется квадратичной.
В этом случае
при
Разделяющая функция будет иметь вид
,
где
В общем случае границей для квадратичных разделяющих функций является гиперболоид. В частных случаях это будут гиперсфера, гиперэллипсоид и гиперэллипсоидальный цилиндр. Общая схема вычислителя квадратичного разделения показана на рис. 22.3
Рис. 22.3