10. Функции спектральной плотности и определения спектров с помощью корреляционных функций

Функции спектральной плотности можно определить:

1. с помощью ковариационной функции

2. с помощью фильтрации, возведения в квадрат и усреднения.

Пусть существуют ковариационные и взаимные ковариационные функции , и , задаваемые формулами.

(10.1)

Предположим далее, что конечны интегралы от их абсолютных величин:

(10.2)

На практике это условие всегда выполняется и для реализаций конечной длины. Тогда:

(10.3)

где , называются функциями спектральной плотности мощности процессов и , а называется взаимной спектральной плотностью мощности процессов и .

Обратные преобразования дают:

(10.4)

Соотношения называют формулами Винера – Хинчина, которые в начале 30-х годов независимо установили связь между ковариационными функциями и спектральными плотностями через преобразование Фурье.

Из свойств симметрии ковариационных функций следует, что

(10.5)

Следовательно, спектральные плотности и - действительные чётные функции от f, а взаимная спектральная плотность - комплексная функция от f.

По определению:

(10.6)

То есть .

Выполнив в первом интеграле замену переменных, положив , . Тогда:

Так как , то тогда:

Спектральное соотношение можно преобразовать к виду

(10.7)

Обратные преобразования имеют вид

(10.8)

Односторонние спектральные плотности , , где f изменяется только в пределах интервала определяется формулами

, (10.9)

а вне указанной области значений f имеем

Односторонние спектральные плотности , связаны с ковариационными функциями , соотношениями

(10.10)

Обратные преобразования имеют вид:

(10.11)

При получим

(10.12)

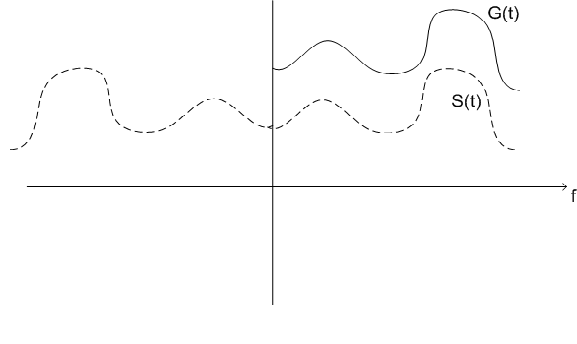
Рис. 10.1

В свою очередь односторонняя взаимная спектральная плотность определяется как:

(10.13)

где - называется спектральной плотностью (коспектром), а - квадратурной спектральной плотностью (квадратурный спектр).

Взаимная ковариационная функция определяется как:

(10.14)

При

. (10.15)

Одностороннюю взаимную спектральную плотность можно представить в комплексной полярной форме

(10.16)

где

Знаки членов и могут быть как положительными, так и отрицательными и их сочетание определяет квадрант, в котором расположен фазовый угол.

11. Определение спектров с помощью фильтрации

Другой способ вычисления спектральной плотности подразумевает применение аналоговых устройств и включает операции, схематически представленные на рис. 11.1:

Рис. 11.1. Вычисление спектральной плотности

1. Частотную фильтрацию сигнала x(t) с помощью узкополосного фильтра с полосой пропускания Δf и центральной частотой f₀. В результате этой операции получается величина x(f₀, Δf, t).

2. Возведение в квадрат мгновенного значения отфильтрованного сигнала

3. Усреднение квадрата мгновенного значения по реализации длины Т; в результате этой операции получается оценка среднего квадрата отфильтрованного сигнала

4. Деление на ширину полосы пропускания фильтра Δf, в результате чего получается оценка скорости изменения среднего квадрата в зависимости от центральной частоты f_0.

Следовательно, оценка СПМ имеет вид:

(11.1)

Для вычисления взаимной спектральной плотности аналоговыми методами применяется прямое обобщение описанной процедуры на случай двух сигналов x(t), y(t), которая включает следующие операции:

1. раздельная частотная фильтрация обоих сигналов с помощью узкополосных фильтров, имеющие одинаковые полосы пропускания Δf и одну и ту же центральную частоту f₀: в результате получаются x(f₀, Δf, t) и y(f₀, Δf, t)

2. перемножение мгновенных значений двух отфильтрованных сигналов при отсутствии сдвига фазы между ними с целью получения синфазных членов, необходимых для вычисления коспектра.

3. перемножение мгновенных значений двух отфильтрованных сигналов, причём y(f₀, Δf, t) сдвигается по фазе на 90^o по отношению к x(f₀, Δf, t) с целью получения смещённых по фазе членов, что необходимо для вычисления квадратурного спектра.

4. усреднение каждого из этих произведений по реализации длиной Т с целью построения оценок средних произведений оценок синфазных и смещённых по фазе членов.

5. деление каждого из средних произведений на ширину полосы пропускания Δf для получения оценок и .

Тогда оценка взаимной спектральной плотности имеет вид:

, (11.2)

где

Здесь - сдвинутый по фазе отфильтрованный сигнал y(f₀, Δf, t).

В случае конечного преобразования Фурье

Величина

(11.3)

действует как фильтр, выделяющий значение среднего квадрата в узкой полосе частот, окружающей центральную частоту f.

Чтобы доказать это, определим для любой реализации процесса величину

(11.4)

Тогда средний квадрат конкретной реализации можно определить как:

(11.5)

Согласно теореме Парсеваля . (11.6)