3.1.4. Метод двух узлов при расчете нелинейных электрических цепей

Если нелинейная разветвленная электрическая цепь имеет два узла, то за аргумент в исходной системе нелинейных алгебраических уравнений можно принять напряжение между двумя узлами. Это позволит решить графически одно нелинейное уравнение.

Порядок расчета рассмотрим на примере.

Пример.

Дано: на рис. 3.16 представлена нелинейная электрическая цепь в виде схемы замещения; на рис. 3.17 - в первом квадранте ВАХ нелинейных резистивных элементов; Е₁, Е₂ и Е₃.

Найти: все токи I_1, I₂, I₃, I₄ и падения напряжения на нелинейных элементах U₁, U₂, U₃, U₄.

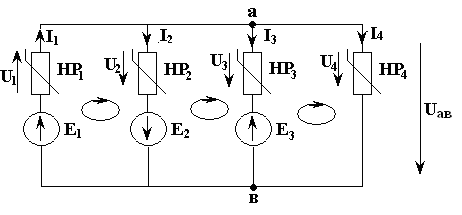
Рис. 3.16

Решение.

1) Составим систему уравнений по законам Кирхгофа:

(3.12)

2) За функции примем токи в ветвях, а за аргумент напряжение между двумя узлами U_aв. С учетом сказанного, исходную систему уравнений (3.12) можно представить в следующем виде. Для этого перепишем первое уравнение системы в виде функций от напряжения U_aв:

. (3.13)

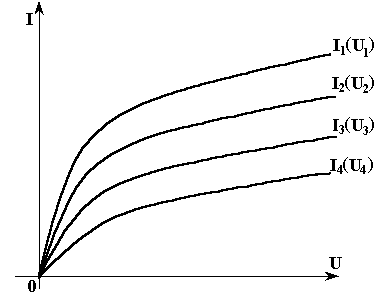
Рис. 3.17

Ампер-вольтные характеристики уравнения (3.13) будем строить по формулам, полученным с помощью второго закона Кирхгофа. Для этого составим уравнения для четырех контуров (см. рис. 3.16 и 3.18), образованных вектором U_aв и первой ветвью,

; (3.14)

вектором U_aв и второй ветвью,

; (3.15)

вектором U_aв и третьей ветвью,

; (3.16)

вектором U_aв и четвертой ветвью,

. (3.17)

Из уравнений (3.14) – (3.17) получим зависимости для требуемых вах:

(3.18)

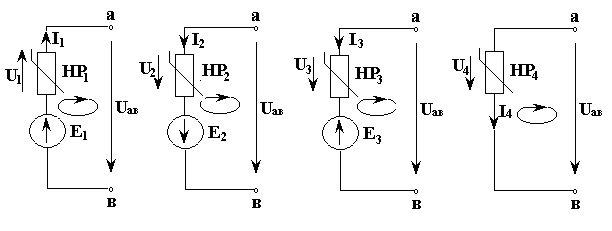
Рис. 3.18

Используя графики рис. 3.17 и заданные ЭДС, построим ВАХ по (3.18) , которые представлены на рис. 3.19 как , , и соответственно.

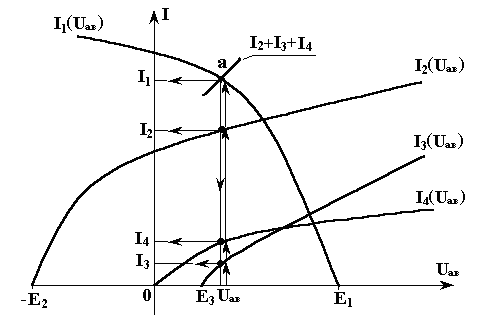
Рис. 3.19

3) Решим уравнение (3.13) графически, см. рис. 2.1. На рис. 3.19 построим график правой части уравнения (3.13): . Точка а пересечения этого суммарного графика с графиком левой части уравнения (3.13) и будет рабочей точкой, из которой опускаем перпендикуляр на ось абсцисс и находим значение напряжения , затем по следующему алгоритму определим токи:

U_ав I₁(U_ав) I₁;

I₂(U_ав) I₂;

I₃(U_ав) I₃;

I ₄(U_ав) I₄.

По полученным значениям токов и по ВАХ рис. 3.17 находим падения напряжения на нелинейных резисторах:

I _k U_k (I_k) U_k,

где к = 1,2,3,4.

Отметим, что рабочая точка а может лежать в любом квадрате.

Так как ВАХ нелинейного резистивного элемента симметрична относительно начала координат (рис. 3.17), то при нахождении рабочей точки а можно достроить недостающие части ВАХ с учетом указанной симметрии. Значения токов и напряжения между двумя узлами снимаются с соответствующих осей со своими знаками.

3.1.5. Расчет нелинейной электрической цепи с одним нелинейным элементом

Если в нелинейной электрической цепи будет только один нелинейный элемент, то при расчете можно использовать метод эквивалентного генератора. Постановка задачи аналогична предыдущей.

Порядок расчета.

1) Нелинейный элемент принимаем за нагрузку, а всю оставшуюся цепь за активный двухполюсник (или за эквивалентный генератор), рис. 3.20. Определим параметры эквивалентного генератора Е_г и R_г.

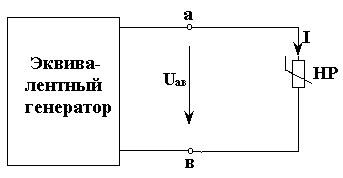
Рис. 3.20

2) Проделаем опыт холостого хода. Удалим нелинейный элемент и опытным или расчетным путем определим напряжение U_ab,о на разомкнутых зажимах оставшейся электрической схемы, рис. 3.21а, отсюда находим ЭДС генератора .

а) б)

Рис. 3.21

3) Определим сопротивление эквивалентного генератора R_г, которое будет равно внутреннему сопротивлению оставшейся схемы R_ab относительно разомкнутых зажимов, рис. 3.21б.

4) Нарисуем расчетную схему, в которой к эквивалентному генератору подключим удаленный ранее нелинейный элемент, рис. 3.22.

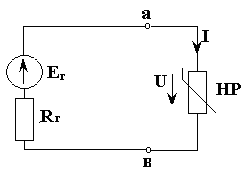
Рис. 3.22

5) Составим по второму закону Кирхгофа уравнение

U(I)+R_гI=E_г,

которое в дальнейшем решим графически, как в р. 2.1 и 3.1.1.