Решение.

Для схемы рис. 3.6а запишем уравнение по второму закону Кирхгофа

,

откуда получим результирующую ВАХ

,

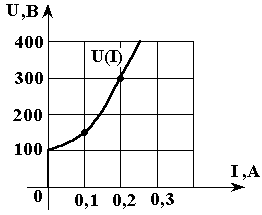
Рис. 3.7

которая показана на рис. 3.7.

3.1.2. Параллельное соединение нелинейных элементов

Так же как в предыдущем разделе, рассмотрим два метода решения уравнения.

Пример 1.

Задана электрическая схема, рис. 3.8, ВАХ нелинейных элементов и входной ток . Требуется найти оставшиеся токи в ветвях и входное напряжение.

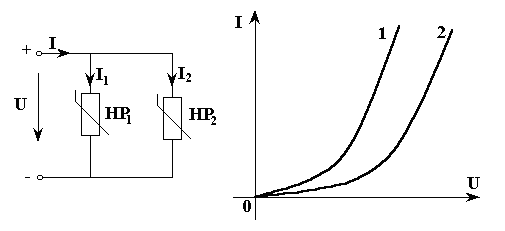
а) б)

Рис. 3.8

Решение.

Для заданной схемы запишем уравнение по первому закону Кирхгофа

. (3.5)

Примем за аргумент входное напряжение и перепишем уравнение (3.5) в виде

. (3.6)

а) Метод преобразования.

Построим результирующую ВАХ по (3.6) (даем значения напряжению и складываем токи), рис. 3.9.

Рис. 3.9

По заданному значению входного тока определяем требуемые по условию величины токов и входного напряжения:

.

Найденные значения токов должны удовлетворять уравнению (3.5)

.

б) Метод пересечения.

Подставим значения тока в уравнение (3.6) и перепишем его в виде

. (3.7)

Найдем точку пересечения графиков левой и правой частей уравнения (3.7), рис. 3.10. Определим входное напряжение , по которому найдем токи:

.

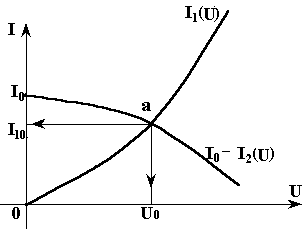
Рис. 3.10

Пример 2.

Для электрической схемы, заданной ВАХ нелинейного резистора, нарисовать эквивалентную ВАХ, рис. 3.11.

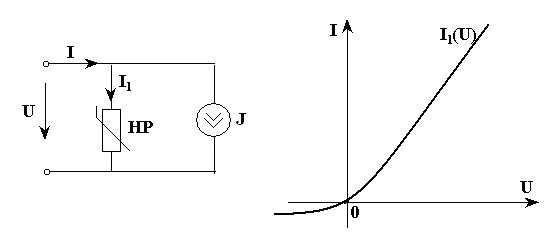
Рис. 3.11

.

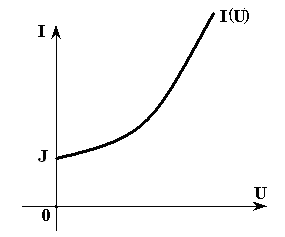
Рис. 3.12

Решение.

По первому закону Кирхгофа получим эквивалентную ампер-вольтную характеристику , которая представлена на рис. 3.12.

3.1.3. Смешанное соединение элементов

В предыдущих разделах графически решалось одно уравнение. В этом разделе будем решать графически систему нелинейных уравнений.

Пример 1.

Заданы нелинейная электрическая схема, ВАХ нелинейных элементов и входное напряжение U=U₀. Требуется найти все токи в ветвях и падение напряжения на элементах, рис. 3.13.

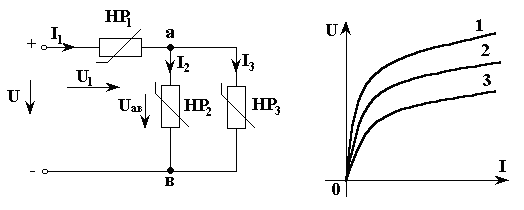
а) б)

Рис. 3.13

Решение.

1) Составим систему уравнений по законам Кирхгофа:

I₁=I₂+I₃,

U₁+U_ab=U,

U₂=U₃=U_ab.

В зависимости от вида соединения элементов (см. разделы 3.1.1. и 3.1.2.), выберем аргументы и перепишем систему (3.10) в следующем виде:

(3.11)

Первое уравнение системы (3.11) соответствует замене параллельного участка схемы рис. 3.13а, а второе определяет эквивалентную ВАХ всей схемы при последовательном соединении элементов.

Указанные эквивалентные преобразования исходной схемы рис. 3.13а приведены на рис. 3.14.

2) Найдем ампер-вольтную характеристику I₁(U_ab) эквивалентного нелинейного сопротивления HP₂₃, рис. 3.14а , по первому уравнению системы (3.11). Здесь и далее построения будем делать на рис. 3.15.

3) Схему рис. 3.14а преобразуем в схему рис. 3.14б, для этого найдем результирующую вольт-амперную характеристику U(I₁) по второму уравнению системы (3.11). У полученной в п. 2 зависимости I₁(U_ab) аргумент и функцию поменяем местами, тогда, давая значения току I_1, сложим напряжения U₁(I₁) и U_ab(I₁). Полученная таким образом ВАХ U(I₁) соответствует схеме рис. 3.14б.

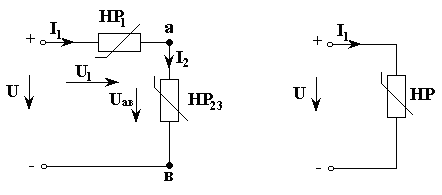
а) б)

Рис. 3.14

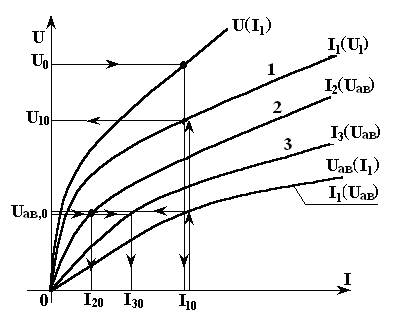
Рис. 3.15

3) На рис. 3.15 реализован следующий алгоритм нахождения требуемых значений токов и падений напряжений:

U₀ U(I₁) I₁₀ U_ав(I₁) U_ав,0 I₂(U_ав) I₂₀;

U ₁(I₁) U₁₀; I₃(U_ав) I₃₀.

Пример 2.

Используя данные и построения предыдущего примера, необходимо написать алгоритм определения остальных токов и напряжений при заданных: a) I₁=I₁₀ и б) I₃=I₃₀.

Решение.

a) Напишем алгоритм при условии п.а. Для этого используем схемы рис. 3.14а и 3.13а, а также соответствующие построения рис. 3.15:

I ₁₀ U_ав(I₁) U_ав,0 I₂(U_ав) I₂₀;

U₁(I₁) U₁₀; I₃(U_ав) I₃₀.

б) Для условия п.б алгоритм решения примет следующий вид:

I ₃₀ U₃(I₃) U₃₀ = U_ав,0 = U₂₀ I₂(U₂₀) I₂₀

I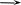 ₁₀ = I₂₀+ I₃₀ U₁(I₁) U₁₀.

Из приведенного алгоритма видно, что при таком условии задачи не требуется преобразовывать исходную схему в схемы рис. 3.14, а достаточно использовать заданные ВАХ элементов, рис. 3.13б.