2.3. Моделирование

Моделирование условно можно разбить на три типа – это цифровое, аналоговое и физическое.

Цифровое моделирование осуществляется с помощью цифровых вычислительных машин, аналоговое – с помощью аналоговых вычислительных машин и физическое - с помощью модельных (лабораторных) физических установок и устройств, являющихся аналогами реальных. Каждый из типов может быть разделен еще на несколько, кроме того, при решении реальных задач они могут сочетаться друг с другом.

Рассмотрим суть моделирования на примере цифрового.

Суть сводится к составлению системы уравнений по законам Кирхгофа и к решению их на компьютере, т.е. составляется математическая модель, которая далее реализуется на компьютере.

В настоящее время разработаны и получили распространение программы, например, Electronics Workbench, которая реализует блочный принцип моделирования, т.е. общая модель какой-либо электрической цепи получается из «сшивания» отдельных блоков (моделей) элементов этой цепи, которая затем исследуется.

3. Расчет нелинейных электрических цепей

постоянного тока

В данной главе рассмотрим только графические методы расчета.

3.1. Графические методы расчета

Применяются для расчета простых электрических цепей. Рассмотрим примеры расчета при последовательном, параллельном и смешанном соединениях нелинейных элементов, а также метод двух узлов при расчете разветвленных нелинейных электрических цепей.

3.1.1. Последовательное соединение нелинейных элементов

Рассмотрим два метода расчета – метод преобразования и метод пересечения (см. раздел 2.1).

Пример 1.

Задана электрическая цепь, рис. 3.1, с ВАХ нелинейных элементов, рис. 3.2. Требуется определить токи и падения напряжения на элементах при заданном входном напряжении .

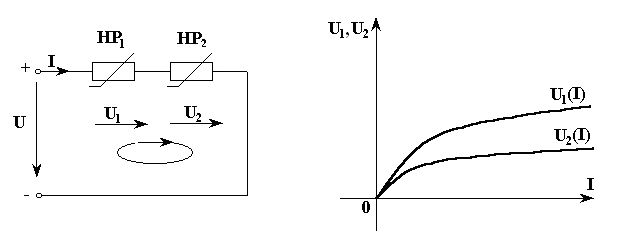
Рис. 3.1 Рис. 3.2

Порядок расчета.

1) Составим уравнение по второму закону Кирхгофа

, (3.1)

которое будет справедливо только в одной рабочей точке при заданном входном напряжении, например, при .

2) Решим уравнение (3.1) двумя методами.

а) Метод преобразования характеристик. Найдем результирующую вольт-амперную характеристику всей цепи. За аргумент примем ток, т.к. он будет одним и тем же при последовательном соединении элементов. Тогда уравнение (3.1) можно переписать в виде

. (3.2)

Используя (3.2) и заданные вольт-амперные характеристики рис. 3.2, построим результирующую вольтамперную характеристику , рис. 3.3.

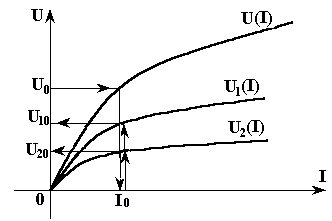
Рис. 3.3

Сделанное преобразование соответствует переходу от исходной схемы рис. 3.1 к схеме рис. 3.4.

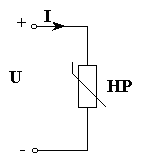
Рис. 3.4

На рис. 3.3 стрелками показан следующий алгоритм решения:

(3.3)

.

б) Метод пересечения характеристик.

В уравнение (3.1) подставим значение входного напряжения и перепишем уравнение в виде

. (3.4)

Построим на одном рисунке графики левой и правой частей уравнения (3.4), рис. 3.5. В точке пересечения графиков будет выполняться уравнение (3.4). Из графиков находим и , затем из уравнения (3.1) определим .

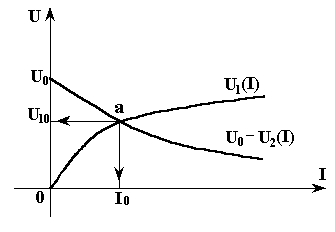
Рис. 3.5

Пример 2.

Для схемы рис. 3.6а и заданных ВАХ рис. 3.6б, В построить результирующую ВАХ.

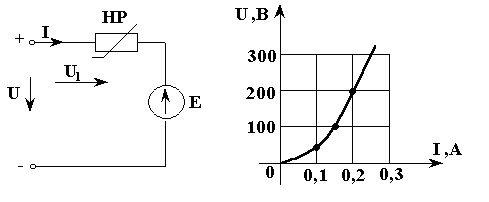
а) б)

Рис. 3.6