1.3. Параметры нелинейных элементов

При расчете нелинейных электрических цепей вводят понятия статических и дифференциальных параметров.

На основе вольт-амперной характеристики получают активные сопротивления: статическое r_С и дифференциальное r_d активные сопротивления, используя вебер-амперную характеристику, определяют индуктивность статическую L_C и дифференциальную L_d, по кулон-вольтной характеристике находят емкость статическую С_С и дифференциальную С_d.

Рассмотрим определение указанных параметров на примере нелинейного резистивного элемента, для которого задана ВАХ с рабочей точкой а (например, точка а соответствует номинальному режиму работы НР), рис. 1.7.

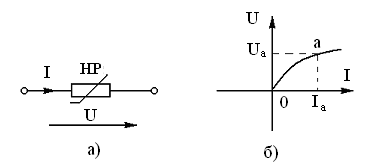
Рис. 1.7

Проведем прямую из начала координат через рабочую точку а, рис.1.8. Запишем уравнение прямой

, (1.7)

где - статическое сопротивление. Статическое сопротивление можно определить через тангенс угла α:

, (1.8)

здесь - масштаб сопротивления определен через масштабы напряжения и тока .

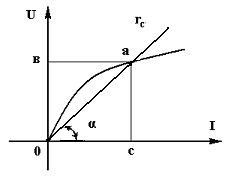
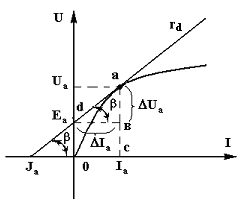
Рис. 1.8 Рис. 1.9

Проведем касательную к ВАХ в точке а и запишем ее уравнение, рис.1.9,

, (1.9)

где - дифференциальное сопротивление в точке а.

Отметим, что если ВАХ будет линейной, то дифференциальное и статическое сопротивления будут совпадать. При определенных условиях на линейных участках ВАХ они могут также совпадать. Если на теоретической вольт-амперной характеристике имеются «падающие» участки, то для этих участков дифференциальное сопротивление будет отрицательным, т.е. этот участок ВАХ будет физически нереализуем.

Рассмотрим примеры использования статического и дифференциального сопротивлений. Пусть указанные сопротивления определены по вольт-амперным характеристикам, требуется нарисовать линейные схемы замещения нелинейных резистивных элементов для двух режимов работы:

1. входное напряжение U может изменяться от нуля до , т.е. ;

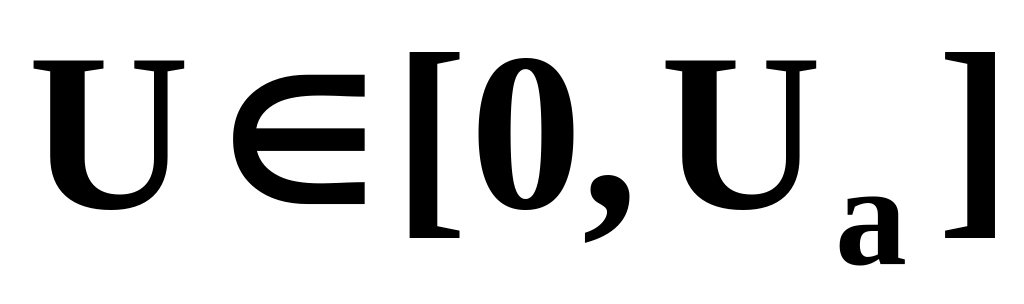2. входное напряжение отклоняется незначительно от номинального .

Для первого режима схема замещения будет получена путем реализации уравнения (1.7), рис.1.10. По уравнению (1.9) нарисуем схему замещения для второго режима работы, рис.1.11.

Отметим, что вопросы точности при замене (аппроксимации) здесь не рассматривались.

Аналогично определяются статические и дифференциальные параметры индуктивного и емкостного элементов:

, ,

(1.10)

, .

Кроме приведенных выше статических и дифференциальных параметров, при расчетах нелинейных электрических цепей переменного тока используют усредненные параметры нелинейных элементов (r, L и С), или их сопротивления, полученные для основной частоты и для номинального режима работы цепи. Например, по действующим значениям периодических несинусоидальных напряжений и токов имеем:

, , , (1.11)

или по их первым гармоникам.

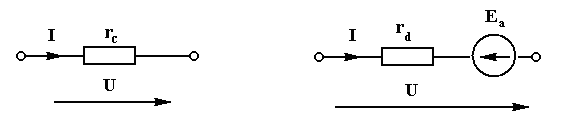
Рис. 1.10. Рис. 1.11.

При этом эквивалентные параметры находятся по формулам:

, , (1.12)

где - частота несинусоидального напряжения и тока (основная частота).

Ясно, что при изменении режима работы цепи (или частоты) приведенные выше параметры изменят свои значения.