4.1.3. Расчет постоянного магнита с воздушным зазором

На рис. 4.14 показан кольцевой постоянный магнит с воздушным зазором. Сердечник магнита выполнен из магнитотвердой стали, длина воздушного зазора l_в значительно меньше длины сердечника l_c . Сталь намагничена до насыщения. Заданы площадь сечения S_cm и длины участков l_cm и l_в магнитопровода, кривая размагничивания В(Н), рис. 4.15. Требуется найти магнитный поток в воздушном зазоре.

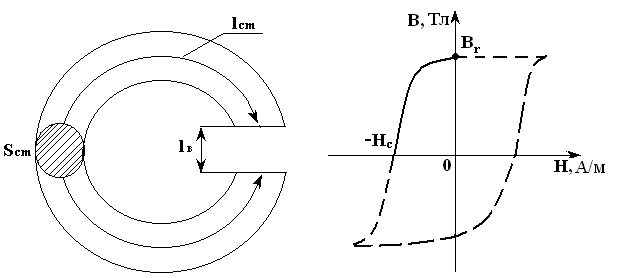
Рис. 4.14 Рис. 4.15

При отсутствии воздушного зазора по второму закону Кирхгофа для магнитной цепи имеем

Н_cml_cm=0.

Отсюда следует, что напряженность магнитного поля в стальном сердечнике будет равна нулю Н_cm=0, а индукция в сердечнике будет равна остаточной В_cm=В_r, согласно графика рис. 4.15.

Запишем уравнение по второму закону Кирхгофа для магнитной цепи с воздушным зазором, рис. 4.14,

Н_cml_cm +H_вl_в = 0, (4.12)

из которого найдем напряженность магнитного поля в сердечнике

. (4.13)

В формуле (4.13) сделаем следующие подстановки:

,

где µ₀= 4π10^-7 Гн/м; В_в = В_cm, т.к. в магнитопроводе один и тот же магнитный поток Ф и сечение воздушного зазора принимаем равным сечению сердечника

S_в=S_сm ( , ).

Тогда формула (4.13) примет вид

, (4.14)

где коэффициент размагничивания . (4.15)

На рис. 4.15 показаны направления векторов напряженности и индукции магнитного поля в магнитопроводе. При этом выполняются соотношения:

из формулы (4.14) следует, что

Н_cm<0, (4.16)

тогда

В_cm=B_в<В_r=µ₀J, (4.17)

т. к. В_cm=µ₀J+µ₀H_cm= В_r+µ₀·H_cm, где J-вектор намагниченности стали.

Отсюда следует, что рабочая точка с координатами Н_сm<0 и B_cm<B_r будет лежать на кривой размагничивания В(Н) (во втором квадранте), рис.4.15.

Решим графически систему уравнений, состоящую из линейного уравнения (4.14) и кривой размагничивания В(Н), представленной на рис. 4.15:

Н_cm= - N В_cm, (4.18)

В_cm(Н_cm). (4.19)

Находим коэффициент размагничивания по формуле (4.15), используя конструктивные размеры магнитопровода:

.

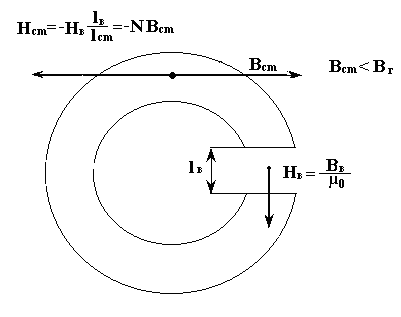
Рис. 4.16

Найденное значение N подставим в уравнение (4.18).

В одной системе координат нарисуем графики зависимостей (4.18) и (4.19). Точка пересечения графиков дает рабочую точку а, рис. 4.17. Находим ее координаты Н_ст и В_ст, затем, согласно постановки задачи, находим магнитный поток в воздушном зазоре Ф=В_вS_в= В_cmS_cm.

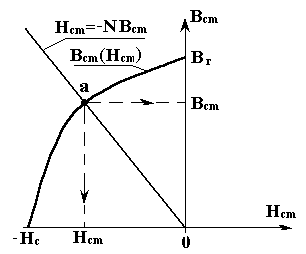
Рис. 4.17

5. Расчет нелинейных электрических цепей переменного тока

Рассмотрим примеры расчета нелинейных электрических цепей переменного тока, а также основные методы расчета (в той или иной степени рассмотрены в гл.2).

5.1. Графический метод расчета по мгновенным значениям

Применяется для расчета простых нелинейных электрических цепей, содержащих однородные элементы, например, только нелинейные резистивные элементы (НР), или нелинейные индуктивные элементы (НИ), или нелинейные емкостные элементы (НЕ), см. р. 2.1.

Пример 1.

На рис. 5.1 показана электрическая цепь в виде схемы замещения, ВАХ диода представлена на рис. 5.2,

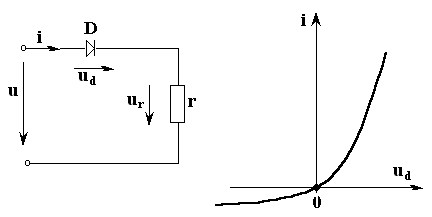
Рис. 5.1 Рис. 5.2

заданы значения сопротивления r и закон изменения входного напряжения u=U_msin(ωt).

Требуется построить графики изменения тока i, напряжений на элементах u_d и u_r от времени.

Решение сводится к графической реализации следующего алгоритма:

1. Найдем результирующую ВАХ всей цепи, составив уравнение по второму закону Кирхгофа, рис. 5.1,

, (5.1)

или

u(i)=u_d(i)+rI, (5.2)

где u_d(i) - ВАХ диода, рис.5.2.

1. Построим результирующую ВАХ (или i(U) – ампер-вольтную характеристику) по (5.2), рис. 5.3.

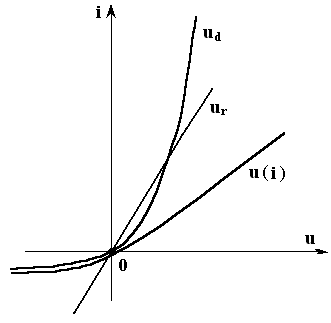
Рис. 5.3

3. Затем графически реализуем алгоритм, рис. 5.4:

t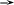 _n u[t_n] i(u) i[t_n] u_r[t_n]=r·i[t_n] (5.3)

u _d(i) u_d[t_n] ;

здесь t_n [0,T] дискретные значения времени на периоде .

На рис.5.4 масштабы по одноименным осям выбраны одинаковыми. Стрелками и цифрами от 1 до 6 показан один цикл построения. График изменения напряжения на резисторе u_r аналогичен закону изменения тока, поэтому график u_r не приводится.

Рис. 5.4

Пример 2

На рис. 5.5 показана схема с нелинейной индуктивностью, по которой протекает синусоидальный ток i=I_msin(ωt), на рис. 5.6 показана её вебер-амперная характеристика ψ(i). Требуется построить кривую изменения падения напряжения на нелинейной индуктивности u(t).

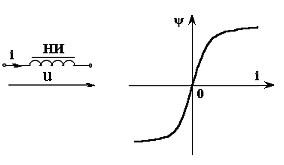
Рис. 5.5 Рис. 5.6

Запишем алгоритм решения в виде цепочки:

t_n i(t_n) ψ(i) ψ (t_n) u(t_n)= , (5.4)

где t_n [0,T], .

Реализуем алгоритм на графиках рис. 5.7.

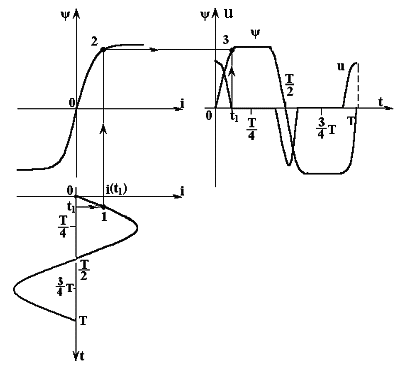
Рис. 5.7

Падение напряжения на нелинейной индуктивности u(t) получено путем дифференцирования кривой потокосцепления ψ(t).