4.1.2. Расчет разветвленной магнитной цепи

Рассмотрим два примера расчета разветвленной магнитной цепи, имеющей два узла.

Пример 1.

На рис.4.4а задана магнитная цепь. Конструктивные размеры l₁, l₂, l₃ и S₁, S₂, S₃, а также основная кривая намагничивания В(Н), рис.4.4б, значение потока Ф₃ = Ф_30. Требуется найти магнитодвижущую силу F, потоки Ф₁, Ф₂ и падение магнитного напряжения U_м,ab.

Таблица 4.1

В1	Н1	Ф=В1S1		Вв=В1	Н1	Н2		Н1l1	H2l2	2lвHв	F
Тл		Вб	Тл	Тл				А	А	А	А
В'	Н'	Ф'=В'S1		Вв'=В'	Н'	Н2'		Н' l1	H2' l2	2lвHв'	F'
В''	Н''	Ф''=В''S1		Вв''=В''	Н''	Н2''		Н'' l1	H2''l2	2lвHв''	F''
В''’	Н''’	Ф'''=В'''S1		Вв'''=В'''	Н'''	Н2'''		Н''' l1	H2''' l2	2lвHв'''	F'''
…

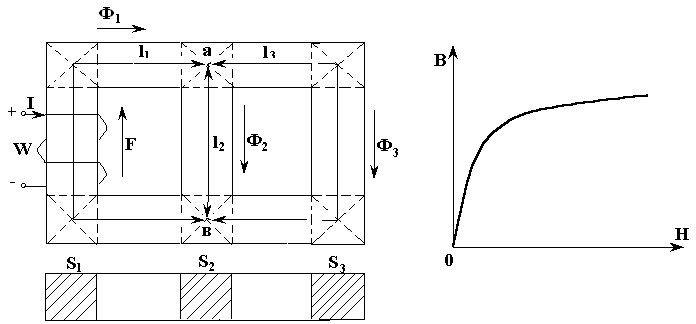
а) б)

Рис. 4.4

Решение.

1. Нарисуем схему замещения, рис. 4.5.

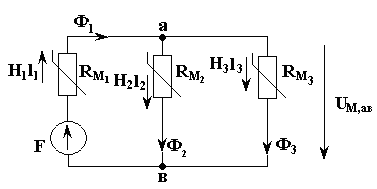
Рис. 4.5

2. По законам Кирхгофа для магнитных цепей запишем систему уравнений в удобном для решения виде:

(4.8)

3. Запишем алгоритм решения системы (4.8) в виде:

Ф ₃=Ф₃₀ B(H) H₃ U_м,aв = H₃l₃

B(H ) B₂ Ф₂=B₂S₂ Ф₁=Ф₂+Ф₃

B(H) H₁ F=H₁l₁+ U_м,aв.

Из приведенного алгоритма видно, что дополнительные графики строить не требуется. В алгоритме используется только график основной кривой намагничивания В(Н), рис. 4.4б.

Все требуемые значения Ф₁, Ф₂, U_м,aв и F будут найдены при реализации приведенного алгоритма.

Пример 2.

Задана магнитная цепь, рис. 4.6, основная кривая намагничивания В(Н) материала магнитопровода, рис. 4.7, конструктивные данные магнитопровода и катушек, табл. 4.2. Требуется найти магнитные потоки в сердечнике Ф₁, Ф₂ и Ф₃.

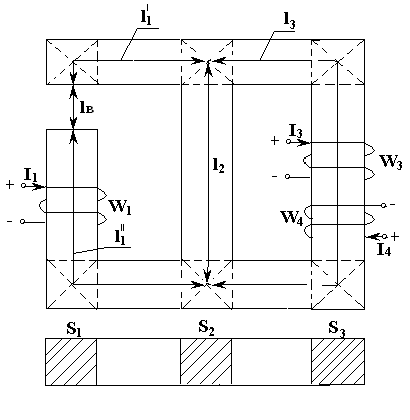
Рис. 4.6

Решение.

1. По исходной схеме рис. 4.6 нарисуем схему замещения, рис. 4.8. Выберем направления магнитных потоков, затем укажем падения напряжения на участках магнитопровода.

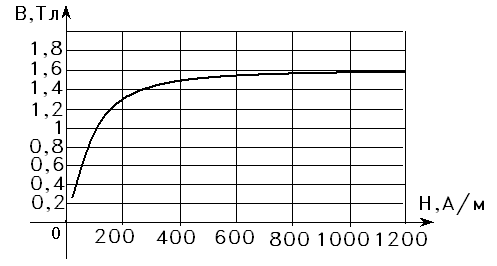
Рис. 4.7

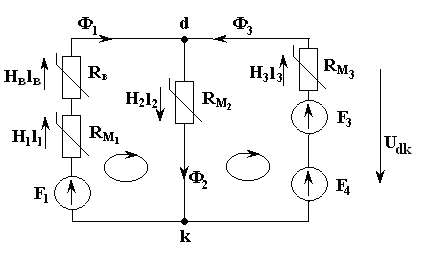
Рис. 4.8

2. Запишем систему уравнений по законам Кирхгофа:

(4.9)

3. Для графического решения системы нелинейных уравнений (4.9) воспользуемся методом двух узлов, см. р. 3.1.4. За функции выберем магнитные потоки Ф₁, Ф₂ и Ф₃, за аргумент примем напряжение между двумя узлами U_dk. Тогда первое уравнение системы (4.9) можно записать в следующем виде:

Ф₁(U_dk)+Ф₃(U_dk)=Ф₂(U_dk), (4.10)

где соответствующую зависимость потока от падения магнитного напряжения найдем на основе второго закона Кирхгофа при рассмотрении трех контуров, рис. 4.9.

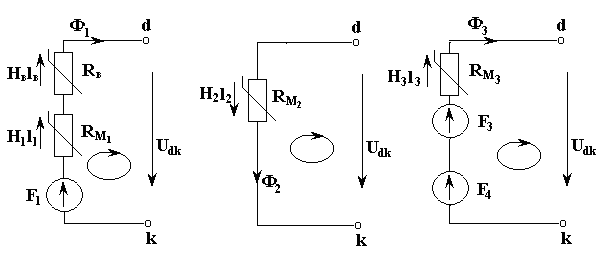
Рис. 4.9