Национальный исследовательский технологический
университет «МИСиС»
Кафедра физики
Лабораторная работа № 1
по дисциплине «Сопротивление материалов»
на тему: «Определение механических характеристик
материала по диаграмме растяжения»
Студент:
Группа:
Вариант №
Проверил: к.т.н., доц. Поляков Ю.А.
Москва, 2012
Цели работы:
1) получение диаграммы растяжения материала;
2) установление характерных особенностей диаграммы растяжения;
3) ознакомление с методикой определения характеристик прочности и пластичности исследуемого материала.
1. Основные понятия при центральном растяжении (сжатии) стержня
Центральное
растяжение (сжатие)
– вид нагружения, при котором в любом
поперечном сечении стержня возникает
только один внутренний силовой фактор
– нормальная
сила
,
которая всегда приложена к центру
тяжести поперечного сечения и направлена
вдоль оси симметрии стержня.
Рассмотрим
центральное растяжение стержня длиной
с прямоугольным поперечным сечением с
первоначальными размерами
(рис. 1). Приложим к свободным концам
стержня растягивающие силы
.
Тогда первоначальная длина стержня
увеличится на
,
а размеры поперечного сечения
соответственно уменьшатся на
и
.
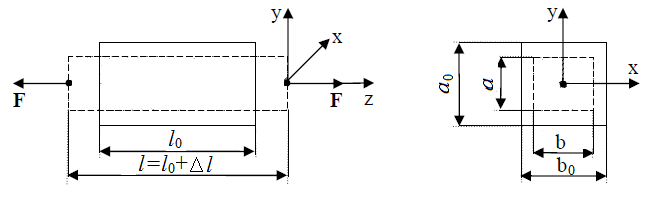
Рис. 1. Центральное растяжение стержня
Деформация – изменение формы и размеров тела под действием внешних сил.
– абсолютная
продольная деформация стержня
при – разность между длиной стержня
после и до деформации, измеряется в
метрах.
Относительная продольная деформация стержня (безразмерная величина) – отношение абсолютной продольной деформации стержня к его первоначальной длине:
получилась в
рассматриваемом случае положительной,
что соответствует увеличению длины
стержня при растяжении.пр
Относительная продольная деформация может быть выражена в процентах:
Относительная поперечная деформация стержня (безразмерная величина) – отношение изменения размера поперечного сечения к его первоначальному значению:
получились в
рассматриваемом случае отрицательными,
что соответствует уменьшению размеров
поперечного сечения стержня при
растяжении.
Для изотропных материалов относительные поперечные деформации равны между собой:
Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация прямо пропорциональна продольной:
Знак «минус» в этой формуле показывает, что продольная и поперечная деформации всегда противоположны по знаку.
– коэффициент
Пуассона
(безразмерный коэффициент пропорциональности)
– модуль отношения относительной
поперечной деформации к относительной
продольной деформации:
.
Для каждого конкретного материала – величина постоянная, характеризует упругие свойства материала и определяется экспериментально.
Для всех изотропных
материалов
Минимальное значение коэффициента
Пуассона для пробки (
),
а максимальное – для каучука (
).
Для большинства металлов и сплавов
Закон Гука при растяжении (сжатии). В пределах упругих деформаций (в пределах малых удлинений (укорочений)) относительная продольная деформация прямо пропорциональна нормальному напряжению:
.
– модуль
упругости первого рода (модуль Юнга)
– коэффициент пропорциональности,
характеризующий упругие свойства
материала, измеряется в мегапаскалях
(в МПа). Для каждого конкретного материала
модуль Юнга является постоянной величиной
и определяется экспериментально (для
сталей
).
Подставив закон
Гука в формулу, выражающую связь между
нормальной силой
и нормальным
напряжением
,
получаем:
где
–
площадь поперечного сечения стержня.
Подставив полученное
выражение для
в закон Гука, найдем зависимость
нормального напряжения от нормальной
силы для однородного (
)
стержня постоянного
поперечного сечения (
)
при
:
Поскольку
,
то абсолютная продольная деформация
однородного стержня постоянного
поперечного сечения при
:
.
Произведение
– жесткость
поперечного сечения
стержня
при растяжении (сжатии),
измеряется в ньютонах.
Величина
– жесткость
при растяжении (сжатии) стержня постоянного
сечения в целом.
Она численно равна силе, вызывающей
удлинение, равное единице длины. Чем
больше жесткость, тем меньше удлинение.