САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

МОРСКОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Гидроаэромеханики и морской акустики

Курсовая работа

Численное моделирование

в задачах гидромеханики

Исполнитель:

Балаш Дмитрий Алексеевич

Группа 1480

Проверил:

Бесядовский Александр Романович

Санкт-Петербург

2012 г.

Оглавление

Описание задачи			. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .								3
Методы решения			. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .								5
	Метод переменных направлений								. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .			5
	Метод Гаусса	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .									5
	Метод Гаусса-Зейделя					. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .						5
	Метод верхней релаксации						. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .					6
Программный код				. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .							8
Графики скорости сходимости решений										. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	17
Результаты вычислений					. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .						19
Список литературных источников								. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .				27

Описание задачи

Задача данного курсового проекта такова.

Существует пространство, в котором некий процесс описывается уравнением Лапласа:

Дискретный аналог (ДА) для этого уравнения для произвольного узла будет

а его коэффициенты равны

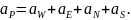
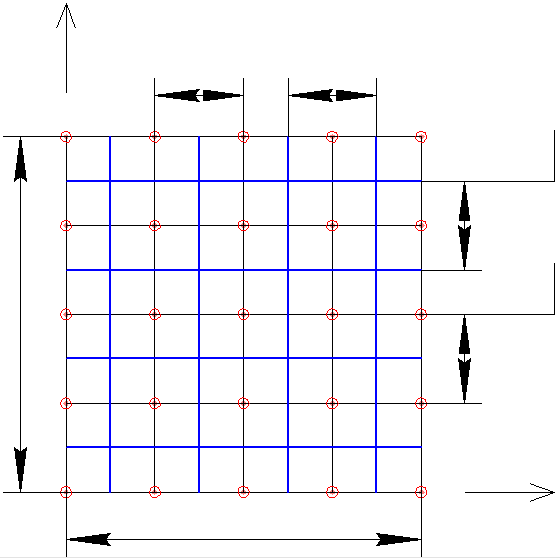
Рис. 1

Из всего пространства выделим произвольную расчётную область (рис. 1), где и – размеры расчётной области, и – размеры контрольного объёма и расстояние между узлами вдоль соответствующих осей (равномерная сетка).

На границах области выполняются следующие граничные условия (ГУ):

• верхняя граница: ;

• нижняя граница: ;

• левая граница: ;

• правая граница: .

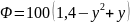Решение ДА выполнено четырьмя методами:

1. Переменных направлений

2. Гаусса

3. Гаусса-Зейделя

4. Верхней релаксации

Методы решения Метод переменных направлений

Этот метод также называют методом прогонки, алгоритмом Томаса или TDMA (Tri-Diagonal-Matrix Algorithm – трёхдиагональный матричный алгоритм). TDMA назван так из-за того, что ненулевые элементы матрицы коэффициентов группируются вдоль трёх диагоналей (главной и двух соседних).

Суть метода в том, что для начала прогонка применяется для всех линий, параллельных оси (линии перебираются снизу вверх и обратно), а затем повторяется для всех линий, параллельных оси (слева направо и обратно).

Этот метод обеспечивает быстрое «проникновение» информации о граничных условиях во внутреннюю часть расчётной области. В отличие от общих матричных методов TDMA требует машинных памяти и времени, пропорциональных , а не или .