Лабораторная работа № 1. Изучение источника постоянного тока

Цель работы: изучить функционирование фотоэлектрического приемника, снять вольт-амперную характеристику, определить характеристики фотоэлектрического преобразователя (ФЭП), оценить КПД элемента.

Общие сведения

В настоящее время применение известных и разработка новых экологи-

чески чистых источников электрической энергии приобретают особое значение в связи с неуклонно повышающимся уровнем загрязнения земной атмосферы двуокисью углерода сопровождающимся ростом влияния так называемого “парникового эффекта” и вызванным им потеплением климата нашей планеты. Среди наиболее перспективных источников такого рода важное место занимают полупроводниковые ФЭП солнечной энергии, в которых осуществляется прямой, одноступенчатый переход энергии. Достоинством этих устройств является безотходность технологии преобразования энергии и относительно простая конструкция.

К недостаткам ФЭП, прежде всего, следует отнести довольно низкие (в диапазоне 0,5 — 28 %) значения коэффициента полезного действия и высокую стоимость получаемой энергии. В настоящее время интенсивно развивается ряд направлений научных и технологических исследований, нацеленных на улучшение этих показателей ФЭП. Наиболее значимые результаты надеются получить от использования в качестве основы ФЭП аморфных полупроводниковых материалов и так называемых “тандемных” конструкций преобразователей солнечной энергии. Среди аморфных полупроводников наиболее перспективным для создания ФЭП считают гидрогенизированный аморфный кремний (a-Si:H) и сплавы на его основе. Для повышения эффективности преобразования солнечной энергии представляется привлекательным соединить в одном устройстве два (тандем) или более p-n переходов с тем, чтобы каждый из них работал с высокой эффективностью в ограниченном спектральном диапазоне.

Принцип работы ФЭП (рисунок 1)можно пояснить на примере преобразователей с p-n- переходом, которые широко применяются в современной солнечной и космической энергетике. Электронно-дырочный переход создаётся путём легирования пластинки монокристаллического полупроводникового материала с определённым типом проводимости (т.е. или p- или n- типа) примесью, обеспечивающей создание поверхностного слоя с проводимостью противоположного типа. Концентрация легирующей примеси в этом слое должна быть значительно выше, чем концентрация примеси в базовом (первоначальном монокристалле) материале, чтобы нейтрализовать имеющиеся там основные свободные носители заряда и создать проводимость противоположного знака. У границы n-и p- слоёв в результате перетечки зарядов образуются обеднённые зоны с нескомпенсированным объёмным положительным зарядом в n-слое и объёмным отрицательным зарядом в p-слое. Эти зоны в совокупности и образуют p-n-переход.

1- внешний электрод (-); 2 - защитное антибликовое покрытие; 3 - кремниевый n-слой; 4 - кремниевый p-слой; 5 - внутренний электрод (+)

Рисунок 1 – Принцип действия ФЭП

Возникший на переходе потенциальный барьер (контактная разность потенциалов) препятствует прохождению основных носителей заряда, т.е. электронов со стороны p-слоя, но беспрепятственно пропускают неосновные носители в противоположных направлениях. Это свойство p-n-переходов и определяет возможность получения фото-ЭДС при облучении ФЭП солнечным светом. Созданные светом в обоих слоях ФЭП неравновесные носители заряда (электронно-дырочные пары ) разделяются на p-n-переходе: неосновные носители (т.е.электроны) свободно проходят через переход , а основные (дырки) задерживаются. Таким образом, под действием солнечного излучения через p-n-переход в обоих направлениях будет протекать ток неравновесных неосновных носителей заряда- фотоэлектронов и фотодырок, что как раз и нужно для работы ФЭП. Если теперь замкнуть внешнюю цепь, то электроны из n-слоя, совершив работу на нагрузке, будут возвращаться в p-слой и там рекомбинировать(объединяться) с дырками, движущимися внутри ФЭП в противоположном направлении. Для сбора и отвода электронов во внешнюю цепь на поверхности полупроводниковой структуры ФЭП имеется контактная система. На передней освещённой поверхности преобразователя контакты выполняются в виде сетки или гребёнки, а на тыльной могут быть сплошными.

Генерацию электронно-дырочной пары вызывает излучение, чья энергия достаточна, чтобы разрушить связь электрона с ядром атома. Поэтому не все полупроводники являются чувствительными к солнечному излучению. По своему строению наиболее подходящими являются Si, GaAs, CdTe.

Характеристиками солнечного элемента являются ток короткого замыкания, напряжение холостого хода, максимальная мощность и коэффициент полезного действия (КПД). Напряжение холостого хода U_хх - напряжение между р- n- областями элемента, отсоединенного от внешней электрической цепи в основном определяется электрофизическими параметрами и степенью легирования материала, на основе которого изготовлен ФЭП. Ток короткого замыкания I_кз определяется при коротком замыкании между металлизированными контактами к p- и n- областям ФЭП. Величина I_кз зависит не только от электрофизических параметров прибора, но и от его площади, поэтому часто вместо I_кз используют другую характеристику – плотность тока короткого замыкания J_кз, которая равна отношению I_кз на площадь освещаемой поверхности элемента. Из-за резкой зависимости коэффициента поглощения полупроводника от энергии излучения измеряемые в эксперименте значения U_хх и I_кз будут в большой степени зависеть от спектрального состава оптического излучения. КПД показывает какая часть мощности падающего светового потока приведет к появлению электрической мощности на нагрузке.

На рисунке 2 показана типичная вольт-амперная характеристика ФЭП. Значения U_н и I_н – это напряжение и ток в нагрузочной цепи при режиме работы ФЭП, соответствующему максимальной выделяемой мощности на сопротивлении нагрузки.

Рисунок 2 – Вольт-амперная характеристика (ВАХ) ФЭП

Максимально выделяемая мощность равна площади прямоугольника, стороны которого определяются значениями U_н и I_н. Важным параметром ФЭП является коэффициент заполнения вольт-амперной характеристики ξ, определяемый отношением площади под световой вольт-амперной характеристикой элемента в первом квадранте системы координат на рисунке к площади прямоугольника со сторонами U_н и I_н. У современных солнечных элементов значения этого параметра находятся в пределах 0,75-0,8.

Основные необратимые потери энергии в ФЭП связаны с:

- отражением солнечного излучения от поверхности преобразователя,

- прохождением части излучения через ФЭП без поглощения в нём,

- рассеянием на тепловых колебаниях решётки избыточной энергии фотонов,

- рекомбинацией образовавшихся фото-пар на поверхностях и в объёме ФЭП,

- внутренним сопротивлением преобразователя и некоторыми другими

физическими процессами.

Для уменьшения всех видов потерь энергии в ФЭП разрабатываются и успешно применяется различные мероприятия. К их числу относятся:

- использование полупроводников с оптимальной для солнечного излучения шириной запрещённой зоны;

- направленное улучшение свойств полупроводниковой структуры путём её оптимального легирования и создания встроенных электрических полей;

- переход от гомогенных к гетерогенным и варизонным полупроводниковым структурам;

- оптимизация конструктивных параметров ФЭП (глубины залегания p-n-перехода, толщины базового слоя, частоты контактной сетки и др.);

- применение многофункциональных оптических покрытий, обеспечивающих просветление, терморегулирование и защиту ФЭП от космической радиации;

- разработка ФЭП, прозрачных в длинноволновой области солнечного спектра за краем основной полосы поглощения;

- создание каскадных ФЭП из специально подобранных по ширине запрещённой зоны полупроводников, позволяющих преобразовывать в каждом каскаде излучение, прошедшее через предыдущий каскад, и пр.

Описание лабораторной установки

Для снятия вольт-амперной характеристики ФЭП используется лабораторная установка, схема которой приведена на рисунке 3.

Рисунок 3 – Схема лабораторной установки

В качестве источника света используется лампа накаливания L. Питание лампы осуществляется от сети переменного тока. Сила тока через лампу регулируется реостатом R и измеряется миллиамперметром mA1. Свет от лампы падает на исследуемый образец ФЭП. Электрическая часть измерительной схемы включает источник питания измерительной цепи ИП, миллиамперметр mA2. В качестве источника питания используется источник постоянного тока. При замыкании ключа в положение 1снимается прямая ветвь вольт-амперной характеристики: (+) элемента соединяется с (+) ИП. При замыкании ключа в положение 2 меняется полярность подключения источника питания и снимается обратная ветвь вольт-амперной характеристики: (+) элемента соединяется с (-) ИП.

Мощность падающего светового потока можно определить, зная силу тока I₀, протекающего через лампу накаливания, и падение напряжения на ней U₀. Если считать источник света точечным и что поверхность исследуемого элемента располагается перпендикулярно световому потоку, тогда мощность падающего светового потока будет равна

, (1)

где ;

r – расстояние от нити накаливания до солнечного элемента;

S_ФЭП – площадь исследуемого элемента.

Коэффициент полезного действия (КПД) элемента можно оценить как отношение максимально выделяемой мощности P_max к падающей мощности

/ (2)

Программа работы

1 Установить исследуемый ФЭП на расстоянии 10 см от нити накаливания лампы. Накрыть лампу вместе с элементом колпаком. На источнике постоянного тока установить значение напряжения равное 0, ток – 0,30 А. Включить источник в розетку. Подключить лампу к сети переменного тока.

2 С помощью потенциометра R установить заданное преподавателем напряжение U₀ по шкале вольтметра V. Записать соответствующее значение силы тока I₀ по шкале миллиамперметра mA1. По полученным данным по формуле (1) рассчитать мощность падающего светового потока P₀. Данные занести в таблицу 1.

Таблица 1 – Результаты измерений

U0, В	I0, А	P0, Вт

3 Для снятия прямой ветви вольт-амперной характеристики замкнуть ключ. Изменяя напряжение на источнике постоянного тока ИП от 0 до 1.5 В с шагом 0,5 В и затем от 1,5 В с шагом 0,1 В, для каждого значения напряжения записать значения тока в измерительной цепи по шкале миллиамперметра mA2. Напряжение изменять до тех пор, пока сила тока не станет равна 0. Для каждой пары значений тока и напряжения рассчитать мощность солнечного элемента Р. Данные занести в таблицу 2.

Таблица 2 – Результаты измерений ВАХ

U, В
I, А
P, Вт

3 По данным таблицы 2 построить вольт-амперную характеристику ФЭП аналогично приведенной на рисунке 2. На построенную зависимость в первом квадранте нанести зависимость Р(I). По максимуму функции Р(I) графически определить значения I_н ,U_н и P_max.

4 По формуле (2) рассчитать КПД элемента при данных условиях. Занести в таблицу 3 основные характеристики исследуемого элемента. Ток короткого замыкания I_кз определяется при U=0, напряжение холостого хода U_хх при I=0.

Таблица 3 – Характеристики ФЭП

Uхх, В	Iкз , А	Uн, В	Iн, А	Рн, Вт	η

Контрольные вопросы

1 Поясните принцип действия ФЭП, постройте вольт-амперную характеристику ФЭП.

2 Основные характеристики ФЭП.

3 Как можно уменьшить потери энергии в ФЭП?

4 От чего зависит коэффициент полезного действия ФЭП?

Лабораторная работа № 2. Определение коэффициента трансформации и КПД трансформатора.

Цель работы: практически ознакомиться с работой трансформатора в различных режимах работы, определить коэффициент трансформации и КПД трансформатора при изменении нагрузки.

Общие сведения

С помощью трансформаторов повышается или понижается напряжение, изменяется число фаз, в некоторых случаях преобразуется частота переменного тока. Возможность передачи электрических сигналов от одной обмотки к другой посредством взаимоиндукции была открыта М. Фарадеем в 1831 г.: при изменении тока в одной из обмоток, намотанной на стальной магнитопровод, в другой обмотке индуцировались ЭДС. Однако первый практически работающий трансформатор создал известный изобретатель П. Н. Яблочков в содружестве с И. Ф. Усагиным в 1876 г.

Трансформатор – электомагнитное устройство, представляющее собой магнитопровод с нанесенными на него двумя или более обмотками, предназначенное для преобразования с помощью элетромагнитной индукции переменного тока одного напряжения в переменный ток другого (или других) напряжений. Обмотка трансформатора, к которой подводиться энергия преобразуемого переменного тока, называется первичной, а обмотка, от которой отводится энергия преобразованного переменного тока – вторичной. Эти обмотки называют основными. Существуют трансформаторы, у которых помимо первичной и вторичной обмоток, существует вспомогательные обмотки не связанные непосредственно с приемом или отдачей энергии преобразованного переменного тока.

Различают основные обмотки трансформатора высшего(ВН), низшего(НН) и среднего (СН) напряжений. Обмотка ВН имеет наибольшее номинальное напряжение по сравнению с другими основными обмотками трансформатора. Обмотка НН - наименьшее номинальное напряжение, а обмотка СН - номинальное напряжение, являющееся промежуточным между ВН и НН. Трансформатор, у которого первичной обмоткой является обмотка НН - называют повышающим. В конце линии передач, где начинается распределение энергии, устанавливают трансформаторы, снижающие напряжение линии до напряжений, необходимых потребителю. Первичной в таких трансформаторах служит обмотка ВН, а трансформаторы называются понижающими.

Различают однофазные (для цепей однофазного тока) и трехфазные (для трехфазных цепей) трансформаторы. Рабочий процесс однофазного трансформатора практически такой же, как и одной фазы трехфазного трансформатора. Рассмотрим работу однофазного двухобмоточного трансформатора (рисунок 1).

Рисунок 1- Принципиальная конструкция однофазного трансформатора

Предположим, что цепь вторичной обмотки трансформатора разомкнута и при действии источника напряжения ε = U₁ ток в первичной обмотке равен i₁. Намагничивающая (магнитодвижущая) сила i₁ ω₁ возбуждает в магнитопроводе магнитный поток Ф, который пронизывает витки и первичной и вторичной обмоток. Таким образом вторичная обмотка оказывается магнитно связанной с первичной при посредстве магнитных силовых линий. Так как ток i₁ - переменный, т. е. ток, меняющийся во времени по закону синуса, то и магнитное поле, им создаваемое, также будет меняться во времени по тому же закону. Например, когда ток в первичной обмотке проходит через наибольшее значение, то и магнитный поток, им создаваемый, также проходит через наибольшее значение; когда ток i₁ проходит через нуль, меняя свое направление, то и магнитный поток проходит через нуль, также меняя свое направление. В результате изменения тока обе обмотки пронизываются магнитным потоком, непрерывно меняющим свою величину и свое направление. Этот магнитный поток индуцирует в первичной обмотке ЭДС самоиндукции ε_L1 , а во вторичной обмотке - ЭДС взаимной индукции ε_M2 .

Часть магнитных линий охватывает отдельные витки, замыкается по воздуху и частично по магнитопроводу. Эти силовые линии в передаче электрической энергии от первичной обмотки ко второй совершенно не участвуют, они образуют так называемое поле рассеяния. Эта часть магнитного поля характеризуется потокосцеплением рассеяния первичной ψ_S1 и вторичной ψ_S2 обмоток, которые пропорциональны соответственно токам i₁ и i₂.

Для того чтобы увеличить магнитную связь между первичной и вторичной обмотками и одновременно уменьшить магнитное сопротивление для прохождения магнитного потока, обмотки технических трансформаторов располагают на совершенно замкнутых железных сердечниках.

На рисунке 2 схематически изображен однофазный трансформатор стержневого типа. У него первичные и вторичные катушки c₁ и с₂ расположены на железных стержнях а — а, соединенных с торцов железными же накладками b — b, называемыми ярмами. Таким образом два стержня а, а и два ярма b, b образуют замкнутое железное кольцо, в котором и проходит магнитный поток, сцепляющийся с первичной и вторичной обмотками. Это железное кольцо называется сердечником трансформатора.

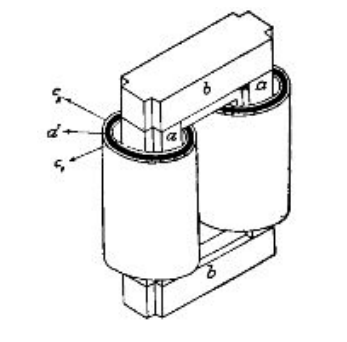
Рисунок 2- Однофазный трансформатор стержневого типа

На рисунке 3 схематически показан однофазный трансформатор броневого типа. У этого трансформатора первичные и вторичные обмотки с, состоящие каждая из ряда плоских катушек, расположены на сердечнике образуемом двумя стержнями двух железных колец а и b. Кольца а и b, окружая обмотки, покрывают их почти целиком как бы бронею, поэтому описываемый трансформатор и называется броневым. Магнитный поток, проходящий внутри обмоток с, разбивается на две равные части, замыкающиеся каждое в своем железном кольце.

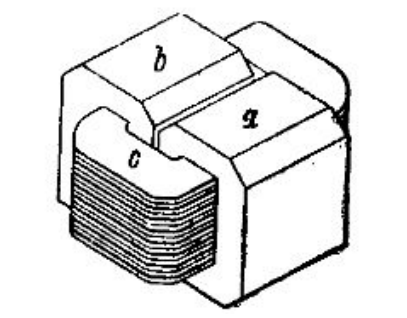
Рисунок3- Однофазный трансформатор броневого типа

Применением железных замкнутых магнитных цепей у трансформаторов добиваются значительного снижения потока рассеяния. У таких трансформаторов потоки, сцепляющиеся с первичной и вторичной обмотками, почти равны друг другу. На основании общего закона индукции мгновенные значения электродвижущих сил обмоток равны

; . (1)

Из (1) получаем следующее отношение:

,

т. е. индуктируемые в первичной и вторичной обмотках мгновенные значения электродвижущих сил относятся друг к другу так же, как числа витков катушек. Последнее заключение справедливо не только по отношению к мгновенным значениям электродвижущих сил, но и к их максимальным и действующим значениям.

Электродвижущая сила, индуктируемая в первичной, катушке, будучи электродвижущей силой самоиндукции, почти целиком уравновешивает приложенное к той же катушке напряжение. Если через E₁ и U₁ обозначить действующие значения электродвижущей силы первичной катушки и приложенного к ней напряжения, то Е₁ = U₁.

Электродвижущая сила, индуктируемая во вторичной катушке, равна в рассматриваемом случае напряжению на концах этой катушки. Если, аналогично предыдущему, через E₂ и U₂ обозначить действующие значения электродвижущей силы вторичной катушки и напряжения на ее концах, то Е₂ = U₂.

Следовательно, приложив к одной обмотке трансформатора некоторое напряжение, можно на концах другой обмотки получить любое напряжение, стоит только взять подходящее отношение между числами витков. В этом и заключается основное свойство трансформатора.

Отношение числа витков вторичной обмотки к числу витков первичной обмотки называется коэффициентом трансформации трансформатора k_Т

. (2)

После замыкания цепи вторичной обмотки под действием ЭДС взаимной индукции ε_M2 в приемнике с сопротивлением нагрузки R₂ возникнет ток i₂. С появлением тока во вторичной обмотке появится магнитодвижущая сила этой обмотки. Суммарная намагничивающая сила двух обмоток i₁ ω₁ и i₂ ω₂ создает основной магнитный поток Ф – магнитные линии замыкаются по магнитопроводу. Согласно правилу Ленца магнитодвижущая сила вторичной обмотки действует против магнитодвижущей силы первичной обмотки. В результате, в первичной обмотке нарушается компенсация ЭДС индукции и ЭДС источника питания, что приводит к увеличению тока в первичной обмотке, до тех пор, пока магнитный поток не достигнет практически прежнего значения. В этом режиме отношение токов первичной и вторичной обмотки равно обратному отношению числа витков обмоток

,

отношение напряжений в первом приближении также остаётся прежним. В результате, мощность, потребляемая от источника в цепи первичной обмотки практически полностью передаётся во вторичную.

Со стороны вторичной обмотки, содержащей ω₂ витков, т. е. для приемника с сопротивлением нагрузки R₂, трансформатор является источником энергии, а со стороны первичной обмотки, содержащей ω₁ витков, - приемником энергии от источника питания. Преобразование электрической энергии в трансформаторе сопровождается потерями энергии на нагрев сердечника и обмоток.

Различают следующие режимы работы трансформатора, имеющего номинальную полную мощность S_1НОМ = U_1НОМ I_1НОМ:

1) рабочий режим, при котором напряжение первичной обмотки близко к номинальному или равно ему, а ток I₁ меньше номинального значения I_1НОМ или равен ему и определяется нагрузкой трансформатора, т.е. током I₂ ;

2) режим холостого хода, т.е. режим ненагруженного трансформатора, при котором цепь вторичной обмотки разомкнута (I₂ = 0) или подключена к приемнику с очень большим сопротивлением нагрузки, например, к вольтметру;

3) режим короткого замыкания, при котором вторичная обмотка коротко замкнута (U₂ = 0) или подключена к приемнику с очень малым сопротивлением нагрузки, например, к амперметру.

Опыт холостого хода дает возможность определить коэффициент трансформации, ток холостого хода I₁₀, потери активной мощности P_С в стали. Потери активной мощности P_С в стали идут на перемагничивание магнитопровода, на компенсацию размагничивающего действия вихревых токов. Т.к. при номинальном напряжении на первичной обмотке магнитный поток практически постоянен, то независимо от того, нагружен трансформатор или нет, величина P_С для него является постоянной. Т.е. энергия, потребляемая из сети, расходуется только на потери в стали, поэтому мощность этих потерь можно измерить в режиме холостого хода.

Опыт короткого замыкания позволяет определить потери в обмотках трансформатора - потери в меди P_М, которые обусловлены активными сопротивлениями обмоток. Если вторичную обмотку замкнуть накоротко, а на первичную подать пониженное напряжение, при котором токи в обмотках не превышают номинальных значений, то энергия, потребляемая из сети, расходуется в основном на тепловые потери в проводах обмоток трансформатора. В этом опыте к первичной обмотке подводится пониженное напряжение, поэтому магнитный поток очень мал и потери в стали также малы.

Коэффициент полезного действия трансформатора (к.п.д.) – это отношение отдаваемой активной мощности к потребляемой:

,

где P₁ – мощность, потребляемая из сети;

P₂ – мощность, отдаваемая нагрузке.

Для практического определения к.п.д. при номинальной нагрузке необходимо измерить мощности в первичной и вторичной обмотках. При включении во вторичную обмотку активной нагрузки , т.к. cosφ = 1 (поток рассеяния невелик). Тогда P₂ можно определить по показаниям амперметра и вольтметра, включённых во вторичную цепь. Такой метод называется методом непосредственных измерений. Он прост, но имеет два существенных недостатка: малую точность и неэкономичность. К.п.д. промышленных трансформаторов очень высок - до 99%, поэтому P₁ и P₂ мало отличаются по величине. В этом случае незначительные ошибки в показаниях приборов приведут к большим ошибкам в значении к.п.д. Неэкономичность связана с большим расходом энергии во время испытаний. Поэтому этот способ годится для трансформаторов малой мощности с небольшим к.п.д. На практике к.п.д. трансформатора определяется косвенным методом, т.е. путём раздельного определения потерь. При этом к.п.д. трансформатора может быть представлен в следующем виде:

где ΔР - потери активной мощности в трансформаторе, которые складываются из потерь в стали P_С и из потерь в меди P_М.

С ростом отдаваемой мощности η увеличивается, т.к. в энергетическом балансе уменьшается удельное значение потерь в стали, имеющих приблизительно постоянное значение. К.п.д. будет максимальным при такой нагрузке, при которой потери в меди трансформатора будут равны потерям в стали.

Описание лабораторной установки

Определение коэффициента трансформации и КПД трансформатора можно произвести с помощью лабораторной установки, схема которой представлена на рисунке 4.

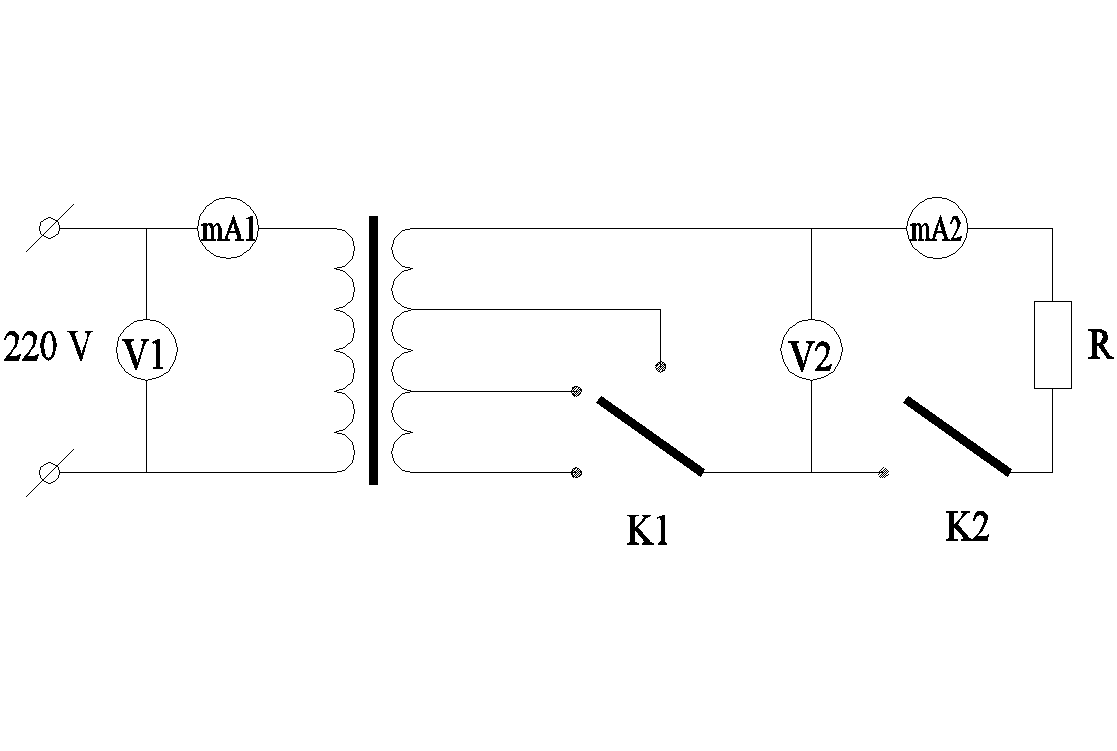
Рисунок 4- Принципиальная электрическая схема установки

В данной установке используется многообмоточный трансформатор. С помощью ключа К1 меняется напряжение на вторичной обмотке. С помощью ключа К2 устанавливается режим холостого хода. На магазине сопротивлений выставляются заданные значения активного сопротивления R. Для данного трансформатора к.п.д. определяется методом непосредственных измерений.

Программа работы

Определение коэффициента трансформации

1 Коэффициент трансформации определяется в опыте холостого хода. Для этого в цепи (рисунок 4) ключ К2 поставить в положение 1. При этом к выводам вторичной обмотки трансформатора подключается вольтметр V2 . Установить ключ К1 в положение 1. До проверки схемы преподавателем или лаборантом установку в сеть не включать!

2 Снять показания вольтметров V1 и V2 для указанных преподавателем положений ключа К1. Отключить установку от сети.

3 По формуле (2) рассчитать коэффициент трансформации для каждого положения. Полученные данные занести в таблицу 1.

Таблица 1 – Определение коэффициента трансформации

Положение ключа	1	2	3	4	5	6
U1, В
U2, В
kт

Определение КПД трансформатора

1 Установить ключ К1 в положение 1, ключ К2 в положение 2. На магазине сопротивлений выставить сопротивление 500 Ом. Включить установку в сеть.

2 Изменяя сопротивление от 500 Ом до 1000 Ом, записать показания миллиамперметров mА1 и mА2, вольтметров V1 и V2. Вычислить значения мощностей Р₁ = U₁ I₁ и Р₂ = U₂ I₂ . По формуле (3) рассчитать к.п.д. трансформатора η.

3 Повторить пункт 2 для остальных положений ключа К1. Полученные данные занести в таблицу 2.

Таблица 2 – Определение КПД трансформатора

Положение ключа	R, Ом	I1 ,А	U1, В	Р1, Вт	I1 ,А	U2, В	Р1, Вт	η

4 Сделать вывод об оптимальной работе трансформатора при различных нагрузках.

Контрольные вопросы

1 Устройство и принцип действия однофазного трансформатора.

2 Явление взаимной индукции.

3 Режимы работы трансформатора.

4 Назначение опытов холостого хода и короткого замыкания.

5 От чего зависит и как определяется КПД трансформатора.

Лабораторная работа № 4. Изучение зависимости температуры кипения воды от внешнего давления

Цель работы: изучить зависимость температуры кипения воды от внешнего давления, экспериментально определить теплоту парообразования воды.

1 Общие сведения

Жидкость может кипеть только в том случае, если внутри нее имеются газовые пузырьки, которые играют роль центров возникновения пара.

Жидкость испаряется внутрь газового пузырька. При увеличении температуры до некоторого значения объем пузырька становится таким, что нарушается силовое равновесие и пузырек всплывает, оставляя на стенке зародыш нового пузырька. Остаточный пузырек не находится в равновесии, так как внутреннее давление в нем превышает внешнее, поэтому он быстро раздувается и также всплывает. Жидкость закипает. Если жидкость кипит при постоянном внешнем давлении, то ее температура остается неизменной в течение всего процесса кипения.

Кипения жидкости можно добиться как путем изменения внешнего давления при неизменной температуре, так и путем нагревания жидкости при неизменном давлении.

В работе используется первый метод.

Попытаемся теоретически определить зависимость температуры кипения жидкости от внешнего давления.

Воспользуемся законом распределения молекул пара по энергиям. Концентрация молекул n, обладающих при равновесии потенциальной энергией U, определяется законом Больцмана

, (1)

где n_o – концентрация молекул, обладающих нулевой (по отношению к энергии U) энергией;

T – абсолютная температура;

k – постоянная Больцмана.

Это уравнение можно применить к интересующему нас случаю равновесия жидкости с соприкасающимся с ней насыщенным паром. Молекулы, покидающие жидкость при испарении, совершают работу против сил притяжения со стороны других молекул, и их энергия изменяется по сравнению с первоначальной на величину совершенной работы. Средняя энергия молекулы, вылетевшей из жидкости, отличается от энергии молекулы внутри жидкости на величину L/N_А, где L – молярная теплота испарения жидкости, а N_А – число Авогадро.

Молярная теплота испарения – это количество тепла, которое необходимо подвести к жидкости, чтобы испарить её один моль без изменения температуры (изотермически) при внешнем давлении, равном упругости ее насыщенных паров.

Величина L/N_А (за вычетом работы против внешнего давления) и есть энергия U, входящая в формулу (1). Поэтому концентрация молекул пара n_п определяется равенством

где n_ж – концентрация молекул жидкости, потенциальную энергию которых принимаем равной нулю.

Согласно формуле кинетической теории газов, концентрация молекул идеального газа связана с его давлением равенством

.

Объединяя два последних выражения, получим

. (2)

Может возникнуть вопрос о правомерности использования модели идеального газа для описания поведения пара. Более подходящим было бы здесь уравнение состояния Ван-дер-Ваальса

.

Однако, как показывают расчеты, пренебрежение членом a/V² для водяного пара при атмосферном давлении вносит погрешность < 3 % (при меньшем давлении – еще меньше), а пренебрежение b – погрешность < 0,5 %.

Таким образом, уравнение (2) определяет температурную зависимость упругости насыщенного пара с достаточно высокой точностью. При строгом рассмотрении уравнения (2) необходимо учитывать то, что входящие в него величины L и n_ж сами зависят от температуры.

Для практического использования уравнение (2) удобно переписать в виде

,

или

,

где С – константа, характерная для данной жидкости, С = ln(k^.n_ж).

Так как ln T есть медленно изменяющаяся функция температуры, то в первом приближении её можно считать постоянной величиной и включить в константу С. Тогда окончательное выражение примет вид:

. (3)

Уравнение (3) представим в следующем виде:

. (4)

Из последнего уравнения видно, что зависимость ln p от является линейной. При этом значение тангенса угла α наклона линии численно равно

. (5)

Таким образом, для экспериментального определения значения теплоты парообразования L необходимо получить зависимость давления пара p от температуры T, построить график зависимости ln p от , найти значение tgα и вычислить значение L по формуле (5).