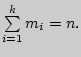- •Вопросы 9 и 10 повторяются! Здесь половина – примеры, чтобы лучше понять суть понятий. Абсолютно все учить не надо, достаточно лишь понять, что к чему. Основное я выделила.
- •Вопросы 9, 10, 11, 12
- •Выборочные характеристики вариационного ряда
- •10)Числовые характеристики, описывающие генеральную совокупность, называются параметрами.
- •12) Понятие нулевой и альтернативной гипотезы
- •Пример:
Вопросы 9 и 10 повторяются! Здесь половина – примеры, чтобы лучше понять суть понятий. Абсолютно все учить не надо, достаточно лишь понять, что к чему. Основное я выделила.
Вопросы 9, 10, 11, 12
9)Под генеральной совокупностью объектов или людей понимают множество всех мысленно возможных объектов или людей интересующего нас типа, для которых в заданных условиях изучается одни или несколько признаков или свойств. Такие объекты или люди называются элементами генеральной совокупности. Элементы одной генеральной совокупности должны обладать некоторым общим свойством, качеством, типичностью, целостностью.
Если генеральная совокупность состоит из N элементов, то N называется объемом этой совокупности. Практически объем N всегда является некоторым числом. Предполагается, что тот признак или свойство, наблюдения которых регистрируются для элементов генеральной совокупности, представляет собой некоторую дискретную или непрерывную случайную величину ξ, свойства которой описываются теорией вероятностей.
Чаще всего интересующая нас генеральная совокупность либо слишком велика, либо ее элементы недоступны, либо имеются временные, организационные, финансовые или какие-либо другие причины, не позволяющие изучить признак или свойство сразу для всех ее элементов. Тогда прибегают к изучению ξ для какой-то части этой совокупности. Эта выбранная для полного исследования признака ξ группа n < N элементов совокупности называется выборкой объема n. Выборка должна быть как бы уменьшенной копией генеральной совокупности, т. е. правильно, без искажений представлять всю генеральную совокупность. Такую выборку называют репрезентативной (представительной). Репрезентативность выборки может обеспечить чисто случайный выбор. Однако следует помнить, что и репрезентативность, и точность случайного выбора носят вероятностный характер.
Выборочные характеристики вариационного ряда
Пусть выборка задана вариационным рядом
|
|
|
. . . |
|
,
где
|
|
|
|
. . . |
|
|
Выборочным
средним
называется величина
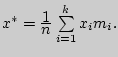
Выборочная
дисперсия
 а
корень квадратный из выборочной дисперсии
называется выборочным
средним квадратическим отклонением
а
корень квадратный из выборочной дисперсии
называется выборочным
средним квадратическим отклонением
![]()
Модой
![]() называется
вариант, наиболее часто встречающийся
в данном вариационном ряду.
называется
вариант, наиболее часто встречающийся
в данном вариационном ряду.
Медианой
![]() называется
вариант
называется
вариант
![]() такой,
что
такой,
что
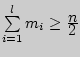 и
и
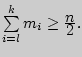 Медиана
обладает тем свойством, что сумма
абсолютных величин отклонений вариантов
от медианы меньше, чем от любой другой
величины (в том числе и от выборочной
средней).
Медиана
обладает тем свойством, что сумма
абсолютных величин отклонений вариантов
от медианы меньше, чем от любой другой
величины (в том числе и от выборочной
средней).
10)Числовые характеристики, описывающие генеральную совокупность, называются параметрами.
Под оценкой понимается любое число, рассчитанное по выборке и характеризующее параметр
Оценки подразделяются на два класса; точечные и интервальные
Точечные оценки представляют собой определенные значения параметров генеральной совокупности, полученные по выборочным данным. Эти значения должны быть максимально близки к значениям соответствующих параметров генеральной совокупности, которые являются истинными значениями оцениваемых параметров.
При формировании интервальных оценок определяют границы интервалов, между которыми с большой вероятностью находятся истинные значения параметров.
Вероятности, признанные достаточными для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называются доверительными.
Обычно в качестве доверительных вероятностей выбирают значения 0,95, 0,99 или 0,999 (их принято выражать в процентах). Перечисленным значениям соответствуют 95, 99 и 99,9 %. Выбор той или иной доверительной вероятности производится исследователем исходя из практических соображений о той ответственности, с какой делаются выводы о генеральных параметрах.
Как правило, в научных исследованиях в области правоведения считается достаточной доверительная вероятность 0,95 (95%). В некоторых случаях, когда уточняются результаты предыдущих исследований или когда выводы, сделанные в данном исследовании, связаны с большой ответственностью (например, предлагается в корне пересмотреть результаты следствия), применяются более высокие уровни доверительной вероятности: 99 или 99,9 %.
Интервал, в котором с заданной доверительной вероятностью находится оцениваемый генеральный параметр, называется доверительным интервалом.
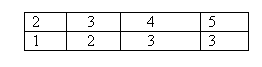
11)В том случае, когда объем наблюдений выборки небольшой, находят разные наблюдения и указывают их частоту. Полученные данные записывают в так называемую таблицу частот дискретного вариационного ряда следующего вида:

Здесь х(1) < х (2) < … < х (k) , 1≤ k ≤ n, n1 - частота х (1), n2 - частота х(2),…, nk - частота х (k), причем n1+ n2+…+nk=n.
Для вышеприведенного примера имеем таблицу следующего вида.
Рассмотрим пример. Пусть измерения роста группы школьников младшего возраста дали следующие результаты (в см): 132, 132, 133, 134, 101, 134, 135, 105, 109, 138, 138, 110, 111, 140, 115, 125, 127, 115, 116, 127, 127, 116, 117, 127, 127, 117, 128, 117, 118, 130, 119, 131, 143, 124, 124, 144, 146, 124, 125, 150, 124, 158, 125, 121, 122, 121.
Разобьем все множество результатов измерения роста на 7 интервалов вида: [101, 109), [109, 117), [117, 125), [125, 133), [133, 141), [141, 149), [149, 158]. Для каждого интервала отмечаем середину и частоту, т.е. число наблюдений, попавших в интервал. Ясно, что сумма всех частот по интервалам равна объему выборки. Кроме того, найдем и относительные частоты (частости) в интервалах, которые получаются путем деления частоты в интервале на сумму всех частот, которая в рассматриваемом примере равна 46. Ясно, что сумма всех относительных частот равна единице. Относительная частота в интервале дает процент попадания в интервал результатов измерения из их общего числа.
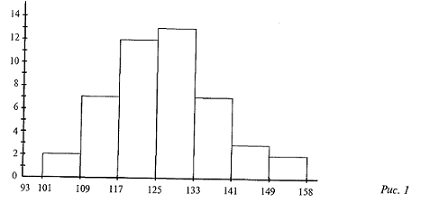
Для рассматриваемого примера получаем следующую таблицу.
Интервал |
Середина интервала |
Частота в интервале |
Относительная частота в интервале |
[101,109) |
105 |
2 |
0,0435 |
[109, 117) |
113 |
7 |
0,152 |
[117, 125) |
121 |
12 |
0,261 |
[125, 133) |
129 |
13 |
0,283 |
[133, 141) |
137 |
7 |
0,152 |
[141, 149) |
145 |
3 |
0,065 |
[149, 158] |
153 |
2 |
0,0435 |
Таблица, в которой приведены все интервалы с соответствующими частотами по интервалам для заданной выборки наблюдений, называется таблицей частот интервального вариационного ряда.
Распределения частот и относительных частот по интервалам можно представить не только в виде таблиц, но и графически. Графическое изображение данных интервального вариационного ряда строят в виде гистограммы частот или полигона частот.
Гистограмма частот изображается так: над каждым интервалом строится прямоугольник, основанием которого служит данный интервал, а высотой – частота в данном интервале. Как правило, для удобства рассмотрения единицы масштаба по оси абсцисс и по оси ординат выбираются разными. Кроме того, и начала отсчета по разным осям тоже могут не совпадать. Гистограмма частот для рассматриваемого примера показана на рис.1.
Если по оси ординат откладывать не частоты в интервалах, а относительные частоты в интервалах, то подобным образом можно построить гистограмму относительных частот.
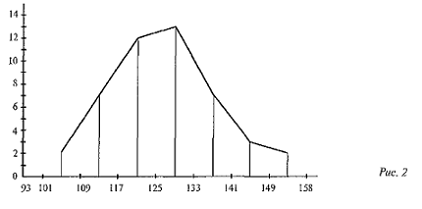
Полигон частот для интервального вариационного ряда изображается так: в середине каждого интервала строится ордината, равная частоте на этом интервале, и концы ординат соединяются. Полигон частот для рассматриваемого примера показан на рис.2.
Если же строить в середине каждого интервала ординату, равную относительной частоте на этом интервале, и соединить концы ординат, то получим полигон относительных частот.
К выборочным мерам центра распределения наблюдений случайной выборки принято относить выборочное среднее значение, выборочную медиану и выборочную моду.
Выборочное среднее значение – наиболее часто используемый показатель центра распределения наблюдений. Для наблюдений х(1), х(2),…., х(n) его обычно обозначают (или ) и определяют формулой
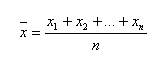
Если воспользоваться знаком Σ, то записывают в виде
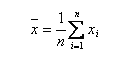
Например, если в результате опроса девяти учеников на уроке литературы получены оценки 5, 3, 5, 4, 3, 4, 2, 4, 5, то среднее значение оценок
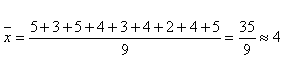
Для дискретного вариационного ряда можно использовать такую формулу
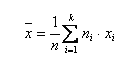
По этой формуле для предыдущего примера имеем
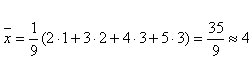
Выборочное среднее значение является наиболее важной характеристикой наблюдений выборки. Оно является центром рассеяния данных выборки. При сравнении двух выборок значений изучаемого признака, прежде всего, сравнивают между собой средние значения для этих выборок.
Если для наблюдений выборки х1, х2,…., хn построен дискретный вариационный ряд х(1), х(2),…., х(n), где х(1), х(2),…., х(n), то выборочной медианой хmed или хmed(n) называется такое число, которое делит вариационный ряд на две равные части. При этом хmed может быть наблюдением выборки, а может им не быть. Если объем n выборки нечетное число, т.е. n=2k+1, то хmed=х(к+1). Если же объем n выборки четное число, т.е. n=2k,
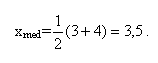
В этом случае хmed может не быть наблюдением выборки. Например, для выборки 1, 2, 3, 4, 5 имеем хmed =3, а для выборки 1, 2, 3, 4, 5, 6 имеем
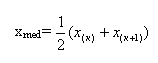
К выборочным характеристикам центра группирования, условно относят и выборочную моду хmоd. Выборочной модой хmоd называется наиболее часто встречающееся значение среди наблюдений выборки.
Например, для выборки 1, 2, 5, 5, 5, 4, 4 мода хmоd=5, а для выборки 1, 2, 5, 5, 5, 4, 4, 4 имеем две моды x(1)mod=5 ,x(2)mod=4. Таким образом, в отличие от и хmed выборочная мода хmod может быть не единственной. В таких случаях говорят об одномодальном, двухмодальном и т.д. распределении наблюдений выборки.