|
10 Пусть на пр.[a;b], где а<b задана ф-ция y=f(x). Кривая (AB)– график этой ф-ции. Выполним 5 действий. 1.Разобьем пр.[a;b] (а<b) точками х0=a<x1<x2<…<xk< xk+1< xn=b Произвольным образом на n частей. Δxk=xk+1 – xnk Δxk – частичного участка [xk;xk+1] обозначим λ=sup{Δxk} – наибольший из длин частичных участков и наз-ся λ ранг дробления. 2. На [xk;xk+1] возьмем ξk xk< ξk <xk+1 и вычислим в ней значение ф-ции.f(ξk) 3.Составим произведение f(ξk)*Δxk, (т.е. S прямоуг. заштрихов.) 4. Составим интегральную сумму. (Сумма Римана) σn=Σn-1k=0 f(ξk)*Δxk 5.Измемльчая дробление и устремляя ранг дробления к 0 I=Limσn, n→0 λ→0. Если Lim сущес. и не зависит от способа дробления и от ξk то он наз-ся определенным интегрлом ф-ции y=f(x) на [a;b] и обозначается так: I=a∫bf(x)dx a-нижний предел интегр-вания; b-верхний прдел инт-ия. Геометрический смысл. Если интеграл ф-ции f(x)>0 на пр.[a;b] то определен.интеграл дает S кривол.трапеции ограничен.отр.[a;b]сверху кривой y=f(x) а так же вертикальными прямыми x=a и x=b. Теорема существования. Опр.Ф-ция f(x) наз-ся кусочно-непрерывной на данном пр.[a;b], если она на данном пр.ограничена и имеет лишь конечное число точек разрыва. Геометрически кусочно-непрерывную ф-цию можно изобразить линией, состоящей из конечного числа непрерывных участков. Очевидно, что ф-ция, непрерывна на пр.[a;b], является частным случаем кусочно-непрерывной й-ции. Приведем теперь без док-ва теорему существования определнног оинтегрла. Теорема: Если ф-ция f(x) кусочно-непрервна на пр. [a;b], то на этом пр-ке она интегрируема, т.е. существует a∫bf(x)dx.
|
7. Вычисление обьема тел вращения с помощью определенного интеграла. Рассмотрим некоторое тело, вытянутое вдоль оси Ох(хЄ[а,b]) и допустим, что мы знаем площадь сечения этого тела любой плоскостью х=с. Обозначим площадь этого сечения через F(x). Разобьем отрезок [а,b] произвольным образом на n частей точками x0=a<x1<…<xk<xk+1< <…<xn=b. На каждом частичном участке возьмем произольную точку ξk и проведем через нее сечение, перпендикулярное к оси Ох. Площадь этого сечения F(ξk). Элементарный обьем ΔVk=F(ξk)*Δxk. Тогда очевидно, что за обьем рассматриваемого тела можно принять V=a∫bF(x)dx. В частности, отсюда нетрудно получить формулу для обьема тела вращения, которое получается от вращения кривой у=f(x) вокруг оси Ох (f(x) предпологается непрерывной на [а,b]. Действительно, в этом случае сечение предстивляет собой круг радиуса R=f(x). Следовательно, площадь сечения πf2(x). А тогда обьем тела вращения V=πa∫bf2(x)dx |
y'=c1’(х)y1(x)+c2’(х)y2(x)+c1(х)y1’(x)+c2(х)y2’(x); c1’(х)y1(x)+c2’(х)y2(x)=0; y''=c1’(х)y1''(x)+c2’(х)y2''(x)+c1(х)y1’(x)+c2(х)y2’(x);L[y1(x)]=0;L[y2(x)]=0; y1 –удовлетворяет ур-ию **. Y1''+py1'+qy1=0 Подставим y,y',y'' в *. c1’y1'+c2’y2'+c1’y1''+c2’y2''+ +c1py1'+c2py2''+c1qy1+ c2qy2=f(x); c1(y1’’+py1’+qy1)+c2(y2’’+py2’+qy2)+c1’y1'+c2’y2'; y1’’+py1’+qy1= y2’’+py2’+qy2=0; => c1’y1'+c2’y2'=f(x); Т.о. получим ограничения для искомой ф-ции с1(х) и с2(х). { c1’y1(x)+c2’y2(x)=0 c1’y1’(x)+c2’y2’(x)=f(x) }По отношению c1’(x) и c2(x) полученная система представляет собой линейную алгебраическую систему.c1(x)=∫c2’(x)dx+=c1; c2(x)=∫c1’(x)dx+=c2 Определитель алгебр.системы y1(x) y2(x) ≠0 Для каждого хЄ]a;b[, т.к. определительy1'(x) y2'(x) Вронского составленный для y1(x) и y2(x) (где y1(x) y2(x) фундам.сист.реш.; c1’ и c2’ определяются однозначно.) выполнив интегрирование найдем c1(x) и c2(x) и вернем их в соотношение ****. Т.о. получим общее решение исходного ур-ия *. Замечание: Провели док-во для ур-ия 2-го порядка. Аналогично можно доказать для ур-ия 3-го порядка, получим { c1’y1(x)+c2’y2(x)+c3’y3(x)=0; c1’y1’(x)+c2’y2’(x)+c3’y3’(x)=0; c1’y1’’(x)+c2’y2’’(x)+c3’y3’’(x)=f(x) }
|
|
8. Несобственный интеграл 1 рода (по бесконечному промежутку) 10 Опр: Допустим, что ф-ция y=f(x) орпделена на [a;+∞[ и интегрируема на каждом конечном пр.[а,А], А<+∞. Несобственным интегралом от ф-ции f(x) на пр.[а,+∞[ наз-ся lim A→+∞ a∫Af(x)dx. Обозн.несобств.интеграл: a∫+∞f(x)dx. т.е. Def:a∫+∞f(x)dx=lim A→+∞ a∫Af(x)dx. Если предел существует и конечен, то говорят, что несоб. интеграл сходится, в противном, говорят, что он расходится. Если ф-ция f(x)>0, то такой несобств. Интеграл дает S бесконеч.криволинейной трапеции. Если подинтегр.ф-ция интегрируема на пр[а,b] и оба предела бесконечны, то +∞∫+∞f(x)dx=+∞∫аf(x)dx+ а∫+∞f(x)dx. Разделим точной а. Def: +∞∫аf(x)dx=lim В→ - ∞ В∫аf(x)dx а∫+∞f(x)dx=F(x)|а+∞ =lim x→+∞ F(x) – F(a); lim x→+∞ F(x)=F(+∞);а∫+∞f(x)dx=F(+∞) – F(a). Замечание: Если нужно вычислить несобственный интеграл на верх.и нижнем пределе интегрирования, то в начале надо представить в виде суммы 2-ух слагаемых, а затем вычислить отдельно каждое слогаемое. Абсолютная сходимость. Теорема: Ф-ция f(x) определена и интегрируема на пр [а,+∞[ и при этом сходится несоб. Интеграл а∫+∞|f (x)|dx, то тогда и не собствен. интеграл а∫+∞f (x)dx наз-ся абсолютно сходящим. Первый признак сравнения. [a,b]<[a;+∞[ интегралы ф-ции φ(х) и ψ(х) и при этом для каждого х хЄ[а,+∞[: φ(х)≤ψ(х). Если сходится интеграл а∫+∞φ(x)dx, то сходится а∫+∞ψ(x)dx. Если а∫+∞φ(x)dx расходится, то расходится а∫+∞ψ(x)dx. Если r<1, то а∫+∞dx/xr расходится. Второй признак сравнения. Если φ(х) и ψ(х) определены и интегрируемы на [a;+∞[, если φ(х)>0 и ψ(х)>0, то limx→+∞φ(х)/ψ(х)=r, 0<r<+∞, то тогда необственный интеграл а∫+∞φ(x)dx а∫+∞ψ(x)dx в смысле сходимости ведут себя одинаково. |
||
|
14. Система дифференциальных уравнений, теорема существования и единственность общего решения. Метод исключения. Рассм-им систему {dy1/dx=f1(x,y1,y2,…,yn) dy2/dx=f2(x,y1,y2,…,yn)……dyn/dx=fn(x,y1,y2,…,yn)} * 1-ый порядок. y1(x),y2(x),…,yn(x) – искомые ф-ции. Если каждое ур-ие системы имеет 1-ый порядок и разрешено относительно производной и записано в виде *, то говорят, что оно разрешено относительно производной; нормальная форма Коши. х – независимая переменная. На практике t – время. Dyi/dt=y.1. . – означает дифференцирование. Теорема: Правые части системы диффер-го ур-ия записанной в нормальной форме Коши. f1(x,y1,y2,…,yn); f2(x,y1,y2,…,yn);…fn(x,y1,y2,…,yn) Д(n+1) [(x,y1,y2,…,yn)]ЄД. Если записано в нормальной форме Коши 1. Непрерывны 2. Непрерывны частные производные. ∂fi(x,y1,y2,…,yn)/∂xn (i=i,n; k=i,n), то тогда в окрестности т.х0 существует частное решение y1=φ(x), y2=φ(x),…, yn=φ(x) φ1(x)|x=x0=y10; φ2(x)|x=x0=y20;…; φn(x)|x=x0=yn0. Причем это решение является единственным. Для системы диффер-ых ур-ий вводится понятие общих решений ф-ции: {y1=y1(x,c1,c2,…,cn); y2=y2(x,c1,c2,…,cn);…; yn=yn(x,c1,c2,…,cn)}Наз-ся общим решением диффер.ур-ия, если при любом значениях произвольных постоянных эти ф-ции удовлетворяют системе дифф-ых ур-ий, кроме того имеющих смысл начальных условий констант С; определяются однозначно, при фиксирован.значениях Сio набор этих ф-ций бает нам частное решение. С геометрической точки зрения частное решение – наз-ся интегральной кривой, общее решение имеет семейство интегральных кривых. Заметим, что исключая неизвестные каждую систему n-го порядка можно свести к одному ур-ию n-го порядка. Метод исключений. Интегрирование линейных однородных систем обыкнов.диффер.ур-ий с постоянным коэффициентами в матричном виде. {dx1/dt=a11x1+a12x2+…+ a1nxn; dx2/dt=a21x1+a22x2+…+ a2nxn;…;dxn/dt=an1x1+an2x2+…+ annxn;} записан в нормальной форме Коши. Каждое aij=const. Введем в рассмотрение матрицы. | а11 а12 … а1n | | x1 | | x1 | A= |а21 а22 … а2n | x = | x2 | dx/dt= | x2 | | ……………...| | … | | … | | аn1 аn2 … аnn | | xn | | xn | X . = A*X (X . – X c точной на верху) Проинтегрируем ее в матричном виде. Будем искать частные решения методом подстановки Элера ,где X=γeλt γ=( γ1 γ2 … γn)- матрица записана в столбик!!! X . =γλeλt γλeλt=Аγλeλt => Аγ=γλ γ – собственный вектор матрицы А. (А-λЕ)γ=0 det(А-λЕ)=0 – характеристическое ур-ие. λ1, λ2,…λn. – позволяет найти фундамент решения системы:{Х1= γ(1)еλ1t;Х2= γ(2)еλ2t;…;Хn= γ(n)еλnt; } Общее решение системы: Х=С1х1+С2х2+…+Сnхn – решение в матричном виде.
|
||
|
1. a ∫af(x)dx=0 2. a∫bf(x)dx= - b∫af(x)dx это очевидно, если обратится к интегр-ой Σ для левого и правого интеграла. Для правого мы дробим с права на лево Δxk будет отличаться знаком. 3. a∫b[f1(x) + f2(x)]dx=a∫bf1(x)dx + a∫bf2(x)dx Для док-ва достаточно перейти к инте-ой Σ: Σ(f1+f2)=Σf1 + Σf2 4. a∫b[c1f1(x) + c2f2(x)]dx=c1a∫bf1(x)dx + c2a∫bf2(x)dx 5. Отр.[a;b] разбить на отерзки т.С, то при любом расположении т.а,b,с справедливо равенство: a∫bf(x)dx= a∫сf(x)dx + с∫bf(x)dx 6. Оценка опр-ого инт-ла. Т: если y=f(x) непрерывна на пр.[a;b], то на этом пр-ке справедлива такая оценка опред.интегр. m(b-a)<= a∫bf(x)dx<=M(b-a) Док-во: Т.к. y=f(x) непрерывна на пр.[a;b], то на нем она ограничена, т.е. существ. m,M: m≤f(x)≤M. Проинтегрируем почленно: a∫bmdx<=a∫bf(x)dx<=a∫bMdx; a∫bmdx=ma∫bdx=m(b-a); a∫bMdx=Ma∫bdx=M(b-a); m(b-a)<=a∫bf(x)dx<=M(b-a) 7. Если на пр[a;b]: φ(х)<=ψ(х) a∫bφ(x) <= a∫bψ(x) 8. Теорема о среднем. Если y=f(x) непрерывна на пр.[a;b], то в нутри пр. найдется т. ξ: a<ξ<b, для которой будет выполнено соотношение: a∫bf(x)dx=f(ξ)(b-a), ξ – средняя точка. С геометр. точки зрения: площадь криволинейной трапеции, ограниченной y=f(x), осью ОХ и х=а, х=b. Док-во: Т.к. ф-ция f(x) непрерывна на пр.[a;b] => в силу т.Веерштрасса о св-вах непрер-ых ф-ций она достигает наиб.и наим. m и M. m≤f(x)≤M; m(b-a)≤a∫bf(x)dx≤M(b-a) m≤1/(b-a)a∫bf(x)dx≤M. В силу т.Коши (принимая 2 каждых значения ф-ция принимает промежуточные) Существует ξ: f(ξ)=1/(b-a)a∫bf(x)dx => a∫bf(x)dx=f(ξ)(b-a) 9. Интегрирование не нарушится если в некоторых точках пр.[a;b] изменить значение подинтегральной ф-ции. |
||
|
9. Несобственный интеграл 2 рода (от бесконечной функции по конечному промежутку). Определение. Пусть ф-ция f(x) непрерывна на пр.[a;+∞[ и в точке b не ограничена, т.е. в этой точке имеет бесконечный разрыв: limf(x)=∞ при х→b-0. Несобственным интегралом второго рода а∫bf(x)dx наз-ют предел lim ε→+0 а∫b - εf(x)dx. Несобственный интеграл а∫bf(x)dx наз-ся сходящимся, если указанный предел конечен, а расходящийся в противном случае. Аналогично определяется несобстевенный интеграл, если f(x) не ограничен в точке а: а∫bf(x)dx= lim а+ε ∫bf(x)dx при ε→0. Если f(x) не ограничена на обеих концах пр.]a,b[ или во внутренней точке с (a<c<b), то несобственный интеграл определяется равенством а∫bf(x)dx=а∫сf(x)dx+с∫bf(x)dx. При этом интеграл а∫bf(x)dx считается сходящимся, если сходятся оба интеграла, стоящие справа, и расходящиеся, если расходится хотя бы один из этих интегралов. Для несобственных интегралов 2-го рода сохряняется в силе понятия: 1.сходимости в смысле главного значения. 2. Абсолютная сходимость 3. Признаки сходимости. Если а∫bf(x)dx яв-ся несобств.на верхнем и нижнем пределе интегрирования, то а∫bf(x)dx= а∫сf(x)dx+с∫bf(x)dx, где а<с<b. Сходимость же в смысле главного значения. а∫bf(x)dx=limε→+0 а+ε∫b - εf(x)dx. Абсолютная сходимость а∫b|f(x)|dx влечет за собой сходимость а∫bf(x)dx. Эталонный интеграл I= а∫bdx/(x-b) r является несобственным на верхнем пределе интегрирования. Нетрудно показать, что интеграл сходится, если r<1,и расходится, если r>=1. Док-во сама |
||
|
Теорема об интеграле с переменным верхним пределом. Если f(x) непрерывна на пр.[a;b], то тогда произв.от интеграла с переменным вверхним пределом от ф-ции f(x) поэтому верхнему пределу равно подинтегральной ф-ции вычисленной в точке дифференцироввания. (a ∫ х f(x)dx)'х = f(x) Док-во: Введем в рассмотрение ф-цию Ф(х), Ф(х)=a ∫ х f(x)dx. С геометрической точки зрения ф-ция Ф(х) дает S кривой трапеции ограниченной отр.[a;x], а сверху y=f(x). Дадим приращение Δx . Ф(х+Δx)=a ∫ х+Δx f(x)dx=a ∫ хf(x)dx+ х ∫х+Δx f(x)dx; a ∫ хf(x)dx = Ф(х); ΔФ(х)=Ф(х+Δx)–Ф(х)=х ∫ х+Δx f(x)dx кпослед.интегр. применим т.о среднем х ∫ х+Δx f(x)dx =f(ξ)*Δx;(x≤ξ≤x+Δx;) ΔФ(х)\Δx=f(ξ) устремим Δx->0. Точка ξ зажате м\у х и x+Δx тоже ξ→0, т.к. ф-ция f(x) непрерывна, то Limf(ξ)ξ→x=f(x). LimΔx→0ΔФ\Δx = Ф’х(x), Ф’х(x)=f(x) или вспоминая что такое Ф(х) мы окончательно получим: (a ∫ хf(x)dx)’x=f(x). ч.т.д. |
||
|
!!!!10. Дифференциальные уравнения 1 порядка. Общее решение, общий интеграл, частное решение, теорема существования и единственности решения, задача Каши. Общие сведения: Рассмотрим ур-ия F(x,y(x),y’(x))=0 y(x)-искомая ф-ция; x-аргумент. Т.к.уравнениеие содержит производную, то оно наз-ся дифференциальным. Обыкновенное содержит обыкновенные производные, порядок дифференц-ого ур-ия определяется порядком старшей производной. Решением диффер-ого ур-ия явлеяется всякая ф-ция удовлетворяющая его условию. Если задача интегрирования дифф.ур-я сведена к интегралам, то говорят, что получено решение в квадратурах. Ур-е F(x,y,y’)=0 связывающее независимую переменную x искомую ф-ю y(x) иее производную наз-ся обыкновенным дифференциальным уравнеием 1-го порядка. Если ур-ие удается разрешить относительно 1-й производной, т.е. записать y’(x)=f(x,y) – нормальная форма Коши. dy/dx=f(x,y). Теорема: (Существования и единственность решения обыкновенного дифференциального ур-я 1-го порядка). Если в окрестности некоторой точки (х0,у0) ф-ция f(x,y) удовлетворяет следующим условиям: 1.f(x,y) – непрерывна. 2. Частная производная ∂f(x,y)/∂(y) непрерывна, то существует единственное удовлетворяющее решение y|x=x0=y0. Пример: y’=x; y(x)=x2/2+C; интегральная кривая. y=y(x,C). Мы получили семейство решение, которое содержит постоянную, такое решение наз-ся общим. Если не удается найти y, как y=y(x,C), а удается только найти соотношение I(x,y,C)=0. Оно наз-ся общим решением. Соотношение I(x,y,C)=0, определяющее решение, как неявню ф-ю наз-ся общим интегралом диффер. ур-я. Часным решением диф.ур-я называют любое решение, которое содержится в семействе его общего решения при фиксированном значении его произвольной постоянной.Однако у диффер.ур-я существуют решения, которые не содержат с, такие решения наз-ся особыми Задача Коши: (задача отыскания частного решения). Решить задачу Каши для y=f(x,y) – это значит найти решение y’=f(x,y) удовлет.условию y|x=x0=y0. В семействе интегральных кривых выделяют кривую проходящую через (x0,y0). Задача сводится к отысканию производной постоянной. y′=3y2/3 общее решение y=(x+c)3 – семейство кубических парабол. сущ-ет так же решение y=0 – особое решение |
||
Рассмотрим систему линейных однородных уравнений первого порядка с постоянными коэфициентами
Если собственные числа 1,2,... n различны, то найденные вектора X1,X2,...Xn линейнонезависимы, а функция X(t)=c1(1)*e1t+ c2(2)*e2t+...+ cn(n)*ent, где с1,с2,... сn – произвольные постоянные, является общим решением прассмтриваемой системы, причем в этом семействе содержиться любое решение, удовлетворяющее условиям x1(t0)=x10, x2(t0)=x20,... xn(t0)=xn0. |
||
|
4. Вычисление опред-ного интегрла. Формула Ньютона – Лейбница. Теорема Барроу (см. билет 3)- это вычисление определенного интеграла. Теорема Барроу: Если ф-ция f(x) непрерывна на пр.[a;b], то определенный интеграл от этой ф-ции по пр. [a;b] равен разности значений какой-либо первообразной этой ф-ции на верхнем и на нижнем пределах интегрирования, т.е. a ∫ хf(x)dx в силу теоремы об интеграле с переменным верхним пределом также является первообразной для ф-ции f(x). Положим в этом равенстве x=b, тогда будет a ∫ bf(x)dx=F(b)+c. Пологая же в нем x=a, получим a ∫ аf(x)dx=F(а)+c откуда следует, что с=-F(а), т.к. a ∫ аf(x)dx=0. Заменяя в предыдущем равенства с на -F(а), получим окончательно a ∫ bf(x)dx=F(b)-F(а). Эта формула наз-ся формулой НЬЮТОНА-ЛЕЙБНИЦА. Итак, для того, чтобы вычислить определенный интеграл, достаточно вычислить разность значений первообразной в двух точках. Заметим, что разность F(b)-F(а) обозначают так: a ∫ bf(x)dx= F(х)|ab=F(b)-F(а). Замечание: 10 Граф.четной ф-ции симметрич.относит.ОУ.На этом основании мы ограничемся вычисление половины площади. -а ∫ аf(x)dx=2 0 ∫ аf(x)dx, если f(x)-четная. 20 Если f(x)-нечетная, то граф.симметричен относительно начала координат. –а ∫ аf(x)dx=0. |
||
|
Пусть кривая АВ задана уравнением у=f(x), где х[a;b]. Предположим, что ф-ция f(x) и ее произовдная f ’(x) Непрерывна на [a;b]. Разобьем кривую АВ точками следующим друг за другом, на n частей и впишим в нее ломаную линию. Длиной дуги кривой АВ мы будем наказывать предел длины вписанной в нее ломаной линии при условии, что n→∞, а длина наибольшего звена ломаной стремится к нулю. Обозначим длину частичного участка ломаной линии lk=[(Δxk)2+(f(xk+1)-f(xk))2]1/2.Преобразуем здесь по формуле Лагранжа разность f(xk+1)-f(xk). Получим f(xk+1)-f(xk)=f ’(ξk)*Δxk, xk≤ξk≤xk+1, тогда lk=[1+(f ’(ξk))2]1/2*Δxk. Длина всей ломаной ln=Σn-1k=0[1+(f ’(ξk))2]1/2*Δxk. Это есть интегральная сумма для непрерывной ф-ции (1+f ’2(х))1/2. Измельчая дробление и устремляя ранг дробления к нулю, в пределе получим такое выражение для длины дуги плоской кривой. L=a ∫ b(1+f ’2(х))1/2dx. Если кривая задана параметрическими ур-ниями x=φ(t) y=ψ(t), причем при возрастании параметра от α до β точка М[φ,ψ] описывает всю кривую, то длина дуги вычисляется по формуле L=a ∫ b[(φ’(t))2+ (ψ’(t))2)1/2dt. Заметим, что здесь естественно предпологается что ф-ция φ(t) и ψ(t) и их произодные непрерывны на пр.[α,β]. Если кривая АВ задана уравнением в полярных координатах r=r(φ), где ф-ция r(φ) непрерывна на пр.[α,β], то нетрудно получить формулу для вычисления длины дуги кривой АВ, воспользовавшись только что выведенной формулой. Действительно, можно принять φ за параметр, тогда получим такой частичный случай параметрического ур-ия кривой АВ: х=r(φ)cosφ, y=r(φ)sinφ, yЄ[α,β]. Отсюда [x’φ]2+[y’φ]2= =r2[φ]+[r’(φ)]2. Т.о., окончательно имеем: L=α ∫ β[r2(φ)+ (r’(φ))2)1/2dφ. |
||
|
11. Линейное однородное уравнение n-го порядка. Теорема о структуре общего решения Линейным однородным дифернциальным ур-м n-го орядка наз-ся ур-е вида y(n)(x)+p1(x)y(n-1)(x)+p2(x)y(n-2)(x)+...+ pn(x)y(x)=0 Теорема о структуре общего решения Совокупность n решений линейного однородного ур-я n-го порядка, определенных и линейно независимых на интервале ]a,b[ наз-ся фундаментальной системой решения на этом интервале. Теорема: Если y1(x),y2(x)....yn(x) – фундаментальная система решений ур-я y(n)(x)+p1(x)y(n-1)(x)+p2(x)y(n-2)(x)+...+ pn(x)y(x)=0, то выражение y― =c1y1(x)+c2y2(x)+c3y3(x)+...+ cnyn(x), где с1,с2,с3,......сn – произволные числа дает общее решение ур-я. Док-во:
|
||
|
12. Теорема о структуре решения линейного неоднородного уравнения n-ного порядка. L[y]=f(x); L[y]=0; y1(x),y2(x),…yn(x). – фундаментальная система решений. Общее решение этого ур-ия: y—= c1y1(x)+c2y2(x)+…+cnyn(x).(!!! y—–это у с подчеркиванием сверху!!!) Теорема: Общее решение ур-ия L[y]=f(x) имеет вид y=y—+y*; y—=c1y1(x)+c2y2(x)+…+cnyn(x) представляет собой общее решение линейного однородного ур-ия. у* представляет собой частное решение исходного ур-ия. L[y*]=f(x). Замечание: Если правая часть f(x)=f1(x)+f2(x), то частное решение у* имеет вид: y*=y1*+y2* y1*–час.реш. L[y]=f1(x); y2*–час.реш. L[y]=f2(x)
|
||
|
Рассмотрим на пл.хОу некоторую кривую АВ, заданную ур-ием у=f(x) (f(x)>=0), хЄ[а,b]. Пусть ф-ция f(x) и произовдная f’(x) непрерывна на пр.[а,b]. От вращении кривой АВ вокруг оси Ох получится поверхность вращения. По определению будем считать площадью поверхностного вращения площадь поверхности, которая получается от вращения ломаной линии А=А0,А1,…,Аn=В, вписанной в кривую АВ. От Вращения хорды АkAk+1 получим усеченный конус, Боковая поверхность которого ΔSk≈x[f(xk)+f(xk+1)]lk≈ ≈2πf(ξk)[1+(f ’(ξk))2]1/2**Δxk, где xk≤ξk≤xk+1. Площадь поверхости вращения S таким образом, приблизительно равна S=Σn-1k=02πf(ξk)[1+(f ’(ξk))2]1/2**Δxk. Измельчая дробление и устремляя ранг дробления к нулю, получаем точное равенство S=2πa∫bf(x)[1+(f ’(x))2]1/2dx |
||
|
13. Метод вариации Лагранжа. Интегрирование уравнения вида L(y)=f(x) Метод вариац. Лагранжа обобщается на ур-ия вида: y(n)+p1(x)y(n-1)+p2(x)y(n-2)+…+pn(x)y=f(x) Линейное неоднородное ур-ие с переменными коэффициентами и правай часть f(x) любая ф-ция не обязательно специального вида лишь бы она удовлетворяла теореме существования. Суть метода и док-во приведем для ур-ия 2-го порядка. y'’+p(x)y’+q(x)y=f(x)*. p(x) и q(x) – переменные коэффициенты. f(x) – любая. Метод Л.дает общий способ интегрирования. Требуется, чтобы однородные ур-ия можно было проинтегрировать. Найти фундаментальную систему решений. y1(x),y2(x) - фундам.система реш. L[y]=0 ** y—=c1y1(x)+c2y2(x).*** Проварируем произвольные постоянные c1,c2,т.е. будем искать ур-ие . y=c1(х)y1(x)+ +c2(х)y2(x)**** Ф-ции подлежащие ур-ию c1(х),c2(х) наложить некоторые ограничения чтобы эти ф-ции находились бы однозначно. |
Основные понятия. Опр1: Некая кривая К расположена в пл.хОу наз-ся простой кривой, если она расподается на конечное число частей, каждая из которых имеет ур-ие: y=φ(x); xЄ[а,b]; x=ψ(y); yЄ[c,d]. Причем φ(x) ψ(y) непрерывны на пр. [а,b] и[c,d]соответственно(рис1). Опр2: Область Д наз-ся простой если ограничена простой кривой(рис2). Опр3: Диаметром области Д наз-ся наибольшее из расстояний между точками лежащими на границе области Д. d=sup{r(M,N)} Будем рассматривать простые области(рис3). |
|
1.Определенный
интеграл. Определение, теорема
существования, геометрический смысл.
2.Св-ва
опред-ного интегрла. Теорема об оценке
опред-ного интегрла и теорема среднем.
3
.Теорема Барроу.
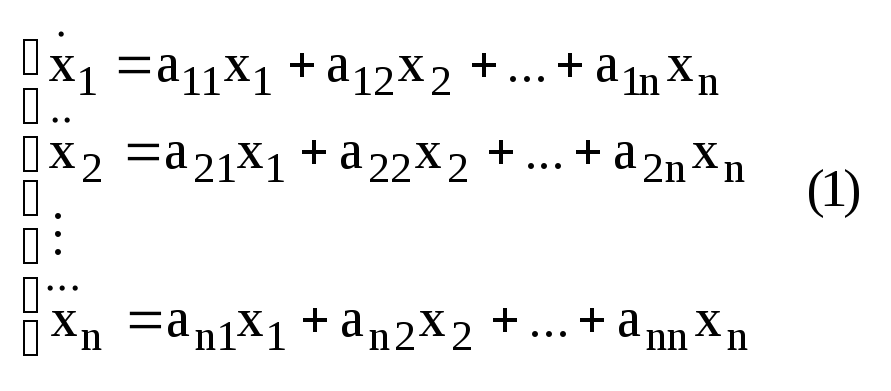Введем
в рассмотрение такие матрицы :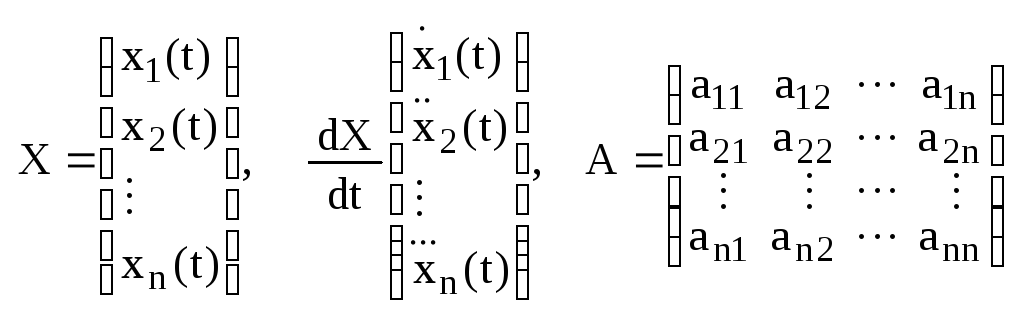
Систему
(1) можно записать в векторно-мтричной
форме:
dX/dt=A*X
(2) Решение системы будем искать в виде
X=*et
-вектор-столбец,
подлежащий определению, причем
i=const
(i=1,2..n).
Тогда x=et
Подставим
в
систему (2), получим et=Aet
Это
равенство может быть верныт только
когда =
A.
Ненулевой вектор ,
удовлетворяющий такому условию
назывется собственным вектором матрицы
А. Тогда имеем (А-Е)*=0.Это
уравнение наз-ся характеристическим.
Решая его получим собственные числа
1,2,...
n
и соответствующие им собственные
вектора
,
,
...
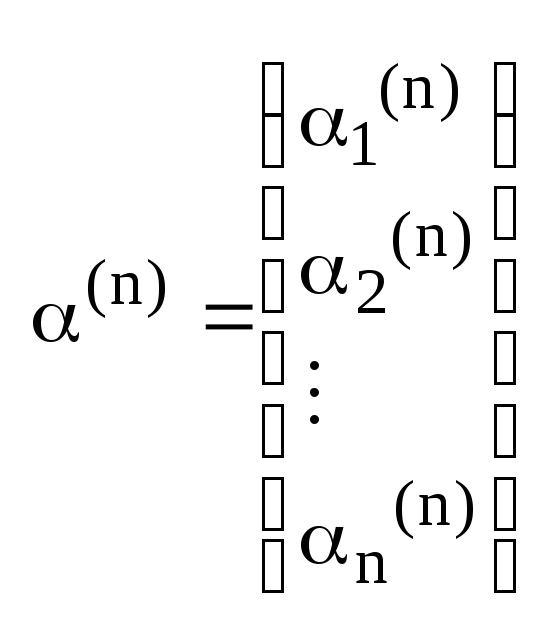А
тогда можно написать соответствующие
часные решения исходной системы.
,
,...
5.
Вычисление длины дуги плоской
кривой с помощью определенного
интегрла.
6.
Вычисления
площади поверхности тел вращения с
помощью определенного интеграла.