
|
Пусть в плоскости x0y задана некоторая кривая АВ, причем а<b и в каждой ее (.) определена f(x,y) Выполним 5 операций 1.Разобъем кривую АВ точками M0=A, M1, M2...Mk....Mn=B обозначив d=d1 d2 d3 ...dn длины хорд, стягивающих дуги =sup{dk} назовем рангом дробления. 2.Возьмем в каждом участке [Мk Mk+1] (.) и вычислим в ней значение функции. 3.Составим произведение f( k ,k )*dk 4.
Составим интегральную сумму n= 5.Измельчая
дробление и ранг дробления ищем
I=lim n
(n∞,∞)
Если
этот предел существует и независит
от способа дробления и выбора k
,k,
то он называется криволинейным
интегралом дуге I= Теорема существования. 1.Пусть кривая AB задана параметрическим уравнением x=(t), y=(t) {t[p;q]},где ф-и (t), (t), (t) и (t) определены и непрерывны на [p,q] 2.
Пусть в каждой (.) АВ f(x,y)
неперывна, тогда крволинейный интеграл
1 рода пол кривой АВ J= Часный случай т.Существования (Если АВ задана явным уравнением y=(t), x[a;b] ) 1. Если АВ задана явным уравнением y=(t), x[a;b] : (t) и (t) непрерывны 2.
Функц. f(x,y)
непрерывна
в каждой (.) АВ , то тогда криволинейный
интеграл 1-го рода по АВ существует и
выражается так :
Свойства (вытекают из св-в определенного т.к. он выр-ся через определен.) 1. a ∫af(x)dx=0 2. 3.
4.
5.Отр.[a;b]
разбить на отерзки (.)С, то при любом
расположении т.а,b,с справедливо
равенство:
6.Оценка
опр-ого инт-ла. Т: если y=f(x) непрерывна
на пр.[a;b], то на этом пр-ке справедлива
такая оценка опред.интегр. m(b-a)
т.е. существ. m,M: m≤f(x)≤M. Проинтегрируем почленно:
аналогично и (.) М 7.Если
на пр[a;b]: φ(х)ψ(х)
8.Теорема
о среднем. Если y=f(x) непрерывна на
пр.[a;b], то в нутри пр. найдется т. ξ:
a<ξ<b, для которой будет выполнено
соотношение:
Док-во: Т.к. ф-ция f(x) непрерывна на пр.[a;b] => в силу т.Веерштрасса о св-вах непрер-ых ф-ций она достигает наиб.и наим. m и M. m≤f(x)≤M; m(b-a)≤
9.Интегрирование не нарушится если в некоторых точках пр.[a;b] изменить значение подинтегральной ф-ции.
25. Криволинейные интегралы 2 рода, определение, теорема существования. Свойства. Пусть в плоскости x0y задана некоторая кривая АВ, причем а<b и в каждой ее (.) определена f(x,y) Выполним 5 операций 1.Разобъем кривую АВ точками M0=A, M1, M2...Mk....Mn=B Этому разбиению соответствет разбиение АВ на x0<a<x1<x2...xk-1<xk...<xn<b xk= (xk-1-xk) =sup{x k} назовем рангом дробления. 2.Возьмем в каждом участке [Мk Mk+1] (.) и вычислим в ней значение функции. 3.Составим произведение f( k ,k )* xk 4.
Составим интегральную сумму n= 5.Измельчая
дробление и ранг дробления ищем
предел I=lim n
(n∞,∞)
Если
этот предел существует и независит
от способа дробления и выбора k
,k,
то он называется криволинейным
интегралом дуге I= ЗАМ1 Принята такая запись:
ЗАМ2
Может
оказаться, что кривая АВ, по которой
ведется интегрирование представляет
собой замкнутый контур. Тогда интнграл
обозначается так:
ЗАМ3. Может оказаться, что интегрирование по кривой АВ не зависит от того, какой кривой соединины эти точки.
|
Теорема существования. 1.Пусть кривая AB задана параметрическим уравнением x=(t), y=(t) {t[p;q]},где ф-и (t), (t), (t) и (t) определены и непрерывны на [p,q] 2.
Пусть в каждой (.) АВ f(x,y)
неперывна, тогда крволинейный интеграл
2 рода пол кривой АВ J= Часный случай т.Существования (Если АВ задана явным уравнением y=(t), x[a;b] ) 1. Если АВ задана явным уравнением y=(t), x[a;b] : (t) и (t) непрерывны на [a,b] 2.
Функц. f(x,y)
непрерывна
в каждой (.) АВ , то тогда криволинейный
интеграл 1-го рода по АВ существует и
выражается так :
Свойства (вытекают из св-в определенного т.к. он выр-ся через определен.)
1.
.
2. 3.
Отр.[a;b] разбить на отерзки (.)С, то при
любом расположении т.а,b,с справедливо
равенство:
|
Теперь только достаточно обозначит замкнутую кривую AMBNA буквой L 2.Второе утверждение : Если интеграл по замкнутоиу контуру =0, то он не зависит от пути интегрирования, доказывается аналогично, для чего надо разбить контур L на 2 участка. ТЕОР1.
Для того, чтобы
Док-во (достаточность):Допустим в каждой (.) области S выпол-ся это словие. В замкнутый самоненпересекающийся контур L , целиком лежащий в области S и ограничивающий область Д. По формуле Грина:
Необходимость:
Пусть (*) не выполнено всюду в S
и найдется (.)M0
непрерывны, то можно найти круг ∆p с центром в (.)M0 сколь
угодно малого радиуса p
, что последнее неравенство действительно
во всех точках области ∆p.
Пусть L
– контур области ∆p.
Для этой области справедлива формула
Грина, но т.к. в каждой (.) области ∆p
,то
двойной интеграл
ТОР2.
Если в каждой точке области S
функции
P(x,y) и
Q(x,y)
непрерывны и имеют часные производные
и в каждой (.) выполнено условие
т.е.
Док-во: Пусть в каждой точке области S ваполняется условие (*) .Закрепим (.)A(a,b) и пусть M(x,y) – какая-либо точка в области S. Тогда интеграл
от
линии АМ. Это означает, что описанный
интеграл является функцией от
переменных x
и
y.
Обозначим его Ф(x,y),
тогда можем записать:
Выразим
криволинейный интеграл, стоящий в
правой части через определенный
интеграл, учитывая , что на MN
dy=0
, а x[x,x+x].
Тогда получим
Следовательно
ф-я Ф(x,y)
дифференцируема, причем
ЗАМ
Доказанная теорема дает возможность
находит ф-ю Ф(x,y)
по ее полному диференциалу с помощью
криволинейного интеграла .Для этого
нужно закрепить к.л. точку (a,b),
а затем взяв произвольную (.)(x,y),
соединить их к.л. кривой L
и вычислить
|
|
26.Формула Грина Пусть задана некоторая облать Д, ограниченная снизу кривой y=(x), сверху - y=Ф(x), а с боков отрезками АВ и СD, авраллельными оси oy.И пусть в этой области определена функция P(x,y)имеющая непрерывную часную производную P(x,y).
Вычислим J= к
повторному интегралу получим
Правые
части 2 последних фрпмул отличаются
только знаком
и для области Нетрудно доказать, что эта формула справедлива любой области, распадающейся на конечное число частей, изображ.на рисунках. Если в области Д определена и непрерывна функция Q(x,y), имеющая непрерывную
производную
Складывая
эти 2 полученные малые формулы Грина
получаем большую формулу Грина: Эта формула устанавливает зависимость м/у двойным интегралом по области Д и криволинейным интегралом по этой области. ЗАМ1(О вычислении полщади с помощь криволинейного интеграла.) Положим
в ф.Г. P(x,y)=
-y,Q(x,y)=x,
тогда получим. |
||
|
27. Вычисление площади плоской области, ограниченной замкнутой кривой, с помощью криволинейного интеграла. СМ БИЛЕТ № 26 Вычислим площадь эллипса x=a*cos t y=a*sin t. Очевидно, что параметр t изменяется от 0 до 2, точка (x,y) обегает полный контур эллипса в положительном направлении. Учитывая, что xt = -a*sin t yt=a*cos t Sэлл=
|
||
|
Пусть
функции Р(x,y)
и Q(x,y) определены и нерперывны в
некоторой области S
и имеют в ней непрерывные часные
производные.
ОПР1
Говорят, что интергал
ОПР2 Говорят, что интеграл по замкнутому контуру =0 если для любого замкнутого самоненпересекающегося контура L , целиком лежащего в области S.
ЛЕММА ОПР1 эквив. ОПР2. 1.Докажем, что если криволинейный интеграл не зависит от пути интегрирования, то тогда по любому замкнутому контуру он = 0.
|
||
|
? 29. Свойства криволинейного интеграла, на зависящего от пути интегрирования 1. 2.Каков
бы ни был замкнутый самонепересекающийся
контур L
3.Всюду
в S
4.Выражение
5. Ф(x,y) непрерывна т.к. P(x,y) и Q(x,y) непрерывны ( P(x,y) и Q(x,y)-непрерывны). 6.
|
|
Если с каждой точкой некоторой пространственной областью связано значение а. а→=ах(x,y,z,t)i→+ау(x,y,z,t)j→+az(x,y,z,t)k→. То говорят, что задано векторное поле или поле а. V→(x,y,z,t) Рассмотрим поле текущей жидкости. Если V жидкости в русле реки, то очевидно, что свезав с руслом реки систему координат, мы получим переменный вектор V в разных точках разные V и в разное время суток (таяние льда: V больше днем; V меньше ночью) Если V→ зависит только от x,y,z, то поле наз-ся стационарным (т.е. стационарное, если не зависит от времени). Очевидно, что задание однако векторного поля эквавалентно заданию трех скалярных полей. Опр1: Кривая l наз-ся векторной линией, если в каждой точке этой кривой вектор поля соотнесенной этой точки касается этой прямой. l – векторная линия. Если l задана параметрич. ур-ием: {x=x(t); y=y(t); z=z(t)} τ→(dx,dy,dz) τ→ – касательный вектор с координатами. Очевидно, что а→ и τ→ коллениарны. а→ =λτ→ => координаты пропорциональны. ах(x,y,z,t)/dx=ау(x,y,z,t)/dy=az(x,y,z,t)/dz – Проинтегрировав найдем семейство векторных линий. Опр2: Поверхность образован.вект.линиями проходящими через данную кривую К наз-ся векторной поверхностью. Если К замкнутая, то векторная поверхность наз-ся векторной трубкой
|
32. Формула Остроградского(вывод) Пусть в теле Т задана функция R(x,y,z), пусть задана
производная
ограничено сверху S1 , снизу S2, с боков - S3 Рассмотрим такой интеграл :
Каждый из этих интегралов – поверхосный интеграл.
Заметим,
что
т.о. мы можем выразить тройной интеграл через поверхносный.
Предполжив,
что в данном теле функции P(x,y,z) и
Q(x,y,z)
непрерывны, а так же непрерывны часные
производные
Сложим все 3 формулы почленно.
большая формула Остроградского. Формула остроградского устанавливает зависимомость м/у тройным интегралом по телу Т и поверхносным интегралом по поверхности, ограничивающей тело Т. В правой части формулы перейдем к поверхносному иетегралу 1 рода.:
|
30. Поверхносный интеграл 1 рода. Определение. Теорема существования Пусть задана некоторая поверхность S, и в каждой ее (.) определена f(x,y,z) Выполним 5 операций 1.Разобъем поверхность S сетью простых кривых на ячейки S 1, S 2... S k.... S n с площадями S 1, S 2... S k.... S n обозначив d=d1 d2 d3 ...dn диаметры этих ячеек =sup{dk} назовем рангом дробления. 2.Возьмем в каждой ячейке S (.) M( k ,k, k ) и вычислим в ней значение функции f( k ,k, k ). 3.Составим произведение f( k ,k, k )* S 4.
Составим интегральную сумму n= 5.Измельчая
дробление и ранг дробления ищем
I=lim n
(n∞,∞)
Если
этот предел существует и независит
от способа дробления и выбора k
,k
,
k,
то он называется поверхносным интегралом
1рода I= Теорема существования. 1.Пусть
пов-ть S
задана уравнением Z=f(x,y)
причем f(x,y)определена и непрерывна в
простой области D плоскости
xOy
и имеет в этой области непрерывные
часные производные
2.
Пусть в каждой (.)пов-ти
S
подинтегральная F(x,y,z)
неперывна, тогда поверхносный интеграл
1 рода от f(x,y,z)
cуществует
и выражается через определенный
интеграл так
Свойства: (совпадают со св-ми двойного интеграла) 1.
2.Если
в плоскости S
3. Оценка поверхносного интеграла 1рода. Если f(x,y,z) непрерывна на пов-ти S сущ-ет m, M:
док-во: т.к. f(x,y,z) непрерывна на пов-ти S , то она имеет наименьшее m и наибольшее M значение ,те имеют место неравенства : mf(x,y,z)M
4.
Теорема о среднем. Если f(x,y,z)
нерерывна на плоскости S,
то тогда на плоскости S
найдется точка с координатами (
, ,)
тогда
Док-во:
т.к. функция непрерывна тогда на
плоскости S,
то всилу св-ва 3 справедливо
Но
непрерывная функция, принимая любые
два значения, принимает и промежуточное.
31.Сторона поверхности.Поверхносный интеграл 2 рода. Теорема существования. Возьмем некоторую поверхность S на ней – (.)М0 и в (.)М0 построим нормаль и закрепим на ней к.л. определенное напавление. Перемещая основание нормали по к.л. кривой перейдем в (.)М, а потом возвратимся обратно, при этом не выходя за грань S Может оказаться, что после такого обхода нормаль перевернется . Если на поверхности имеется хотя бы 1 контур, переворачивающий нормаль, то такая поверхность называется односторонней. Дадим строгое определение стороны пов-ти. ОПР1. Стороной пов-ти наз-ся совокупность точек на пов-ти вместе с соответствующими направлениями нормалей, напрерывно переходящих друг в друга при перемещении основании нормали по пов-ти. Двусторонняя пов-ть имеет 2 стороны, а односторонняя пов-ть не имеет ни одной стороны. Если двусторонняя пов-ть задана ур-м Z=f(x,y), где
непрерывны в области D плоскости xOy, то для верхней стороны пов-ти(образующей острый угол с Z) направляющие косинусы нормали равны:
а для нижней стороны поверхности:
Поверхносный интеграл 2 рода. Рассмотрим двустор. пов-ть S, которая распологается над областью D плоскости xOy и пусть в каждой (.) этой пов-ти опред ф-я f(x,y,z). Выполним 6 операций: 1.Закрепим на пов-ти S к.л. сторону пов-ти – верхнюю или нижнюю. 2.Разобъем поверхность S сетью простых кривых на ячейки S 1, S 2... S k.... S n , которые проектируются на пл-ть xOy в ячейки D 1,D 2... D k....D n с площадями F 1, F 2... F k.... F n обозначив d=d1 d2 d3 ...dn диаметры этих ячеек =sup{dk} назовем рангом дробления. 2.Возьмем в каждой ячейке S (.) M( k ,k, k ) и вычислим в ней значение функции f( k ,k, k ). 3.Составим произведение f( k ,k, k )* Fk 4.
Составим интегральную сумму n= 5.Измельчая
дробление и ранг дробления ищем
I=lim n
(n∞,∞)
Если
этот предел существует и независит
от способа дробления и выбора k
,k
,
k,
то он называется поверхносным интегралом
2рода
I= точно
так же определяются и интегралы : I= I= Теорема существования. 1.Пусть
двусьоронняя пов-ть S
задана уравнением Z=f(x,y)
причем f(x,y)определена и непрерывна в
простой области D плоскости
xOy
и имеет в этой области непрерывные
часные производные
2.
Пусть в каждой (.)пов-ти
S
подинтегральная F(x,y,z)
неперывна, тогда поверхносный интеграл
1 рода от f(x,y,z)
cуществует
и выражается через определенный
интеграл так
|
|
37. Поток векторного поля. Его механический смысл. Возьмем поле вектора а а→=ахi→+ауj→+azk→ некоторую двухсторонюю поверхность S и зафиксируем одну из сторон поверхности закрепив нормаль n→. an=nρn→a→. Пусть в пределах элементарной площадки ΔS вектора a→ и n→ не меняются, т.е. ΔS – плоская и вектор есть постоян. ΔQ=anΔS – элементар.поток векторного поля а, через площадку ΔS выбранную сторону. Измельчая площадку ΔS и выполняя суммирования элементарных потоков по всей поверхностей S получим: Q=∫∫SаndS – поток векторного поля а через поверхность S в выбранную сторону.Выясним механический смысл потока векторного поля для чего рассмотрим V текущей жидкости. V→=Vх(x,y,z,t)i→+Vу(x,y,z,t)j→+Vz(x,y,z,t)k→ н Vk=прn→V→. Δt; частицы продвинуться через площадку ΔS за Δt и заполнят собой косой цилиндр высота которого Vn Δt а масса жидкости заполняющий косой цилиндр Δm=ρVnΔtΔS; ρ=ρ(x,y,z,t), где ρ – плотность жидкости. ρ=const=1. Тогда выполняя суммирование элементарных масс по всей поверхности S получим M=(∫∫( ρV)nΔS)Δt; M/Δt – количество жидкости протекающей через поверхность S за един.времени, => поверхность интегр. ∫∫( ρV)ndS дает нам кол-во жидкости протекающей через двух сторон.поверхность за единицу времени.
|
||
|
Опр: Дивергенцией векторного поля (его расходимостью) наз-ся выражение: div а→ =∂аx/∂x + ∂аy/∂y + ∂az/∂z. Механический смсл Дивергениции Замечание 1 : Механический смсл Дивергениции. Пусть тело Т мало.
∫
Если сжимать тело в точку, то из этого соотношения мы можем сделать вывод, что дивнргенция векторого поля вычислен. в точке М0 дает нам кол-во жидкости вытекающей из точечного источника за единицу времени (удельную силу источника). Если в (.)М0 div>0, то мы имеем источник в точке М0, если div<0 в т.М0 имеется сток. Замечание 2: В силу т.Остроградского: принимая во внимание, что тройной интеграл есть сумма мы можем сказать, что поток векторного поля через замкнунутую поверхность наружу равна сумме попарных произведений удельных сил точечных источников на элементарные обьемы заключающие внутри себя эти источники. |
||
|
33.Вычисление объема тела с помощью поверхносного интнграла 1 и 2 рода. Формула Остроградского позволяет легко получить формулук для вычисления объема тела Т с помощью поверхносного интеграла по поверхности, ограничивающей тело Т. Если положить в формуле Остроградского P(x,y,z)=x Q(x,y,z)=y R(x,y,z)=z, тогда плучим:
|
||
|
34.Скалярное поле. Поверхности уровня. Градиент. Оператор. Гамильтона. Если с каждой точкой некоторой пространственной области Т связано значение значение скалярной величины U(x,y,z), то говорят, что задано скалярное поле. Если мы зафиксируем значение поля, то получим множество точек для которых поле имеет постоянное значение. Такая поверхность называется поверхностью уровня. U(x,y,z)=c. Различные поверхности уровня не пресекаются и через каждую (.) пространства проходит одна из них. Допустим поле не имеет особых точек. Рассмотрим поверхность уровня U(x,y,z) Нормаль к U(x,y,z) в (.)М0 (x0,y0z0) имеет координаты:
Очевидно, что градиент скалярного поля перпендикулярен к поверхности уровня в каждой ее точке. Градиент – векторная хар-ка скалярного поля. С помощью оператора Гамильтона градиент записывается так :
|
||
|
Теорема:
Поток векторного поля
Док-во:
Поток вектор.поля
an=a*n0=axcos+ aycos+ aycos=(ах,ау,az)(cosλ,cosμ,cosν)= тогда поток Q можно выразить так :
по формуле устанавливающей связь м/у интегралами 1 и 2 рода :
По формуле
Остроградского:
Заметим,
что под знаком тройного интеграла в
правой части стоит дивергенция
векторного поля
|
||
|
35. Производная по направлению. Связь ее с градиентом. Возьмем в поле скалярной величины некоторую ось l Возимем на ней 2 точки М(x,y,z) и N(x+x,y+y,z+z) Обозначим =прlMN ОПР Производной от U(x,y,z) по направлению l наз-ся
Заметим, что справа стоит скалярное призведение 2-х векторов:
проекция
максимальна, если
Всякая производная имеет смысл скорости. Наибольшая скорость изменения поля равна модулю grad и направление изменения скорости совпадает с направлением градиента |
||
|
40. Соленоидальное векторное поле. Свойства. Def:
Определение:
ее 2-мя поперечными сечениями. diva→=0. Пусть поле соленоидально, тогда поток Q=0 с другой стороны Q=Q1+Q2+Q3. Q3=0; Q=Q1+Q2. Q1=-Q1 Q1 и Q2 внешние нормали Q=-Q1- поток в противополжном направлении. Поток соленоидального вектор.поля через Поперечное
сечение вект.трубки сохраняет постоянное
значение и наз-ся напряжением векторной
трубки. Заметим, что если рассмотреть
поле V тек.жид.в которой нет источников
и истоков, то div ур-ие неразрывности. Таким соотношение связаны проекции скоростей текущей жидкости. |




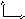







 24.
Криволинейные интегралы 1 рода,
определение, теорема существования.
Свойства.
24.
Криволинейные интегралы 1 рода,
определение, теорема существования.
Свойства.




 .
Продифиренцируем функцию Ф(x,y)
по переменной x.
Для этого, исходя из (.)
М(x,y),
дадим
x
приращение
x.,
взяв его столь малым, что отрезок MN,
соединяющий точки М(x,y)
и
N(x+x,
y),что
он целиком лежит а области S,
тогда :
.
Продифиренцируем функцию Ф(x,y)
по переменной x.
Для этого, исходя из (.)
М(x,y),
дадим
x
приращение
x.,
взяв его столь малым, что отрезок MN,
соединяющий точки М(x,y)
и
N(x+x,
y),что
он целиком лежит а области S,
тогда : ,
лишь бы только на этой кривой были бы
выполнениы условия т. сущ-я криволинейного
интеграла 2 рода.
,
лишь бы только на этой кривой были бы
выполнениы условия т. сущ-я криволинейного
интеграла 2 рода. .
С другой стороны интеграл по контуру
области Д .
.
С другой стороны интеграл по контуру
области Д .

 28.
Необходимое и достаточное условие
независимости криволинейного интеграла
от пути интегрирования.
28.
Необходимое и достаточное условие
независимости криволинейного интеграла
от пути интегрирования.

 36.
Векторное
поле, векторные линии, векторные
поверхности, векторная трубка.
36.
Векторное
поле, векторные линии, векторные
поверхности, векторная трубка.






 38.
Дивергениция векторного поля, ее
механический смысл.
38.
Дивергениция векторного поля, ее
механический смысл.
 39.
Векторная форма теоремы Гауса –
Остроградского.
39.
Векторная форма теоремы Гауса –
Остроградского.
