
- •1.Общая постановка задачи оптимизации. Локальный и глобальный экстремум.
- •3. Геометрический метод решения задач условной оптимизации(зуо)
- •5. Достаточные условия оптимальности в задаче безусловной оптимизации.
- •7. Обобщенное правило множителей Лагранжа в задаче с ограничениями типа равенств.
- •9. Необх. Условия оптимальности 2-го порядка в задаче условной оптимизации с огранич. Типа равенств.
- •11.Необх. Условия оптимальности 1-го порядка для гладких задач на условный минимум с огранич. Типа нер-в. Классич. И обобщённое правило множителей Лагранжа.
- •13. Достаточное условие локальной оптимальности для гладких задач на условный минимум с ограничениями типа неравенств.
- •15. Приведение задач линейного программирования (лп) к каноническому виду.
- •17. Критерий оптимальности базисного плана.
- •19. Итерация симплекс-метода.
- •21. Двухфазный симплекс-метод.
- •23. Связь между решениями прямой и двойственной злп.
- •25. Двойственная задача к тз. Методы построения нач. Пл. Достат. Условие оптим. Плана перевозок. Метод потенциалов решения транспортной задачи в матричной форме.
- •27. Выпуклые функции и их свойства. Унимодальные функции.
- •29. Необходимое условие оптимальности в задаче выпуклого программирования. Теорема Куна-Таккера.
- •31. Задача одномерной оптимизации. Метод деления отрезка пополам.
- •33. Задача одномерной оптимизации. Метод ломаных
- •35. Основные понятия численных методов безусловной оптимизации.
- •35. Основные понятия численных методов безусловной оптимизации.
- •37. Метод безусловного покоординатного спуска.
- •39. Метод условного градиетна.
- •43. Общая постановка задачи дп. Принцип оптимальности Беллмана.
- •45. Основная задача ви. Основные понятия.
- •47. Общее необх. Условие оптимальности для зви.
- •49. Усиленное усл. Лежандра. Ур-е Якоби. Усиленное усл. Якоби. Дост. Усл. Сильного минимума в осн. Зви.
- •51. Задача Больца.
31. Задача одномерной оптимизации. Метод деления отрезка пополам.
Задача одномерной минимизации имеет вид
 (1).
(1).
Метод деления отрезка пополам основывается на понятии унимодальной ф-ции.
Опр.1 Непрерывную функцию наз. унимодальной, если , что слева от нее функция убывает, а справа от неё возрастает, т.е. :

- на рисунке унимодальная ф-ция
Опр.2 Непрерывную функцию наз. строго унимодальной, если , что :
Т.о. у строго унимодальной функции может быть только одна точка, у нестрого унимодальной – целые отрезки.
Далее будем строить методы, кот. позволяют найти одну точку минимума для любой унимодальной ф-ции.
В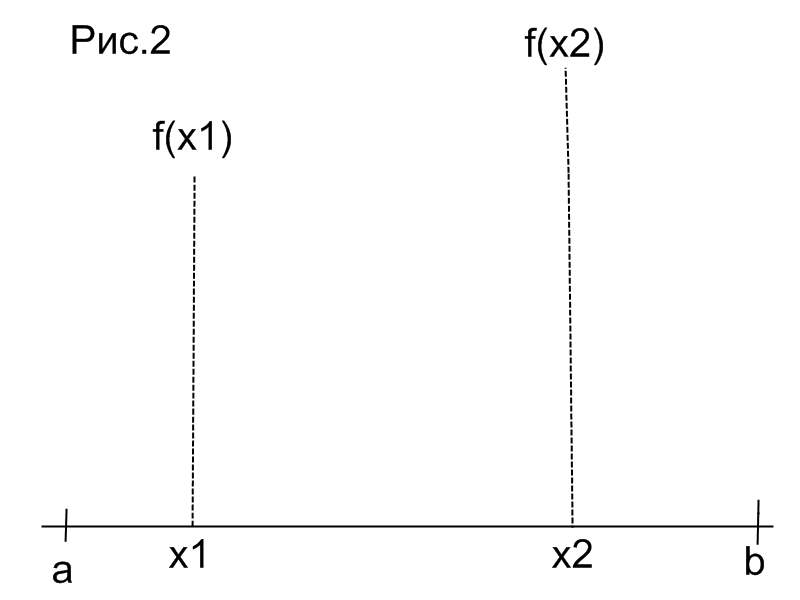 озьмем
любые две точки
озьмем
любые две точки


 .
Тогда в силу унимодальности функции
.
Тогда в силу унимодальности функции
 на отрезке
на отрезке
 функция не может достигать своего
минимума, тогда отрезок поиска сужается
до отрезка
функция не может достигать своего
минимума, тогда отрезок поиска сужается
до отрезка
 .
(Рис.2)
.
(Рис.2) ,
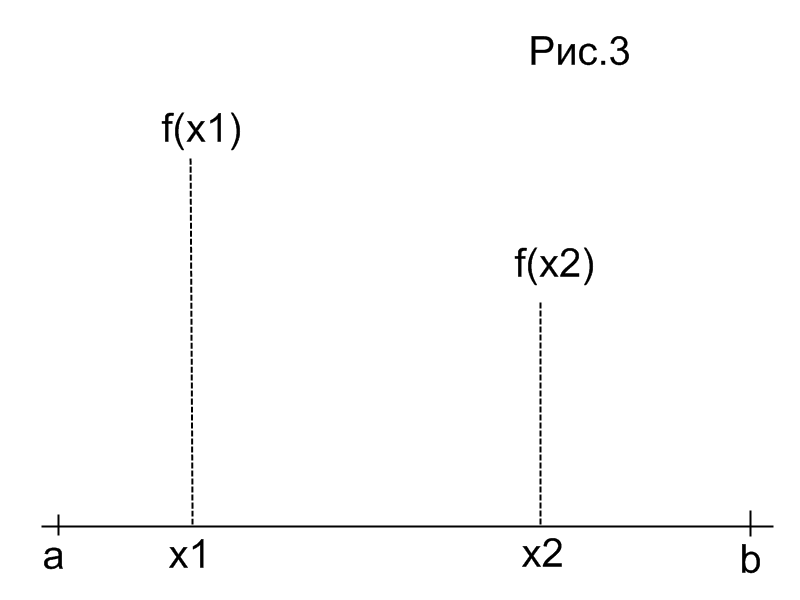
то отрезок поиска
,
то отрезок поиска
сужается
до отрезка
 (Рис.3)
(Рис.3)

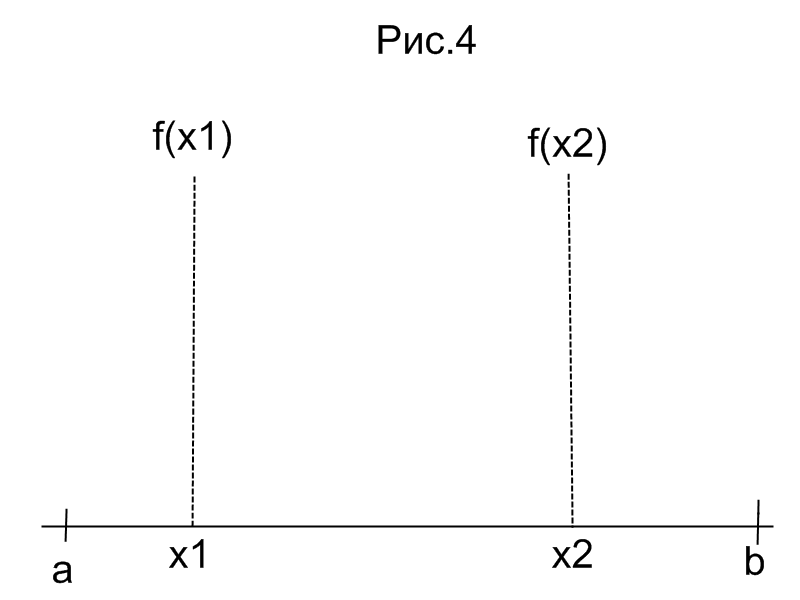 .
Отрезок поиска сужается до отрезка
.
Отрезок поиска сужается до отрезка
 .
(Рис.4)
.
(Рис.4)
Такую
идею поиска точки минимума использует
2 метода: метод деления отрезка пополам
и метод «золотого сечения». Они отличаются
только способами выбора точек
 и
и
 .
.
Алгоритм метода деления отрезка пополам.
Выбираем параметры метода
 .
.Вычисляем пробные точки
 .
.Вычисляем значения целевой функции в точках
 .
.
Если
 ,
то
,
то
 ;
;
если
 ,
то
,
то
 ;
;
если
 ,
то
,
то

Если выполняется условие остановки
 ,
то точка минимума
,
то точка минимума
 с точностью
с точностью
 .
.Если условие остановки не выполняется, то k=k+1 и переходим на шаг 2.
33. Задача одномерной оптимизации. Метод ломаных
Задача одномерной минимизации имеет вид
(1).
Метод применяется для задачи (1) при условии, что f(x) удовлетворяет условию Липшица.
Опр.
Говорят, что функция f(x)
,
 удовлетворяет
условию Липшица с константой L,
если нер-во
удовлетворяет
условию Липшица с константой L,
если нер-во
 ,
,

Метод
состоит в последовательной аппроксимации
снизу ф-ции f(x)
кусочно-линейными ф-циями
 Рассмотрим ф-цию
Рассмотрим ф-цию
 . Точка
. Точка
 определяет два луча, симметричных
относительно прямой, проходящей через
определяет два луча, симметричных
относительно прямой, проходящей через
 и перпендикулярной отрезку
и перпендикулярной отрезку
 .
.
Алгоритм метода ломанных:
Задаем параметры метода
 причем
причем

Выбираем начальную точку
 (либо правый, либо левый конец отрезка
)
(либо правый, либо левый конец отрезка
)Строим ломанную

Строим общую ломанную, т.е. кусочно-непрер. ф-цию

Точку
 ищем как решение задачи
ищем как решение задачи
 (другая
запись)
(другая
запись)Проверяем условие остановки
 Если
оно выполняется, то
Если
оно выполняется, то
 - точка минимума с точностью
- точка минимума с точностью
 ,
иначе k=k+1
и переход на шаг 3. Покажем, что функция
,
иначе k=k+1
и переход на шаг 3. Покажем, что функция
 апроксимирует ф-цию f(x)
всегда снизу. Для этого достаточно
показать, что
апроксимирует ф-цию f(x)
всегда снизу. Для этого достаточно
показать, что
 .
.
Т.к.
 то
по опред. ф-ции
то
по опред. ф-ции
 имеем
имеем

Как найти L? Для нахождения константы Липшица можно воспользоваться утверждением.
Утв1.
Пусть функция f(x)
дифференцируема и
 ограничена. Тогда
ограничена. Тогда
 удовлетворяет усл. Липшица с константой
удовлетворяет усл. Липшица с константой

Пример.



