13. Достаточное условие локальной оптимальности для гладких задач на условный минимум с ограничениями типа неравенств.

Рассмотрим задачу условной оптимизации с ограничениями типа неравенств

(1)

Пусть , i=1, …,m

Определение. Точка называется условно стационарной точкой задачи (1), если существует -вектор такой, что выполняются условия

Теорема. (дост. усл. лок. оптимальности задачи (1)). Для локальной оптимальности условно стационарной точки задачи (1) достаточно, чтобы квадратичная форма была положительно определена для всех векторов таких, что

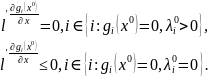
15. Приведение задач линейного программирования (лп) к каноническому виду.

1. Если

2. Пусть задача линейного программирования записана в нормальной форме

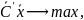
, где

, .

3. .

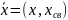Введем обозначения это элементы вектора x, причем 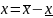и введем , где .

Тогда исходная задача увеличится в количестве неизвестных переменных в 2 раза и примет вид

, . .

Упражнение. Привести к каноническому виду задачи л.п.

1. 

Эту задачу можно переписать в виде

, тогда - основные ограничения, а 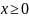– прямое ограничение.

2. 

Эту задачу можно свести к предыдущему пункту заменой , а именно

3. 

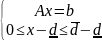
Эту задачу можно переписать в след. виде

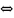
Введём вектор свободных переменных . Тогда новый вектор , а , .

17. Критерий оптимальности базисного плана.

Теорема. Для оптимальности базисного плана достаточно, а в случае невырожденности и необходимо, чтобы оценки .

Доказательство. Достаточность. Дано . Воспользуемся также формулой построения плана , т.е. Рассмотрим только небазисные компоненты , учитывая что , имеем оценку

Учитывая формулу , имеем

, т.к. Значит,

- оптимальный базисный план (значение целевой функции на плане не превышает значение целевой функции на плане ).

Необходимость. Пусть - оптимальный невырожденный базисный план, т.е. , ( ).

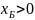Доказательство проведём от противного. Допустим, что номер , что . Построим план , кот. получается при переходе от плана с учетом след. Изменений

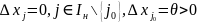
Тогда (не будет изменений в небазисных компонентах, кроме элемента с номером ).

(чтобы выполнялось ).

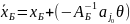
– должен быть планом задачи , значит должны выполняться прямые ограничения. Напомним, что Тогда, если

1. то , т.к. 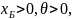что означает положительную определенность .

2. 

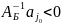
1. то предположение о невырожденности x необходимо для того, чтобы

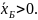
2. то можно сделать максимально возможный шаг такой, что

Т.о. показали, что построенный вектор является планом.

_{Рассмотрим приращение целевой функции при переходе от плана} к плану _.

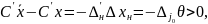т.к. Значит, - противоречие оптим. базового плана x.

_Значит не существует , что 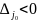, т.е.