1.Общая постановка задачи оптимизации. Локальный и глобальный экстремум.

Пусть ф-ция f(x) задана на некот. мн-ве Х-мн-во любой природы. Задача оптимизации состоит в нахождении минимума или максимума ф-ции f(x) на мн-ве X. Математическая это записывается так

f(x) extr, x , (1)

Задача (1) подразделяется на две:

1. задача минимизации f(x) min, x (2)

2. задача максимизации f(x) max, x (3)

(сводится к задаче минимизации, если рассматривать ф-цию )

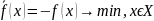Различают локальный и глобальный минимум.

Опр1. Точка наз. точкой локального минимума задачи (2), если , что для выполняется неравенство

Опр2. Точка наз. точкой глобального минимума задачи (2), если неравенство выполняется

Глобальное решение является локальным, обратное верно не всегда

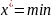-лок.мин.

Опр. Точка x в задаче (2) наз. планом. Если x , то х наз. допустимой точкой или допустимым планом.

Ф-ция f(x) наз. целевой ф-цией или критерием качества.

Опр. Решения задач (2) и (3), т.е. точки минимума и точки максимума ф-ции f(x) наз. точками экстремума, а сами задачи (2) и (3) экстремальными задачами.

3. Геометрический метод решения задач условной оптимизации(зуо)

Задача наз. ЗУО. ЗУО можно решить графическим методом, если 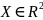и вид мн-ва Х описывается дост. простыми неравенства, в частности системой линейных неравенств. Решение строится на понятии линии уровня.

Опр. Линией уровня функции наз. множество вида

Придавая параметру различные значения получим различные линии уровня ф-ции f(x).

ЗУО, кот. можно решить графически

. (1)

Схема решения:

1. В плоскости cтроим множество

Если 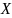построить невозможно, то задача (1) не имеет решения.

2. Строят несколько линий уровня ф-ции f(x).

3. По линиям уровня определяем направление возрастания или убывания целевой функции (направление grad определяет направление возрастания функции).

4. Двигаясь по линиям уровня в направлении убывания до тех пор, пока линия уровня последний раз коснется мн-ва Х находим точку минимума, аналогично находят точку максимума.

Замечание! В задаче (1) может отсутствовать точка минимума или максимума, когда множество Х неогр.

5. Достаточные условия оптимальности в задаче безусловной оптимизации.

Теорема (дост. условия локальной оптимальности).

Пусть f Для того, чтобы стационарная точка - была точкой лок. минимума задачи , достаточно чтобы матрица её вторых производных была положительно определена ( ). (1)

Док-во. (от противного)

Пусть условие (1) выполняется точка - стационарная, но не явл. точкой лок. минимума. Построим последовательность точек по закону

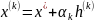, где .

Из разложения в ряд Тейлора следует:

Учитывая, что имеем

Делим на , устремим

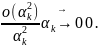
Получили противоречие!!!