Истечение при переменном уровне жидкости в сосуде с целью определения времени опорожнения сосудов

При таком истечении жидкости (рис. 6.6б) ее уровень Н в сосуде снижается во времени и, согласно уравнению (6-9), уменьшается также скорость истечения . Следовательно, процесс истечения носит нестационарный характер.

Определим время, за которое уровень жидкости в сосуде опустится от первоначальной высоты до некоторой высоты . За бесконечно малый промежуток времени , в соответствии с уравнением (6-10), через отверстие в днище вытечет объем жидкости

,

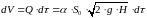где – площадь поперечного сечения отверстия в днище сосуда.

За тот же промежуток времени уровень жидкости в сосуде понизится на бесконечно малую величину 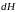, и при постоянной площади поперечного сечения сосуда убыль жидкости в нем составит

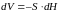
Знак минус в правой части указывает на уменьшение высоты жидкости в сосуде.

Приравнивая, согласно уравнению неразрывности потока, эти объемы, получим

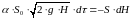
Откуда

Проинтегрируем это выражение, принимая, что коэффициент расхода постоянен, т.е. не зависит от скорости истечения:

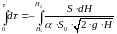
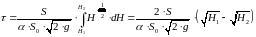
Таким образом, время опорожнения сосуда, имеющего постоянное поперечное сечение, от высоты до высоты составляет

6-12

В случае полного опорожнения резервуара и уравнение (6-12) принимает вид

6-12а

Лекция 7

7.1 Понятие о моделировании процессов

Пути исследования процессов химической технологии. Сущность теории подобия и моделирования процессов. Изучение процессов с целью получения уравнений, необходимых для их анализа и расчета, можно проводить чисто теоретически. Этот наиболее желательный путь исследования сводится к составлению (на основе самых общих законов физики и химии) и решению математических зависимостей, чаще всего дифференциальных уравнений, полностью описывающих процесс.

Примером важных для практики расчетных зависимостей, полученных решением соответствующих дифференциальных уравнений, являются рассмотренные выше основное уравнение гидростатики и уравнение Бернулли.

Дифференциальные уравнения описывают целый класс однородных по своей сущности явлений, и для выделения из него конкретного явления необходимо ограничивать указанные уравнения дополнительными условиями (условиями однозначности).

Условия однозначности включают: геометрические форму и размеры системы, т. е. аппаратуры, в которой протекает процесс; существенные для данного процесса физические константы участвующих в нем веществ; начальные условия, к числу которых относятся начальная скорость, начальная температура, начальная - концентрация и т. п.; граничные условия, характеризующие состояние на границах системы, например равенство нулю скорости жидкости у стенок трубы, и т. д.

Таким образом, дифференциальные уравнения должны решаться в совокупности с условиями однозначности в устанавливаемых последними пределах.

Однако многие процессы химической технологии характеризуются большим числом переменных и настолько сложны, что зачастую удается дать лишь математическую формулировку задачи и установить условия однозначности. Полученные же дифференциальные уравнения не могут быть решены известными в математике методами.

Иллюстрацией этому являются уравнения Навье–Стокса, решение которых оказывается невозможным для большинства важнейших практических случаев, в частности для определения теоретическим путем потерь напора (гидравлического-сопротивления) при турбулентном движении.

С аналогичными трудностями приходится сталкиваться при теоретических исследованиях процессов тепло- и массообмена в турбулентных потоках, а также процессов, протекающих в реакционных аппаратах, в которых химические превращения осложнены движением потоков и тепло- и массопередачей. Более того, для очень сложных процессов даже нельзя составить систему дифференциальных уравнений, исчерпывающе описывающих данный процесс.

Таким образом, теоретический вывод расчетных зависимостей, необходимых для проектирования аппаратуры, часто оказывается невозможным. В таких случаях для нахождения связи между величинами, характеризующими процесс, прибегают к экспериментальному исследованию, т. е. к проведению опытов.

На основе опытных данных часто получают эмпирические уравнения, которые являются частными и не могут быть распространены на условия, отличные от тех, для которых они получены. Эти частные эмпирические уравнения имеют известную ценность и используются в инженерной практике.

Однако наиболее плодотворно такое осуществление экспериментов, которое позволяет обобщать результаты опытов и распространять их на широкий круг явлений, подобных изученному, но отличающихся численными значениями характерных параметров, например размеров аппарата, основных физических свойств среды и т. д. Это достигается при использовании для обработки опытных данных методов теории подобия.

Теория подобия является учением о методах научного обобщения эксперимента. Она указывает, как надо ставить опыты и как обрабатывать их результаты, чтобы при проведении небольшого числа экспериментов иметь возможность обобщать опытные данные, получая единые уравнения для всех подобных явлений. Применение теории подобия часто позволяет вместо дорогостоящих трудоемких опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера; помимо этого, опыты можно проводить не с рабочими (часто вредными и опасными) веществами и не в жестких (высокие температуры, сильно агрессивные среды) условиях реального производственного процесса, а с другими (модельными) веществами в условиях, отличающихся от промышленных.

Проведение опытов на моделях, по меткому выражению Бэкеланда, позволяет делать ошибки в малом масштабе, а выгоды получать в большом.

Таким образом, методы теории подобия лежат в основе масштабирования и моделирования процессов.

В широком смысле под моделированием понимают метод исследования, при котором вместо непосредственно интересующего нас процесса или явления, протекающего в каком-то объекте (натуре), изучается соответствующий процесс на другом объекте (модели).

Следует отметить, что в литературе под термином «модель» не всегда понимают материальную модель, на которой проводятся исследования. Часто моделью считают некоторую познавательную, или мысленную, физическую или математическую модель, т. е. схему, с той или иной степенью точности отражающую наиболее существенные стороны изучаемого процесса. Такие модели, которые в отличие от материальных можно также назвать идеальными, кладут в основу исследования данного процесса или явления. Примерами могут служить модели структуры потоков в аппаратах, модели массопередачи и др., рассматриваемые в настоящем курсе. На основе принятой идеальной физической модели составляют соответствующую ей математическую модель, т. е. математическое описание процесса.

Вместе с тем методы теории подобия часто применяются и при использовании других видов моделирования, в которых моделирующие процессы отличаются от моделируемых по физической природе. Важнейшим из них является математическое моделирование, при котором различные процессы воспроизводятся на электрических моделях – электронных вычислительных машинах.

Прогрессивное значение теории подобия и моделирования, позволяющей быстрее и экономичнее исследовать процессы и с достаточной степенью надежности переходить от лабораторных масштабов к производственным, сохраняя при этом интенсивность и другие оптимальные показатели данного процесса, по достоинству оценено в ряде отраслей техники, где теория подобия нашла широкое применение (котлостроение, кораблестроение, самолетостроение, строительство гидростанций и т. д.). В химической технологии обобщение экспериментальных данных методами теории подобия внесло большой вклад в изучение закономерностей процессов гидравлики, тепло- и массопередачи.

Однако, используя методы теории подобия, указывающие рациональные пути постановки опытов и обработки полученных экспериментальных данных для вывода обобщенных расчетных зависимостей, надо иметь в виду, что теория подобия не может дать больше того, что содержится в исходных уравнениях, описывающих исследуемый процесс. Она лишь позволяет посредством обобщения результатов опытов найти интегральные решения этих уравнений, действительные для группы подобных явлений в исследованных пределах, без проведения собственно интегрирования. Если исходные уравнения неверно описывают физическую сущность процесса, то и конечные-результаты, полученные при использовании методов теории подобия, будут неправильными.