Распределение скоростей и расход жидкости при установившемся ламинарном потоке

В случае ламинарного движения вязкой жидкости в прямой трубе круглого сечения всю жидкость можно мысленно разбить на ряд кольцевых слоев, соосных'с трубой (рис. 2).

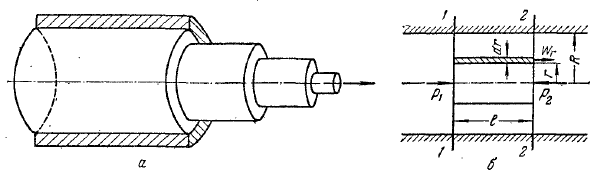
Рис. 2 К определению распределения скоростей и расхода жидкости при ламинарном движении.

Вследствие действия между слоями сил трения слои будут двигаться с неодинаковыми скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную скорость, но, по мере удаления от оси, скорость элементарных кольцевых слоев будет уменьшаться. Непосредственно у стенки жидкость как бы «прилипает» к стенке, и ее скорость здесь обращается в нуль.

Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R (рис. 2, б), цилиндрический слой длиной l и радиусом r.

Движение слоя происходит под действием разности сил давления P₁ и Р₂ с обеих торцовых сторон цилиндра:

где – гидростатические давления в сечениях 1–1 и 2–2.

Движению цилиндра оказывает сопротивление сила внутреннего трения Т, для которой, справедливо выражение

где – скорость движения жидкости вдоль оси цилиндра ьа расстоянии г от оси;

– наружная поверхность цилиндра;

– вязкость жидкости.

Знак минус указывает на убывание скорости с увеличением радиуса r (при r = R величина w_r = 0).

При установившемся движении разность сил давления затрачивается на преодоление силы трения T, и сумма проекций всех этих сил на ось потока должна быть равна нулю. Вследствие трения движение рассматриваемого цилиндрического слоя тормозится, значит, сила трения, приложенная к его боковой поверхности, направлена противоположно разности и проектируется на ось, направление которой совпадает с направлением движения, со знаком минус. Следовательно

или

откуда, после сокращения и разделения переменных, получим

Переходя ко всему объему жидкости в трубе, проинтегрируем это дифференциальное уравнение, учитывая, что радиус в левой части уравнения изменяется от до , а переменная скорость в правой части – от w = w_r до w 0 0 (у стенки, где )

Тогда

или

4-5

Скорость имеет максимальное значение на оси трубы, где :

4-5a

Сопоставляя выражения (4-5) и (4-5a), находим

4-6

Уравнение (4.6) представляет собой закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении.

Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение (рис. 2, б) с внутренним радиусом и внешним радиусом , площадь которого равна . Объемный расход жидкости через это сечение составляет

или с учетом уравнения (4-5)

Интегрируя последнее уравнение, получим общий расход жидкости через трубу:

4-7

Подставляя вместо диаметр трубы и обозначая , окончательно находим

4-7а

Уравнение (4-7) или (4-7а), определяющее расход жидкости при ее ламинарном движении по круглой прямой трубе, носит название уравнения Пуазейля.

Соотношение между средней скоростью и максимальной скоростью можно получить, сопоставив значение Q из уравнений (4-1) и (4-7):

откуда

4-8

Сравнивая уравнения (4-5а) и (4-8), находим

4-9

Таким образом, при ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы.

Соответственно параболический закон распределения скоростей по сечению трубы, выражаемый уравнением (4-6), может быть представлен в виде

4-6а

Этот закон, выведенный теоретически, хорошо подтверждается эпюрами скоростей, полученными опытным путем (рис. 3, а).

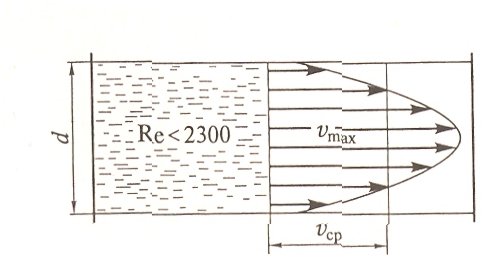
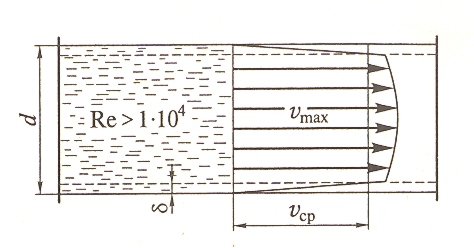
Рис. 3. Распределение скоростей при различных режимах движения: a - ламинарный поток; б – турбулентный поток.