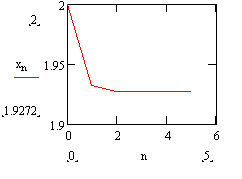
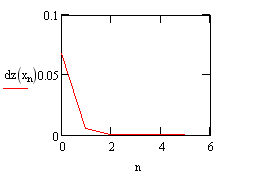
2. Метод хорд

Задание 2. Решить уравнение = 0 методом хорд с точностью  =10^-3

1.Отделение корней (см. п. 1.1).

2.После того как корень, подлежащий уточнению, отделен, за начальное приближение может быть выбрана лю­бая точка отрезка (начало, его середина и т. д.).

3.Уточнение значений корней и проверка критерия достижения заданной точности. Найдите первую производную функции f(x). Постройте последовательность значений с использованием рекуррентной формулы метода хорд и проанализируйте результаты вычисленных значе­ний последовательности х_n. Для этого следует рассмотреть значения функции dz(x_n) - эта величина является критерием достижения задан­ной точности  = 0,001. Начиная с п = , значения х_п удовлетворяют критерию достижения заданной точности ( > ), значит, x_n = - решение данного уравнения.

4.Создание функции, реализующей вычисления корня уравнения

= 0 на отрезке [ ] с точностью e = 0,001 методе хорд (рис.3). Решением будет являться число x_n = , получившееся на шаге решения.

Рис.3. Проверка критерия достижения заданной точности и использование встроенной функции, реализующая метод хорд (файл fhord.mcd).

Ответ: корень уравнения по методу хорд равен с точностью 0,001, най­денный на 2

шаге.

3. Метод касательных Задание 3. Вычислить методом касательных корень уравнения = 0 на отрезке [ ] с точностью e = 0,001.

1. Отделение корней. Отделите корни уравнения (см. п. 1.1).

2. Определение неподвижной точки. Для этого определите знаки функции и второй производной на отделенном интервале [ ] и определяем неподвижную точку, сравнивая

знаки функции и второй производной . Для этого составьте функцию, проверяющую условие неподвижности точки

Рис. 4. Определение неподвижной точки (файл nt.mcd).

В точке х = знаки функции и второй производной совпадают, значит, она будет неподвижной точкой. Тогда подвижной точкой будет точка a = 1.5, которую можно взять в качестве начального приближения х₀

3. Задаем число шагов и начальное приближение: 4.Записываем рекуррентную формулу метода касательных и вычисляем полученные значения итерационной последовательности с использованием этой формулы

5. Определим критерий достижения заданной точности при решении уравнения методом касательных и сравним его со значением ε = 0.001

Рис. 5. Построение итерационной последовательности по методу касательных

Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что число в последовательности < 0,001. Значит, решением уравнения будет значение х_n = при n = .

6. Проанализируем полученные результаты, построив несколько графиков:

а)	б)	в)

Рис. 6. Зависимости: а) значения корня от шага итерации, б) значения функции от шага итерации, в) погрешности от шага итерации (n).

Из графиков видно, что решение получается на -ом шаге итерационного процесса. Это подтверждается и полученными значениями по формулам (аналитически).

7. Создание функции, реализующую метод касательных.

Рис. 7. Использование встроенной функции, реализующая метод касательных (файл kasat.mcd)

Ответ: Значит, корнем уравнения будет число x = , которое получается на - ом шаге.

Графические возможности пакета позволили подробно исследовать процесс решения уравнения методом касательных.

4. Метод простой итерации Задание 4.Решить уравнение = 0 методом простой итерации с точно­стью e = 0,001. Схема решения уравнения методом простой итерации следующая.

1.Отделение корней. Отделите корни уравнения (см. п. 1.1). 2. Приведение исходного уравнения к каноническому виду х = f (x). Для этого замените уравнение е^х •(2-х)-0,5 = 0 уравнением вида x-x-m•F(x). Здесь величина m должна быть подобрана так, чтобы для функции f(х) выполнились условия 2 и 3 теоремы о достаточном условии сходи­мости итерационного процесса. Производная F'(x) на отрезке [ ] отрицательна, следовательно, функция F(x) на этом отрезке монотонно убывает.

Рис. 8. Определение значения m и критерия достижения заданной точности q.

3. Определение значения m и критерия достижения заданной точности q (рис 8). Поскольку производная F'(x) на концах интервала [ ] отрицательна и монотонно убывает, ее мо­дуль имеет максимум на правом конце отрезка. Тогда за m можно принять значение m = - 0.055, а за q = 0. 877.

4. Вычисление значений итерационной последовательности х_п. В качестве начального значения можно взять, например, начало отрезка, точку х₀ = . Критерием достижения заданной точности e = 0,001 при решении данного уравнения методом простой итерации является величина , paвная. Для -го приближения получили, что < A. Отсю­да следует, что x = является приближенным решением этого уравнения.

5. Создание функции, реализующую метод простой итерации для решения уравнения

x = f(x) по методу простой итерации (Рис. 9. )

Рис. 9. Проверка критерия достижения заданной точности и использование встроенной функции, реализующая метод простой итерации (файл Iter.mcd).

6.Визуализация решение уравнения методом простой итерации

а)

б)

в)

Рис. 10. Зависимости: а) значения корня от шага итерации, б) значения функции от шага итерации, в) погрешности от шага итерации (j).

Ответ: решением уравнения будет число х = , полученное на -м шаге.

Задание 5. Проверка решения задачи встроенными возможностями пакета Mathcad

Рис. 11. Проверка решения уравнения встроенными функциями Mathcad

Задание 6. Согласно номеру предложенных вариантов (табл. 2.2.1, стр. 232 -233) отделите корни уравнения графически и уточните один с точностью e = 0,001 из них методом хорд и касательных (задача 1), методами половинного деления и простой итерации (задача 2) . Создать функции, реализующие указанные методы, построить графическую иллюстрацию методов, результаты проверить с помощью встроенных функций Mathcad, оценить точность полученных значений.

экспериментальная ч асть

работы выполнена _________________20 г. /подпись / _______________ Работа защищена_____________20 г. Преподаватель / подпись/ _________________