Лабораторная работа № 1 Численные методы решения скалярных уравнений

Ф.И.О. студента Неелова Ж.В. гр. № 1Ф-210 Институт ИИТ

Цель работы: сформировать:

• представление о применении уравнений в различных областях научной деятельности; знания об основных этапах решения уравнения;

• дать навыки в использовании программных средств для составления и применения алгоритмов численного решения уравнений на основе прямых и итерационных методов;

• навыки в выборе того или иного программного средства для уточнения корней уравнений и проверки правильности найденного результата.

Вопросы при допуске к работе

1. Что значит численно решить уравнение ?

Численное решение уравнений  состоит в приближённом определении корня или корней уравнения и применяется в случаях, когда точное значение вычислить невозможно или очень трудоёмко.

2. Какие существуют методы решения уравнения с одной неизвестной (с п неизвестными)?

3. Какие методы решения уравнения с одной неизвестной относятся к прямым и приближенным методам

решения?

4. Каковы этапы решения уравнения с одной неизвестной численными методами?

5. В чем заключается этап отделения корней при использовании численных методов решения уравнения?

6. В чем заключается метод половинного деления? Найдите файлы Div2.mcd, Div2I.mcd

1.2.3. Метод половинного деления

Пусть уравнение (1.2.1) имеет на отрезке [а, b] единственный корень, причем функция F(x) на данном отрезке непрерывна (рис. 1.2.1).

Разделим отрезок [а,b] пополам точкой Если , то возмож­ны два случая:

• функция F(х) меняет знак на отрезке [а, с],

• функция F(x) меняет знак на отрезке [с, b].

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и, продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

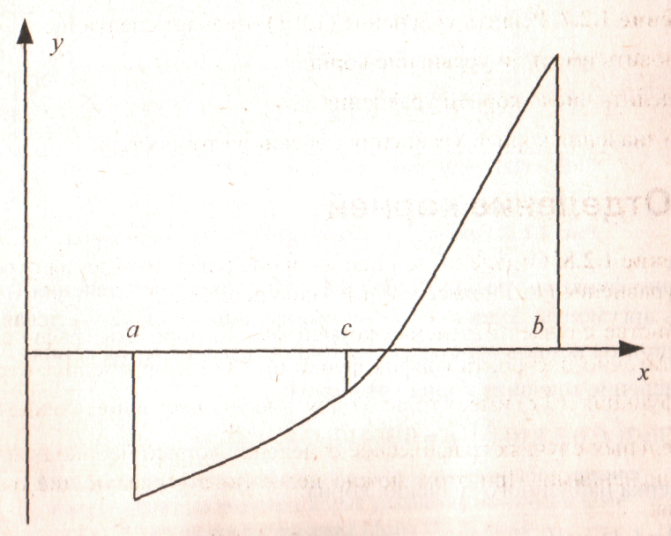
РИС. 1.2.1. к объяснению метода половинного деления

Пример 1.2.1.

Решение в пакете Mathcad методом половинного деления уравнения

1. Задание функции:

2. Построение графика функции (рис. 1.2.2).

Рис. 1 .2.2. График функции

3. Задание функции, реализующей метод половинного деления (рис. 1.2.3). Здесь аргументы функции: f - имя функции, х1, х2 — левая и правая координаты концов отрезка; ε — точность вычисления корня.

4. Вычисление значения корня уравнения:

5. Проверка найденного значения корня:

Для рассмотрения процесса нахождения корня уравнения в динамике необходимо сохранить значение корня на каждом шаге вычислительной процедуры и построить зависимость значении корня от номера шага. Функция, возвращающая значение корня на каждом шаге метода поло­винного деления, представлена на рис. 1.2.4. Аргументы функции: f — имя функции, х1, х2 — левая и правая координаты концов отрезка, ε — точность вычисления корня

Рис. 1.2.3. Функция, реализующая метод половинного

деления (файл Div2.mcd)

Рис. 1.2.4. Функция, реализующая метод половинного деления

и возвращающая значение корня уравнения на каждом шаге

процесса вычислений (файл Div2I.mcd)

После создания функции необходимо дополнить описанный выше документ следующей последовательностью команд.

1. Вычисление матрицы, первый столбец которой содержит номер итерации, второй — значение корня:

2. Визуализация зависимости значения корня от номера шага вычислительной процедуры (рис. 1.2.5).

Рис. 1.2.5. Зависимость значения корня от номера шага

вычислительной процедуры

7. Сформулируйте основы метода хорд и дайте его графическую интерпретацию. Найдите файл fhord.mcd

9. Выведите формулу нахождения значений последовательности при реше­нии уравнения методом хорд.

8. Какое условие является критерием достижения заданной точности при решении уравнения х = f(x) мето-

дом хорд?

10. Сформулируйте основы метода касательных и дайте его графическую интерпретацию. Найдите файлы

nt.mcd, kasat.mcd

11. Выведите формулу нахождения значений последовательности при реше­нии уравнения методом касатель-

ных.

12. Какое условие является критерием достижения заданной точности при решении уравнения х = f(x) мето-

дом касательных?

13. Сформулируйте основы метода простой итерации для решения уравнений? Найдите файл Iter.mcd

14. Какие уравнение можно решать методом простой итерации? Что такое сжимающее отображение?

15. Как строится итерационная последовательность точек при решении уравнения методом простой итерации

16. Каковы достаточные условия сходимости итерационного процесса при решении уравнения х = f(x) на от

резке [a, b], содержащего корень, методом простой итерации?

17. Какое условие является критерием достижения заданной точности при решении уравнения х = f(x) мето-

дом итераций?

18. Как привести исходное уравнение к каноническому виду х = f (x) и определить критерий достижения задан

ной точности q ?

19. Назовите встроенными функциями Mathcad для численного решения уравнения