Метод наименьшей стоимости (мнс) или метод наименьших затрат.
Суть метода заключается в том, что на каждом этапе в таблице поставок в первую очередь заполняем клетку с наименьшей стоимостью.
Пример. Найти методом наименьшей стоимости первоначальное распределение поставок в ТЗ, заданной таблицей 4.
Решение. Находим в таблице поставок клетку с наименьшей стоимостью. Это клетка (2,2). Полагаем x2 2=min(80,80)=80. При этом эказывается в ситуации, когда потребности второго потребителя полностью удовлетворены, и запасы второго поставщика полностью исчерпаны. Можно исключить из рассмотрения только один ряд таблицы перевозок, например, второй столбец. При этом считаем, что запасы второго поставщика равны нулю. В оставшейся таблице снова находим клетку с наименьшей стоимостью. Это клетки (2,1) и (2,3). Так как запасы второго поставщика равны нулю, то отправляем нулевой груз в любую ищ этих клеток, например, в (2,3), её заштриховываем и считаем базисной. Вторую строку таблицы перевозок исключаем из рассмотрения. В оставшейся таблиц снова находим клетку с наименьшей стоимостью и так далее. Построенное исходное допустимое базисное решение представлено в таблице 6.
Пункт отправления |
Пункт назначения |
B1 |
B2 |
B3 |
B4 |
запасы |
A1 |
5
|
2
|
5 20 |
6 40 |
60 |
|
A2 |
3 |
1 80 |
3 0 |
7
|
80 |
|
A3 |
4 40 |
5 |
4 30 |
6
|
70 |
|
потребности |
40 |
80 |
50 |
40 |
210 |
|
Таблица 6
Ответ:
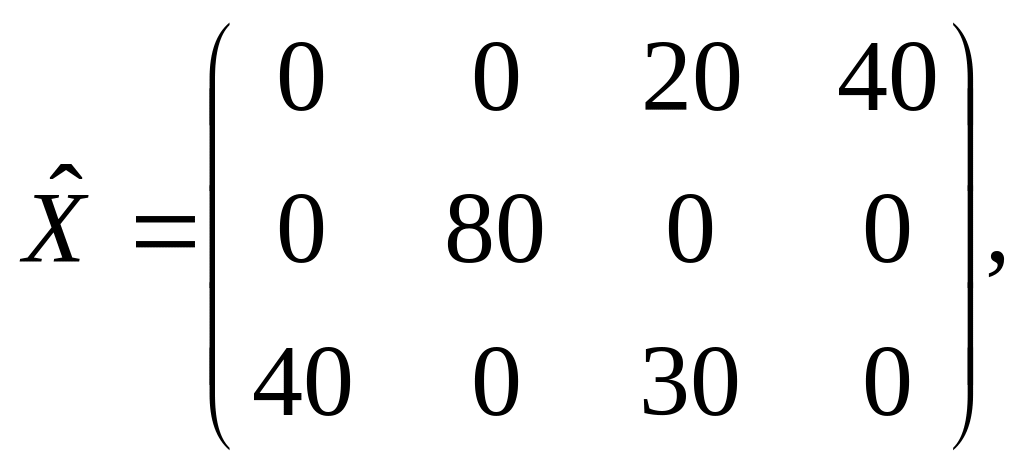
f0=5*20+6*40+1*80+3*0+4*40+4*30=700.
Число заполненных клеток оказалось равным 6, т.е. числу базисных переменных m+n-1.
Так как метод наименьшей сложности учитывает коэффициенты затрат задачи, то исходное распределение поставок, как правило, ближе к оптимальному, чем по методу северо-западного угла.
Следующий этап решения – определить, является ли построенное решение оптимальным.
4.3. Циклы таблицы перевозок и их свойства.
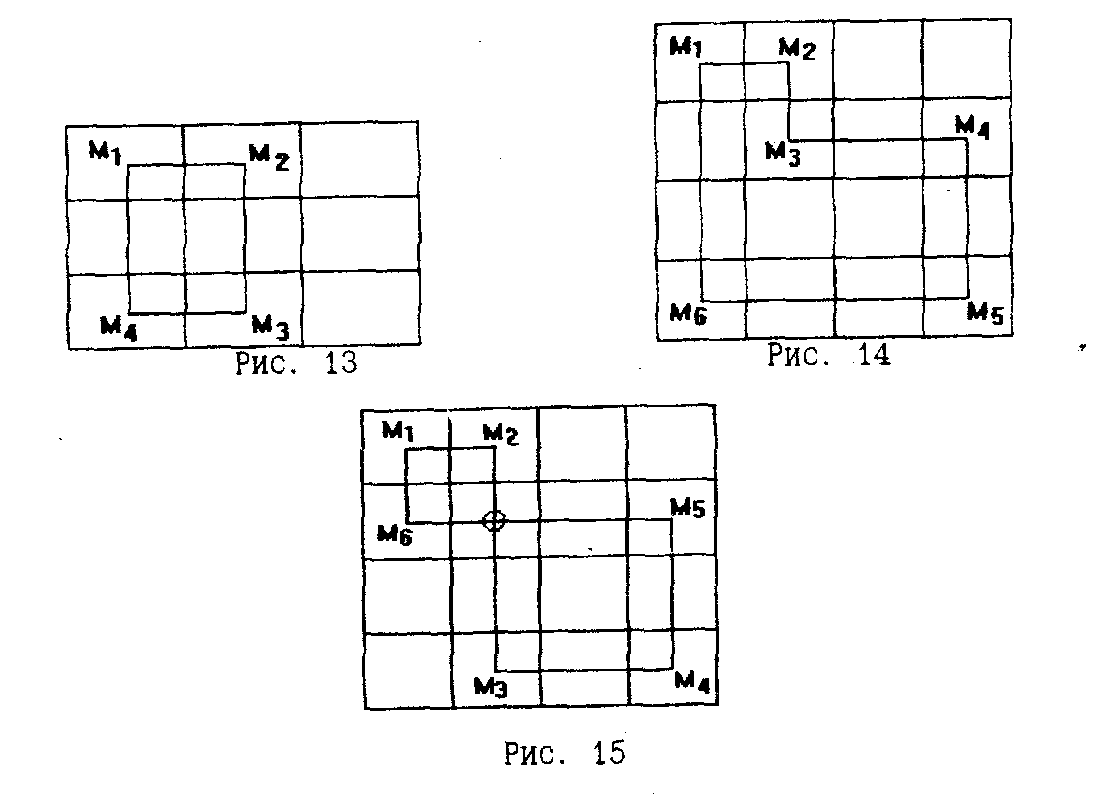
Определение. Циклом таблицы перевозок называется замкнутая ломаная линия, вершины которой находятся в клетках таблицы перевозок, а звенья расположены вдоль строк и столбцов таблицы. Причём в каждой вершине встречаются ровно два звена, одно из которых расположено по строке, другое – по столбцу таблицы (рис. 13, 14, 15).
Замечание. Цикл может иметь точки самопересечения, которые не являются вершинами (рис. 15).
Определение. Две вершины, являющиеся концами одного звена называются соседними.
Определение. Цикл назовём означенным, если каждой его вершине приписан знак «+» или «-», причём так, что знаки чередуются (рис. 16).
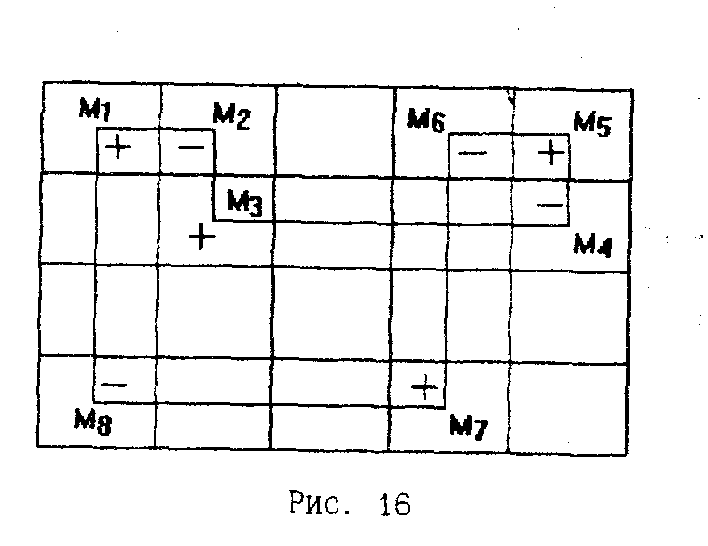
Свойства циклов таблицы перевозок:
Никакие три последовательные вершины цикла таблицы перевозок не могут находиться в одной строке (столбце).
Число вершин цикла перевозок чётно.
В каждой строке (столбце) таблицы перевозок число положительных вершин означенного цикла равно числу отрицательных вершин.
Пусть известно исходное допустимое базисное решение, построенное методом СЗУ или МНС, и в таблице перевозок взят некий означенный цикл.
Определение. Операцией сдвиг по циклу на число назовём увеличение всех значений xij, стоящих в положительных вершинах цикла на некоторое число , и уменьшения на то же число тех значений xij, которые стоят в отрицательных вершинах означенного цикла.
Теорема (о сдвиге по циклу). Сдвиг по циклу в таблице перевозок преобразует любуе решения системы ограницений транспортной задачи (23), (24) также в решение этой системы.
Определение. Циклом пересчёта данной свободной клетки таблицы перевозок называется цикл, одна из вершин которого находится в этой свободной клетке, а остальные вершины в базисных клетках.
Заметим, что вершины цикла пересчёта могут и не занимать всех базисных клеток таблицы перевозок. Важно, что все вершины цикла, кроме одной, лежат в базисных клетках.
Теорема. Для любой свободной клетки в таблице перевозок существует, и притом единственный, цикл пересчёта.
Замечание. В дальнейшем цикл пересчёта свободной клетки будем считать означенным, причём свободной клетке будем приписывать знак «+».