2.2. Теореми додавання та множення ймовірностей

2.2.1. Короткі теоретичні відомості

Випадкові події утворюють повну групу несумісних подій, якщо внаслідок випробування одна з них з’явиться обов’язково.

Класичне означення ймовірності. Ймовірністю події називають відношення числа сприятливих цій події наслідків випробування до загальної кількості усіх рівно можливих несумісних елементарних подій, що утворюють повну групу:

.

Протилежною до події називають подію , яка полягає у тому, що подія не відбудеться у даному випробуванні.

Сума ймовірностей протилежних подій дорівнює одиниці:

Сума ймовірностей повної групи несумісних подій дорівнює одиниці:

Умовною ймовірністю називають ймовірність події при умові, що подія відбулася.

Добутком декількох подій називають подію, яка полягає у одночасній появі усіх цих подій.

Ймовірність одночасної появи декількох подій дорівнює добутку ймовірності однієї з них на умовні ймовірності усіх інших, причому ймовірність кожної наступної події обчислюється у припущенні, що усі попередні події уже відбулися:

Подію називають незалежною від події , якщо поява події не змінює ймовірності події , тобто умовна ймовірність події дорівнює безумовній:

Декілька подій називають незалежними у сукупності (або просто незалежними), якщо незалежні кожні дві з них, а також незалежними є кожна подія і всі можливі добутки інших подій.

Ймовірність одночасної появи декількох незалежних подій дорівнює добутку ймовірностей цих подій:

Події називають несумісними, якщо поява однієї з них виключає появу інших подій у цьому ж випробуванні.

Сумою декількох подій називають подію, яка полягає у появі хоча б однієї з цих подій.

Якщо випадкові події є попарно несумісними, то ймовірність появи хоча б однієї з них дорівнює сумі їх ймовірностей:

2. Приклади розв’язування завдань

Задача 2.1. У ящику п’ять білих і десять чорних кульок. Навмання виймають дві кульки. Знайти ймовірність того, що серед них:

а) обидві кульки білі;

б) обидві кульки чорні;

в) обидві кульки однакового кольору;

г) дістали кульки різних кольорів

д) хоча б одна кулька біла.

Розв’язання:

Перший спосіб.

Задачу можна розв’язати користуючись класичним означенням ймовірності та правилами комбінаторики.

Міркування можуть бути такими: 2 кульки із 15 можна вибрати способами. Таким чином у випробуванні, що розглядається, всього елементарних подій.

а) Нехай подія – обидві вийняті кульки є білими. Тоді події сприяє елементарних подій, бо 2 кульки з 5 можна вибрати способами.

Таким чином за класичним означенням ймовірності:

.

б) Нехай подія – обидві вийняті кульки є чорними. Тоді події сприяє елементарних подій:

в) Нехай подія – вийняли кульки однакового кольору. Зрозуміло, що вони можуть бути або білими (подія ), або чорними (подія ).

Події сприяє елементарних подій, а події - елементарних подій. Тоді за комбінаторним правилом додавання події сприяє + елементарних подій, тому

.

г) Нехай подія – вийняли кульки різних кольорів. Зрозуміло, що одна з них біла (подія ), а інша - чорна (подія ).

Події сприяє елементарних подій, а події - елементарних подій. Тоді за комбінаторним правилом множення події сприяє елементарних подій, тому

.

д) Нехай подія – вийняли хоча одну білу кульку. Тоді - не вийняли жодної білої кульки, тобто обидві вийняті кульки є чорними.

Події сприяє елементарних подій:

.

Другий спосіб.

Задачу можна розв’язати користуючись теоремами додавання та множення ймовірностей. Міркування можуть бути такими: одночасне взяття двох кульок можна розглядати як послідовне взяття двох кульок одна за одною.

а) Нехай подія – обидві вийняті кульки є білими. Тобто перша витягнута кулька є білою (подія ) і друга витягнута кулька є білою (подія ). Тоді подія є добутком подій і :

.

б) Нехай подія – обидві вийняті кульки є чорними. Тобто перша витягнута кулька є чорною (подія ) і друга витягнута кулька є чорною (подія ). Тоді подія є добутком подій і :

.

в) Нехай подія – вийняли кульки однакового кольору. Зрозуміло, що вони можуть бути або білими (подія ), або чорними (подія ). Тоді подія є сумою подій і , які є несумісними:

г) Нехай подія – вийняли кульки різних кольорів. Зрозуміло, що одна з них біла, а інша - чорна.

Подію можна розглядати як суму двох несумісних подій і , де - першою вийняли чорну кульку, а потім білу;

- першою вийняли білу кульку, а потім чорну.

Таким чином:

д) Нехай подія – вийняли хоча одну білу кульку. Тоді - не вийняли жодної білої кульки, тобто обидві вийняті кульки є чорними.

.

Відповідь: а) ; б) ; в) ; г) ; д) .

Задача 2.2. Ймовірність влучення в ціль для першого стрільця дорівнює 0,8; для другого – 0,9; для третього – 0,75. Кожен із стрільців зробив один постріл. Знайти ймовірність того, що:

а) усі стрільці влучать;

б) усі стрільці не влучать;

в) у ціль влучить один стрілець;

г) хоча б один із стрільців влучить в ціль;

д) два стрільці з трьох влучать в ціль.

Розв’язання: нехай подія - влучення і-м стрільцем (і=1,2,3). Розв’яжемо задачу користуючись теоремами додавання та множення ймовірностей.

а) Нехай подія – усі три стрільці влучать у ціль. Її можна розглядати як добуток трьох незалежних подій , та :

.

б) Нехай подія – усі три стрільці не влучать у ціль. Її можна розглядати як добуток трьох незалежних подій , та :

.

в) Нехай подія – у ціль влучить лише один стрілець: або лише перший, або лише другий, або лише третій. Її можна розглядати як суму трьох несумісних подій , та , де

-у ціль влучить лише перший стрілець;

-у ціль влучить лише другий стрілець;

-у ціль влучить лише третій стрілець.

Тоді:

г) Нехай подія – хоча б один із стрільців влучить в ціль. Тоді - жоден із стрільців не влучить у ціль.

д) Нехай подія – лише два стрільці з трьох влучать в ціль. Її можна розглядати як суму трьох несумісних подій , та , де

-у ціль влучить лише перший та другий стрілець;

-у ціль влучить лише другий та третій стрілець;

-у ціль влучить лише перший та третій стрілець.

Тоді:

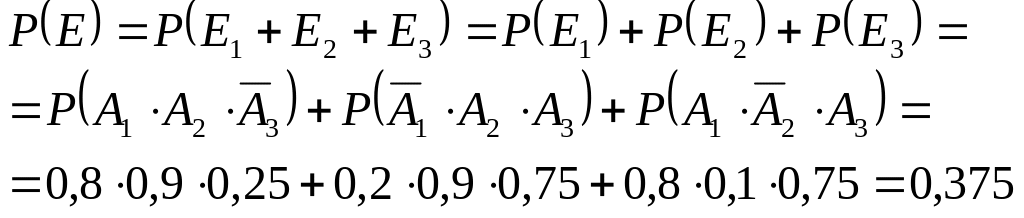
Відповідь: а) ; б) ; в) ; г) ; д) .