3.1. Частинні похідні Приклади розв’язування завдань

Задача № 4 . Нехай задана функція декількох змінних , знайти та .

Розв’язання:

Слід пам’ятати, що при диференціюванні функції двох змінних за змінною змінну треба вважати константою та навпаки, при диференціюванні за змінною змінну треба розглядати як сталу величину.

Отже,

вважаємо, що

Відомо, що при диференціюванні функції двох змінних справедливою є формула:

тому

Відповідь: ; .

3.2. Локальні екстремуми функції двох змінних Приклади розв’язування завдань

Задача № 5. Дослідити функцію на екстремум.

Розв’язання:

Відомо, що екстремуми функції шукають серед її стаціонарних точок. Стаціонарні точки функції знаходять, побудувавши та розв’язавши систему рівнянь:

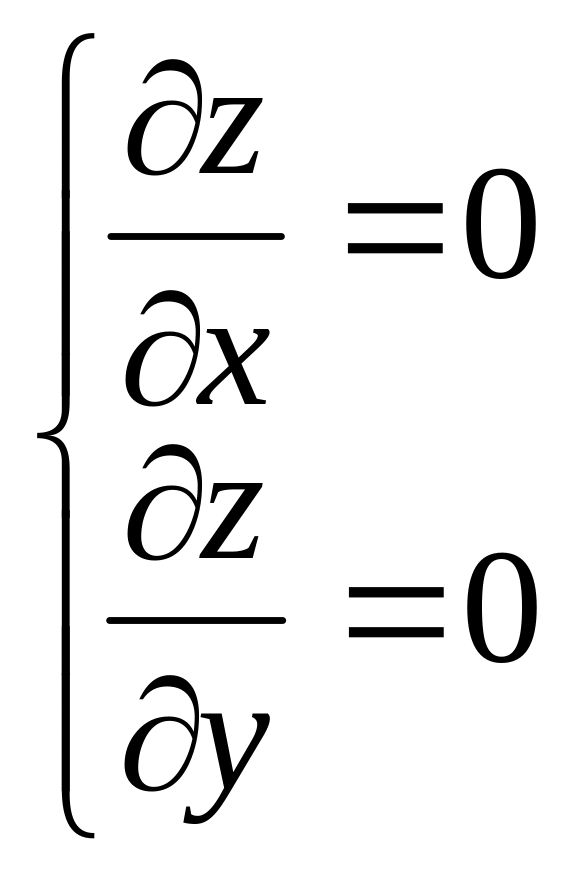
Знайдемо частинні похідні функції :

Побудуємо та розв’яжемо відповідну систему рівнянь, прирівнявши отримані частинні похідні до нуля:

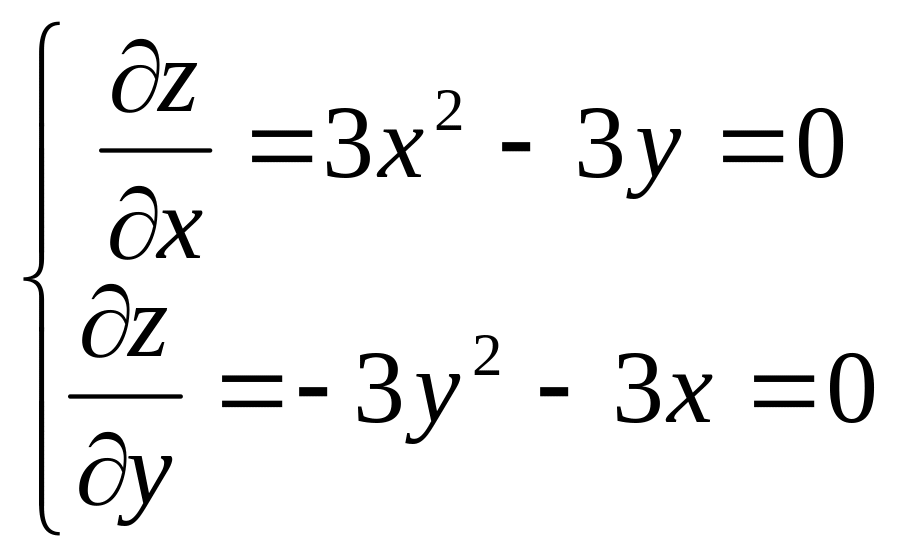
Таким чином отримали дві стаціонарні точки та . Для того щоб з’ясувати питання чи є ці точки екстремумами необхідно обчислити визначник та зробити відповідні висновки:

Знайдемо частинні похідні другого порядку функції :

Таким чином:

Перевіримо виконання достатніх умов екстремуму в кожній із стаціонарних точок, тобто обчислимо значення визначника у точках та :

Так як то точка не є точкою екстремуму.

Так як то точка є точкою екстремуму. З’ясуємо якою саме. Для цього необхідно з’ясувати знак у цій точці:

Таким чином точка є точкою максимуму функції . Обчислимо значення функції у цій точці:

Відповідь:

РОЗДІЛ 4. Методичні вказівки до розв’язання завдань з розділу «Інтегральне числення функцій однієї змінної»

1. Таблиця та основні властивості інтегралів. Основні методи інтегрування

Приклади розв’язування завдань

Задача 6. Знайти інтеграли, користуючись таблицею інтегралів, властивостями та найпростішими правилами інтегрування.

Розв’язання:

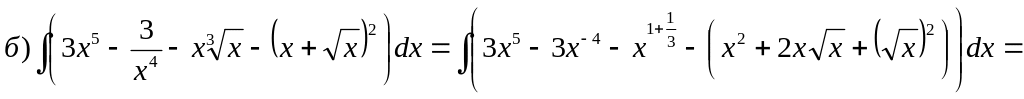
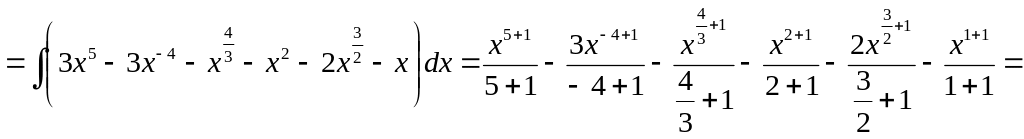
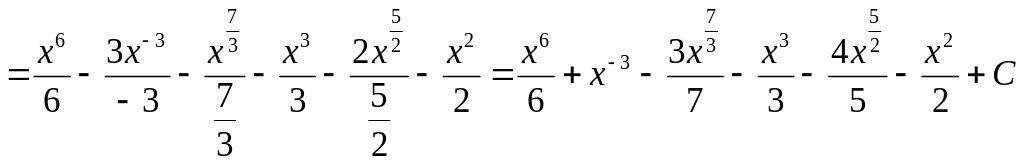
Відповідь: а) ;

б) ; в) ;

г) .

2. Інтегрування деяких раціональних функцій Приклади розв’язування завдань

Задача 7. Знайти інтеграли від функцій, які містять квадратний тричлен (а) та від раціональних дробів (б).

Розв’язання.

Для зручності виконання подальших дій, позбавимось від коефіцієнту при :

Виділимо у знаменнику з квадратного тричлена повний квадрат, тобто скористаємось формулою:

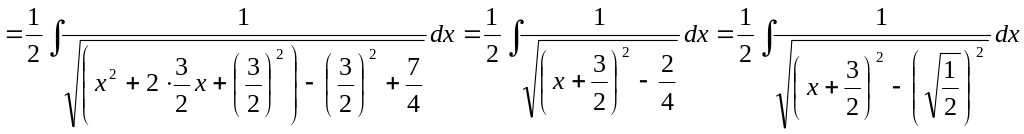
У таблиці інтегралів знайдемо відповідну формулу. Вона має такий вигляд:

Використаємо зазначену формулу:

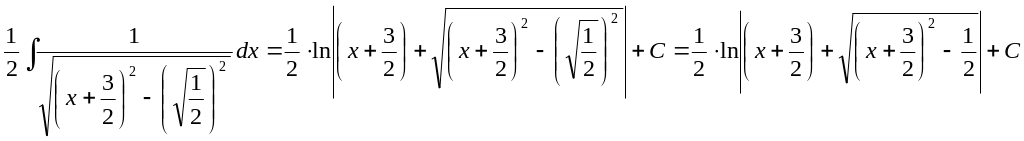
Підінтегральний раціональний дріб є правильним. Зведемо його до суми елементарних дробів методом невизначених коефіцієнтів.

Розкладемо знаменник на найпростіші дійсні множники:

Тоді

Для знаходження невідомих коефіцієнтів приведемо ліву частину виразу до спільного знаменника:

Складемо систему рівнянь для визначення невідомих коефіцієнтів , прирівнявши коефіцієнти при однакових степенях :

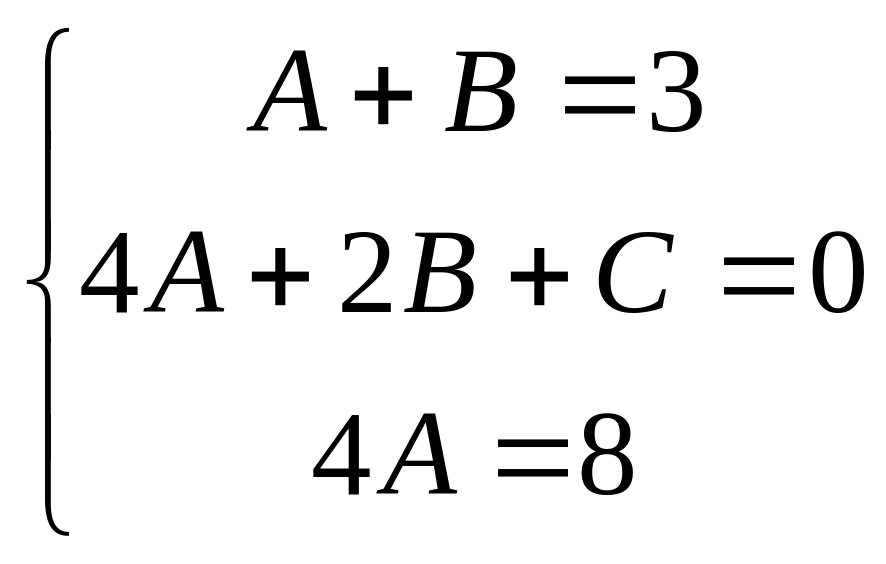
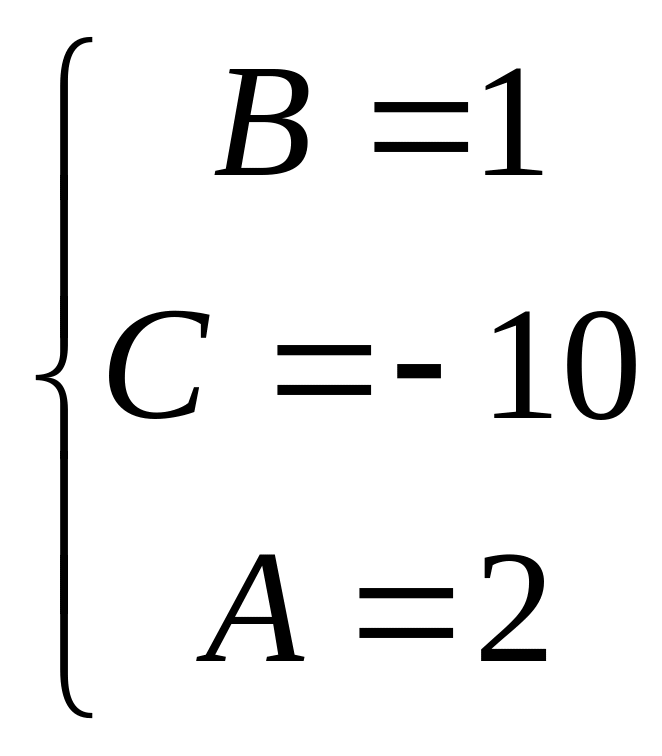
Таким чином отримуємо

Відповідь: а) ; б)