Київська державна академія водного транспорту

імені гетьмана Петра Конашевича-Сагайдачного

ВИЩА МАТЕМАТИКА

(Диференціальне та інтегральне числення)

Методичні вказівки до виконання контрольної роботи №2

Для студентів першого курсу заочної форми навчання

напряму підготовки «Облік та аудит»

Київ 2012

ЗМІСТ

ВСТУП……………………………………………………………………	3
РОЗДІЛ 1. Методичні вказівки щодо оформлення контрольних робіт 1.1. Вибір варіанту контрольної роботи…………………………………... 1.2. Оформлення титульної сторінки…………...……………………......	4 4
РОЗДІЛ 2. Методичні вказівки до розв’язання завдань з розділу «Диференціальне числення функцій однієї змінної» Диференціювання функцій………………………………….......... Правило Лопіталя………………………………………………….. Застосування диференціального числення для дослідження функцій……………………………………………………………….	5 7 8
РОЗДІЛ 3. Методичні вказівки до розв’язання завдань з розділу «Диференціальне числення функцій багатьох змінної» 3.1. Частинні похідні……..………………………………………………. 3.2. Локальні екстремуми функції двох змінних……………………….	12 13
РОЗДІЛ 4. Методичні вказівки до розв’язання завдань з розділу «Інтегральне числення функцій однієї змінної» Таблиця та основні властивості інтегралів. Основні методи інтегрування…………………………………………………………. Інтегрування деяких раціональних функцій…………….………… Інтегрування деяких тригонометричних функцій………………… Визначений інтеграл………………………………………………… Застосування визначеного інтегралу до обчислення площ……….	15 16 17 19 20
РОЗДІЛ 5 . Завдання для індивідуального виконання…………………..	22
ЛІТЕРАТУРА………………………………………………………………	37

ВСТУП

РОЗДІЛ 1. Методичні вказівки щодо оформлення контрольних робіт

1.1. Вибір варіанту контрольної роботи

Варіант контрольної роботи визначають з наведеної далі таблиці за останніми двома цифрами шифру (номеру залікової книжки):

		передостання цифра шифру
		0	1	2	3	4	5	6	7	8	9
остання цифра шифру	0	10	1	2	3	4	5	6	7	8	9
	1	10	11	12	13	14	15	16	17	18	19
	2	20	21	22	23	24	25	26	27	28	29
	3	30	1	2	3	4	5	6	7	8	9
	4	10	11	12	13	14	15	16	17	18	19
	5	20	21	22	23	24	25	26	27	28	29
	6	30	1	2	3	4	5	6	7	8	9
	7	10	11	12	13	14	15	16	17	18	19
	8	20	21	22	23	24	25	26	27	28	29
	9	10	11	12	13	14	15	16	17	18	19

Наприклад, шифру 047252 відповідає варіант № 25. Отже, студент із таким шифром в кожній задачі мусить виконати завдання із номером 25.

1.2. Оформлення титульної сторінки

Перед виконанням контрольної роботи студент повинен вивчити відповідні розділи курсу “Вища математика ” за навчальними посібниками та підручниками з цієї дисципліни.

Кожна контрольна робота виконується в окремому зошиті, титульну сторінку оформлюють за зразком:

Київська державна академія водного транспорту

Контрольна робота з курсу

“Вища математика”

Виконав: Півчук Олексій Володимирович

Форма навчання: заочна

Курс: 1

Спеціальність: “Судоводіння на внутрішніх

водних шляхах”

Шифр (номер залікової книжки): 047252

Варіант: 25 варіант

РОЗДІЛ 2. Методичні вказівки до розв’язання завдань з розділу «Диференціальне числення функцій однієї змінної»

1. Диференціювання функцій Приклади розв’язування завдань

Задача № 1. Знайти похідні першого порядку функцій.

а)	в)
б)	г)
д)

Розв’язання:

а) Для диференціювання функції застосуємо таблицю похідних, а також правило диференціювання добутку та частки, тобто формули:

Тоді:

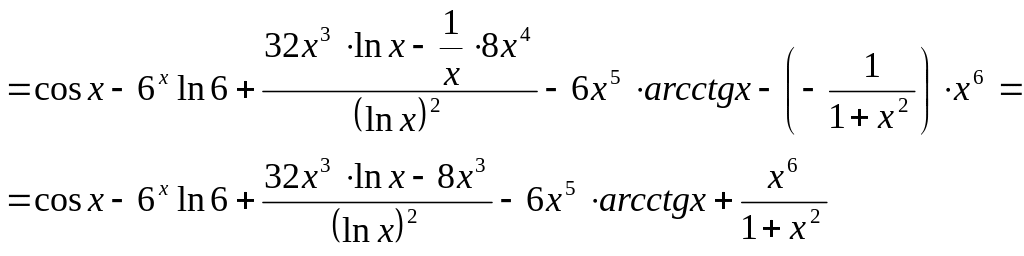
б) Для диференціювання функції застосуємо правило диференціювання складеної функції:

.

в) Для відшукання похідної функції застосуємо метод логарифмічного диференціювання. Логарифмуючи рівність за основою е, дістанемо

.

За властивістю логарифмів отримуємо:

.

Продиференціюємо обидві частини рівності, зважаючи на те що є функцією від :

.

Застосуємо правило диференціювання добутку:

,

Помножимо обидві частини рівності на :

г) Щоб продиференціювати неявно задану функцію потрібно взяти похідну по від обох частин рівності, вважаючи функцією від :

Застосуємо правило диференціювання складеної функції (для лівої частини рівності), а також правило диференціювання добутку (для правої частини рівності):

Одержане рівняння розв’яжемо відносно :

д) Відомо, що похідну функції заданої параметрично знаходять за формулою:

, де

Тоді:

Відповідь: а) ;

б) ; в) ; г) ; д) .