1. Пряма на площині Приклади розв’язування завдань

Задача № 5. Задані вершини трикутника АВС, де .Знайти:

а) рівняння та довжину сторони АВ;

б) рівняння та довжину висоти СН;

в) рівняння прямої, що проходить через точку С паралельно до сторони АВ;

г) виконати відповідні креслення до завдань а-в.

Розв’язання:

а) Відомо координати двох точок, які належать прямій АВ: . Тому складемо рівняння прямої АВ за двома точками , тобто використовуючи формулу:

.

Тоді

Обчислимо довжину сторони АВ, як довжину відповідного вектора , тобто за формулою:

, де - початок і кінець вектора .

Тоді

б) Пряма СН є перпендикулярною до прямої АВ. Тому нормальний вектор прямої АВ є напрямним вектором для прямої СН, тобто .

З’ясувавши координати цього вектора, а також знаючи координати точки можемо скласти канонічне рівняння прямої СН за точкою та напрямним вектором , тобто використовуючи формулу:

Знайдемо координати вектора із рівняння прямої АВ, пам’ятаючи, що якщо пряма має рівняння , то її нормальний вектор має координати .

Перетворимо рівняння прямої АВ із канонічного вигляду до загального:

, звідки випливає, що .

Складемо рівняння прямої СН за точкою та напрямним вектором :

Довжину висоти СН обчислимо, як відстань від точки до прямою , тобто за формулою:

Тоді відстань від точки до прямою дорівнюватиме:

.

в) Пряму, що проходить через точку С паралельно до сторони АВ позначимо l. Так як пряма l є паралельною до прямої АВ, то нормальний вектор прямої АВ є нормальним вектором і для прямої l, тобто .

З’ясувавши координати цього вектора, а також знаючи координати точки можемо скласти рівняння прямої l за точкою та нормальним вектором , тобто використовуючи формулу:

Знайдемо координати вектора із рівняння прямої АВ:

, тому .

Складемо рівняння прямої l за точкою та нормальним вектором :

г)

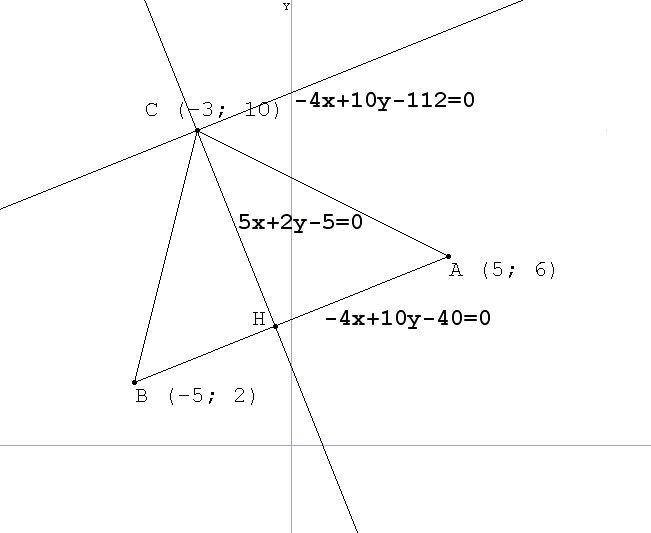
Відповідь: а) ; ; б) ; ; в) .

2. Прямі та площини у просторі Приклади розв’язування завдань

Задача № 6. Задані чотири точки , , , . Знайти:

а) рівняння площини А₁А₂А₃;

б) рівняння прямої А₁А₄;

в) відстань від точки А₄ до площини А₁А₂А₃;

г)кут між прямою А₁А₄ та площиною А₁А₂А₃;

д) рівняння прямої, що проходить через точку А₄ перпендикулярно площині А₁А₂А₃;

е) рівняння площини, що проходить через точку А₄ перпендикулярно до прямої А₁А₂.

Розв’язання:

а) Відомо координати трьох точок, які належать площині А₁А₂А_3. Тому будемо шукати її рівняння, як рівняння площини за трьома точками , , , тобто за формулою:

Складемо рівняння площини А₁А₂А₃ за трьома точками , , :

Таким чином

б) Відомо координати двох точок, які належать прямій А₁А₄: , . Тому складемо рівняння прямої А₁А₄ за двома точками , тобто використовуючи формулу:

.

Тоді

в) Відстань від точки до площини знаходять за формулою:

Тоді відстань від точки до площини дорівнюватиме:

.

г) Кут між прямою та площиною знаходять за формулою:

,

де - координати напрямного вектора прямої, - координати нормального вектора площини.

Із канонічного рівняння прямої можна знайти координати її напрямного вектора . Тому координати напрямного вектора прямої дорівнюватимуть .

Із загального рівняння площини можна знайти координати її нормального вектора . Тому координати нормального вектора площини дорівнюватимуть .

Знайдемо кут між прямою та площиною знаходять за формулою:

д) Назвемо прямою l пряму, що проходить через точку перпендикулярно площині А₁А₂А₃.

Так як пряма l є перпендикулярною до площини А₁А₂А₃, то нормальний вектор площини А₁А₂А₃ є напрямним вектором для прямої l, тобто .

Знаючи координати цього вектора , а також координати точки , можемо скласти рівняння прямої l за точкою та напрямним вектором , тобто використовуючи формулу:

Тоді

е) Назвемо площину, що проходить через точку А₄ перпендикулярно до прямої А₁А₂.

Так як пряма А₁А₂ є перпендикулярною до площини , то вектор можна вважати нормальним вектором площини . Обчислимо координати вектора :

, тобто

Знаючи координати цього вектора , а також координати точки , можемо скласти рівняння площини за точкою та нормальним вектором , тобто використовуючи формулу:

Тоді:

Відповідь: а) ; б) ; в) ; г) ; д) ; е) .

РОЗДІЛ 5. Методичні вказівки до розв’язання завдань з розділу «Вступ до математичного аналізу»