Поверхностные волны Рэлея.

Рассмотрим упругое полупространство. Начало координат поместим на его поверхности, ось направим вдоль границы, ось — вглубь среды (рис. 1).

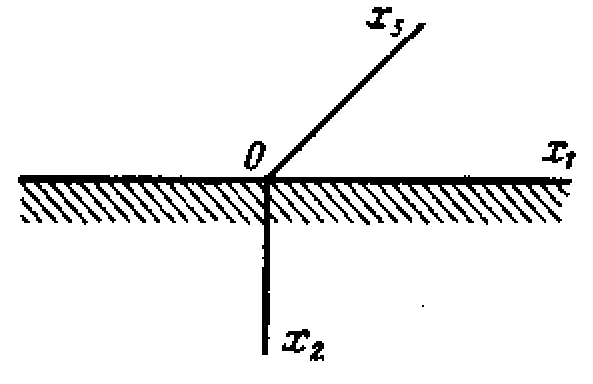
Рис.1.

Предполагается, что объемные силы отсутствуют. Будем искать решение уравнений (4а) и (4б), которое не зависит от (плоская деформация), во времени меняется по синусоидальному закону, затухает с глубиной, а на границе удовлетворяет условиям

. (25)

Это — задача о свободных колебаниях полупространства. Решение попытаемся найти в виде

(26)

Здесь — заданная частота. Постоянные , , (фазовая скорость), , должны быть подобраны так, чтобы (26) удовлетворяло уравнениям (4а), (4б) и граничным условиям (25).

Для определения фазовой скорости получим уравнение

,

где

.

Важно подчеркнуть, что фазовая скорость не зависит от частоты , а зависит лишь от отношения .

Мы построили решение в комплексной форме, но поскольку уравнения и краевые условия задачи линейные, ее решением будет как действительная, так и мнимая часть получаемых выражений; например,

(27)

Так как коэффициенты и , характеризующие затухание с глубиной, растут с увеличением частоты , то в силу (27) приходим к выводу, что чем волна длиннее, тем на большей глубине она ощущается.

При из (27) получаем

Отсюда следует, что точки поверхности движутся по эллипсам.

Рассмотренные выше волны были впервые изучены Рэлеем. Они наблюдаются вдали от источника возмущения. Поскольку энергия, которую эти волны несут, сконцентрирована у поверхности и рассеивается по поверхности, то ее рассеивание происходит медленнее, чем в волнах, где энергия рассеивается по объему возмущенной области. Поэтому при землетрясениях для наблюдателя, удаленного от эпицентра, наибольшую опасность представляют рэлеевские волны.