5.2. Линейные операции над векторами

Под линейными операциями над векторамипонимают операции сложенияи вычитания векторов, а также умножение векторана число.

Пусть а и b — два произвольных вектора. Возьмем произвольную точку О и построим вектор ОА=а. От точки А отложим вектор АВ = b . Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b : О B=а+b (см. рис. 2)

.

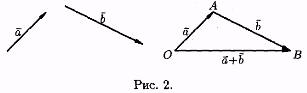Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелoграмма (см. рис. 3).

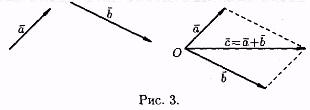
На рисунке 4 показано сложение трех векторов а, b и с.

 

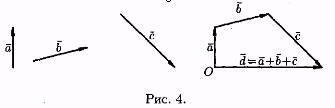
Под разностью векторов а и b понимается вектор с=а-b такой, что b+с=а (см. рис. 5).

 

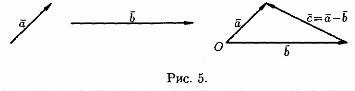
Отметим, что в параллелограмме, построенном на векторах а и b одна направленная диагональ является суммой векторов а и b, а другая — разностью (см. рис. 6).

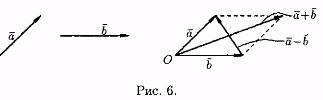
Можно вычитать векторы по правилу: а - b = а + (-b ), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным векторуb.

Произведением вектора а на скаляр (число) λ  называется вектор λ*а (или а*λ), который имеет длину    |λ|*|а|, коллинеаренвектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0. Из определения произведения вектора на число следуют свойства этого произведения:

1) если b=λ * а , то b || а . Наоборот, если b||а , (а0 ), то при некотором λ  верно равенство b=λа ;

2) всегда а =|а| • а^-о , т. е. каждый вектор равен произведению его мо дуля на орт.

Линейные операции над векторами обладают следующими свойствами:

1. а+b=b+а 2. (а +b) +с=а + (b +с), 3.λ1 • (λ2 •а) =λ1 •λ2 •а, 4.(λ1 +λ2) •а =λ1 •а +λ2 •а, 5. λ • (а +b) =λ •а+λ •b.

Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.

5.3. Проекция вектора на ось

Пусть в пространстве задана ось l, т. е. направленная прямая.

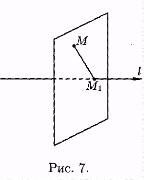
Проекцией точки М на ось l называется основание М₁ перпендикуляра ММ₁, опущенного из точки на ось.

Точка М₁ есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).

Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.

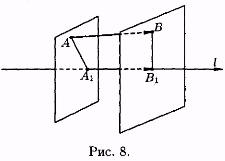
_{Пусть АВ — произвольный} вектор (АВ 0). Обозначим через А₁ и b ₁проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим вектор А₁В₁

Проекцией вектора АВ на ось l называет ся положительное число |A ₁B ₁ | , если вектор А₁В ₁ и ось l одинаково направлены и отрица тельное число — |A ₁B ₁ | , если вектор А ₁В₁ и ось l противоположно направлены (см. рис. 8). Если точки a ₁и b ₁совпадают (А ₁В ₁ =0), то проекция вектора АВ равна 0.

Проекция вектора АВ на ось l обозначается так: пр_lАВ. Если АВ=0 или АВl , то пр_l АВ=0.

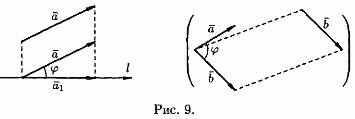
Угол   между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,

Рассмотрим некоторые основные свойства проекций.

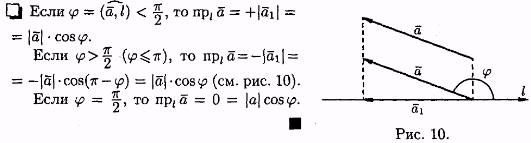
Свойство 1. Проекция вектораa на ось l равна произведению модуля вектора a на косинус угла   между вектором и осью, т. е. пр_la =|a |•cos .

Следствие 5.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.

Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.

Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось

Свойство 3. При умножении вектора а на число А его проекция на ось также умножается на это число, т. е.

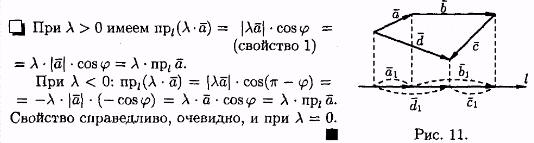
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.

5.4. Разложение вектора по ортам координатных осей.  Модуль вектора. Направляющие косинусы.

Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i , j , k соответственно (см. рис. 12).

 

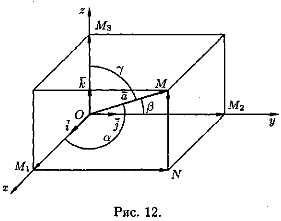
Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ.

Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М₁ , М₂ и Мз.Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр_ха=|OM ₁|, np_ya = |ОМ₂|, пр_z а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ ₁ + M₁N + NM.

А так как M ₁N=OM ₂ , NM =ОМз, то

а=ОМ ₁ + ОМ ₂ + ОМ₃                                             (5.1)

 

Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через а_х, а_у и a_z, т.е. |OM₁| = а_х,|ОМ₂| = а_у, |ОМ₃| = а_z. Тогда из равенств (5.1) и (5.2) получаем

a=a_xi+a_yj+a_zk            (5.3)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_у, a_z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.

Векторное равенство (5.3) часто записывают в символическом виде: a = (a_x ;a_y ;a_z).

Равенство b = (b_x ;b_y ; b_z ) означает, что b = b_х•i +b _у • j + b_z • k . Зная проекции вектора а, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать

  

Отсюда

т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны . По свойству проекции вектора на ось, имеем

Или, что то же самое,

Числа   называются направляющими косинусами вектора а.

Подставим выражения (5.5) в равенство (5.4), получаем

Сократив на получим соотношение

т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

Легко заметить, что координатами единичного вектораe являются числа

Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.