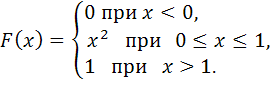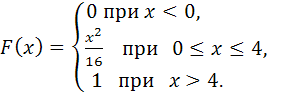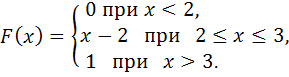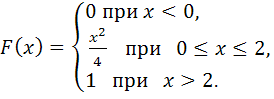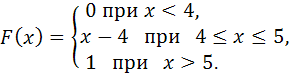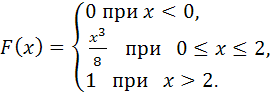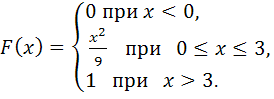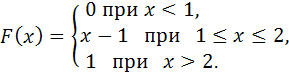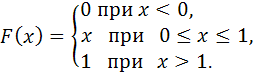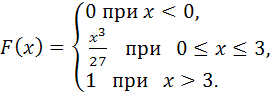Задачи для контрольных заданий
1-5.
В
книге 
страниц. Чему равна вероятность того,
что наугад открытая страница будет
иметь порядковый номер, кратный 
?
6-10.
В
урне 
красных и 
зеленых шаров. Из урны извлекается один
шар. Какова вероятность того, что
извлеченный шар окажется зеленым?
11-15.
Наудачу
выбрано число, не превосходящее
.
Какова вероятность того, что это число
кратно 
?
16-20. В урне белых и черных шаров. Из урны вынимают сразу шаров. Найти вероятность того, что шаров будут белыми, а остальные черными?
21-25.
В
партии, состоящей из
изделий, имеется 
дефектных. Из партии выбирается для
контроля 
изделий. Найти вероятность того, что из
них ровно 
изделий будет дефектными.
26-30. Среди студентов группы, в которой девушек, разыгрывается билетов. Найти вероятность того, что среди обладателей билетов окажутся девушек.
31-35.
Вероятность
попадания в мишень для первого спортсмена
,
а для второго - 
.
Спортсмены независимо друг от друга
сделали по одному выстрелу. Найти
вероятность того, что в мишень попадет
хотя бы один спортсмен.
36-40.
Мастер обслуживает 
станков. 
%
рабочего времени он проводит у первого
станка, 
%
- у второго, 
%
- у третьего, 
%
- у четвертого, 
%
- у пятого. Найти вероятность того, что
в наудачу выбранный момент времени он
находится:
у первого или у второго, или у четвертого, если
у второго или у третьего, или у пятого, если
у первого или у четвертого, или у пятого, если
у второго или у третьего, или у четвертого, если
у третьего или у четвертого, или у пятого, если
41-45. В урне находится красных и синих шаров. Из урны последовательно без возвращения извлекается три шара. Найти вероятность того, что все три шара синие.
46-50.
В
каждом из трех ящиков находится по 
деталей. В первом ящике 
,
во втором 
,
в третьем 
стандартных деталей. Из каждого ящика
наудачу вынимают по одной детали. Какова
вероятность того. Что все три вынутые
детали окажутся стандартными.
51-55.Вероятность
правильного оформления счета на
предприятии составляет 
.
Во время аудиторской проверки были
взяты два счета. Какова вероятность
того, что только один из них оформлен
правильно?
56-60.
На
фабрике изготовляющей болты, первая
машина производит
%,
вторая -
%,
третья -
%
всех изделий. Брак в их продукции
составляет соответственно 
%,
%,
%.
Найти вероятность того, что случайно
выбранный болт оказался дефектным.
61-65. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает % брака, второй - %, третий- %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило , со второго - и с третьего - деталей.
66-70. На предприятии изготавливаются изделия определенного вида на трех поточных линиях. На первой линии производится % изделий от общего объема их производства, на второй - %, на третий - %. Каждая из линий характеризуется соответственно следующими процентами годности изделий: %, %, %. Определить вероятность того, что наугад взятое изделие, выпущенное предприятием, окажется бракованным.
71-75. Вероятность попадания в цель при одном выстреле равна . Производится выстрелов. Найти вероятность того, что цель будет поражена раз.
76-80. Всхожесть семян пшеницы составляет %. Определить вероятность того, что из посеянных семян взойдет .
81-85. Монета подбрасывается раз. Найти вероятность того, что выпадет ровно гербов.
86-90. Вероятность изготовления детали первого сорта на данном станке равно . Найти вероятность того, что среди наугад взятых деталей окажется деталей первого сорта.
91-95. Вероятность того, что семя злака прорастет равна . Найти вероятность того, что из посеянных семян прорастет ровно семян.
96-105.
Дана
вероятность
проявления события 
в каждом из
независимых испытаний. Найти вероятность
того, что в этих испытаниях событие
проявится не менее
раз и не более
раз.
106-115. Задан закон распределения дискретной случайной величины (в первой строке указаны возможные значения случайной величины , во второй строке даны вероятности этих значений).
Найти:
1) математическое ожидание 
;
2) дисперсию 
;
3) среднее квадратическое отклонение
.
-
8
4
6
5
p
0,1
0,3
0,2
0,4
-
23
25
27
29
p
0,2
0,1
0,3
0,4
-
10
8
6
9
p
0,4
0,1
0,3
0,2
-
32
40
37
35
p
0,1
0,3
0,4
0,2
-
42
41
43
45
p
0,3
0,3
0,2
0,2
-
15
11
13
12
p
0,2
0,5
0,2
0,1
-
52
54
57
51
p
0,1
0,4
0,3
0,2
-
21
20
22
26
p
0,5
0,2
0,2
0,1
-
34
30
32
36
p
0,2
0,4
0,3
0,1
|
50 |
48 |
51 |
53 |
p |
0,3 |
0,2 |
0,2 |
0,3 |
116-125.
Случайная
величина
задана своей функцией распределения
.
Найти: 1) функцию плотности вероятностей
;
2) математическое ожидание
;
3) дисперсию
.
126-130.
Случайная
величина
распределена по нормальному закону,
причем 
,
.
Найти:
131-135. Средний вес клубня картофеля равен г. Какова вероятность того, что наугад взятый клубень картофеля весит не более г.?
136-140. Среднее число молодых специалистов, ежегодно направляемых в аспирантуру, составляет человек. Оценить вероятность того, что в данном году будет направлено в аспирантуру не более молодых специалистов.
141-145. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно . Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор будет не более .
146-150.
Случайная
величина
имеет дисперсию 
.
Какова вероятность того, что случайная
величина
отличается от
более
чем на 
151-155.
Среднее
значение длины детали равно
см, а дисперсия равна 
.
Оценить вероятность того, что изготовленная
деталь окажется по своей длине не меньше
см и не больше 
см.
156-165. Задана выборка:
100; 98+0,2N; 100,7; 99,7; 100,1-0,1N; 98,9; 100,8-0,1[N/2]; 98,6+0,1[N/2]; 101; 99,3; 102-0,2N; 100,8; 100,1; 99,6+0,1N; 101-0,1N; 101,5; 101,6-0,1N; 100,3; 99,6; 100+0,1N .
Составить точечный статистический ряд. Построить полигон. Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение.
Составить интервальный статистический ряд, взяв отрезок [97;105] с шагом h=1. Построить гистограмму. Найти выборочную среднюю и выборочную дисперсию.
166-170.
Известно, что случайная величина
имеет распределение Пуассона 
.
Неизвестным является параметр а.
Найти (методом моментов или методом
наибольшего правдоподобия) по реализации
выборки, представленной в таблице,
значения оценки неизвестного параметра
а.
-
xi
0
1
2
3
4
5
6
7
n
mi
N+1
N+2
N+3
N+4
N+5
N+6
N+7
N+8
10N
171-175.
Известно,
что случайная величина
имеет биномиальное распределение 
Неизвестным является параметр p.
Найти (методом моментов или методом
наибольшего правдоподобия) по реализации
выборки, представленной в таблице,
значения оценки неизвестного параметра
p.
-
xi
0
1
2
3
4
5
6
7
n
mi
N+1
N+2
N+3
N+4
N+5
N+6
N+7
N+8
10N
176-180. Случайная величина распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
-
xi
3
5
7
8
10
12
14
mi
N
2N
N+1
3N
N+2
4N
N+3
Найти
с надежностью 
доверительный интервал для оценки
математического ожидания.
181-185. Случайная величина распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
-
xi
3
5
7
8
10
12
14
mi
N
2N
N+1
3N
N+2
4N
N+3
Найти
с надежностью 
доверительный интервал для оценки
среднего квадратического отклонения.
186-190. Результаты измерения длин деталей машин, отобранных случайным образом, приведены ниже (в миллиметрах):
Длина детали |
xi |
503 |
504 |
505 |
506 |
507 |
508 |
509 |
510 |
511 |
512 |
Частота появления |
mi |
2N |
N+2 |
N |
N+4 |
2N-1 |
N |
N+5 |
N+3 |
2N-1 |
N |
Оценить
закон распределения случайной величины
- длины детали – для уровня значимости
.
