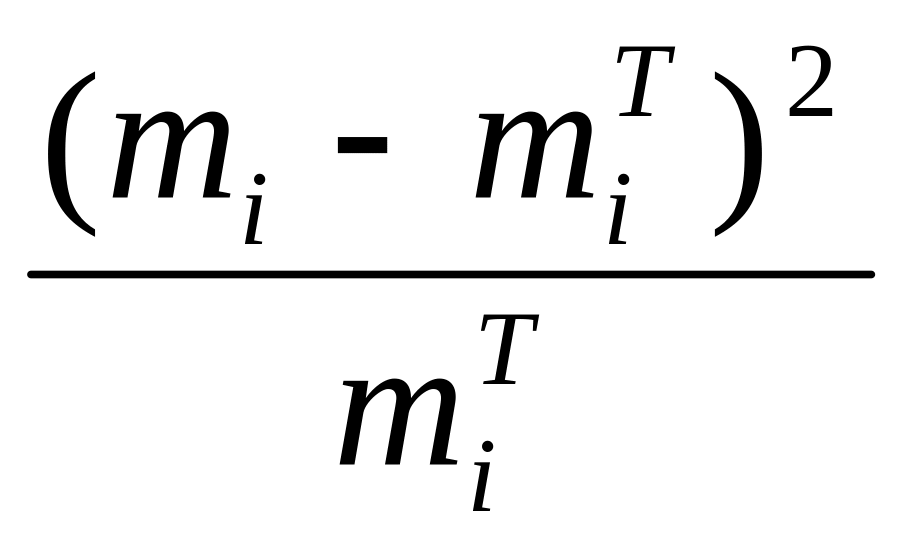МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФИЛИАЛ

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»

В Г. РОСЛАВЛЕ СМОЛЕНСКОЙ ОБЛАСТИ

(ФИЛИАЛ ФГБОУ ВПО «МГИУ» В Г. РОСЛАВЛЕ)

«УТВЕРЖДАЮ»

Зам. директора по учебной работе

__________________А. Н. Шитов

«___»___________________2012 г.

Теория вероятностей

и математическая статистика

Методические указания и контрольные задания

для студентов второго курса очной формы обучения

специальности 080100 («Экономика и управление»)

(III семестр)

Составитель:

старший преподаватель кафедры «ОМиЕНД», к. ф.-м. н.

Изотова О. А.

Рославль - 2012

ВВЕДЕНИЕ

Настоящие методические указания предназначены для студентов-очников, обучающихся по специальности 080100 («Экономика и управление») и охватывают материал разделов курса высшей математики «Теория вероятностей и математическая статистика».

Методические указания содержат образцы решения некоторых задач, контрольные задания.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задачи по «Теории вероятностей»

1. Найти вероятность того, что при бросании игральной кости выпадет число большее 4.

Решение. Пусть А – событие: выпадет цифра большая 4. Пусть Е_i – события: выпадет цифра под номером i. Тогда E₁, E₂, E₃, E₄, E₅, E₆ образуют группу элементарных событий. Количество всех элементарных событий n=6. Тогда А=Е₅+Е₆, m_A=2 и

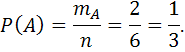
2. Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5?

Решение. Обозначим через А событие «число на взятой карточке кратно 5». В данном испытании имеется 30 элементарных событий, из которых событию А благоприятствует 6 событий (числа 5, 10, 15, 20, 25, 30). Следовательно,

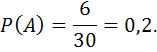
3. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.

Решение. Общее число возможных элементарных событий испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов

.

Определяем число событий, благоприятствующих событию А – «среди 6 взятых деталей 4 стандартных». Четыре стандартные детали из семи стандартных можно взять способами, при этом остальные 6 – 4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 – 7=3 нестандартных деталей можно способами. Следовательно, число благоприятствующих событий равно .

Искомая вероятность равна отношению числа событий, благоприятствующих событию А , к числу всех элементарных событий:

.

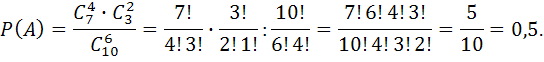
4. Монета бросается два раза. Найти вероятность того, что хотя бы один раз выпадет «орел».

Решение. Пусть А – событие: хотя бы один раз выпадет «орел». Тогда А₁ – событие: на 1-ом броске выпадет «орел», А₂ – событие: на 2-ом броске выпадет «орел». Очевидно, что А=А₁+А₂. Находим

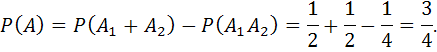
5. В урне 40 шариков: 15 синих, 5 зеленых и 20 белых. Какова вероятность того, что из урны будет извлечен синий или зеленый шарик?

Решение. Пусть А – событие: из урны будет извлечен цветной шарик. Через А₁ – событие: извлечен синий шарик, А₂ – событие: извлечен зеленый шарик. Тогда А=А₁+А₂, причем события А₁, А₂ несовместные. Получаем

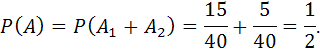
6. Подбрасывается игральный кубик. Чуму равна вероятность того, что выпадет четное число очков?

Решение. Введем обозначения: А – событие: выпало четное число очков; В_k – события: выпало k очков (k=1, 2, 3, 4, 5, 6). Событие А означает, что наступило хотя бы одно из событий: В₂, В₄, В₆ , т.е. А=В₂+В₄+В₆ . Поскольку события В₂, В₄, В₆ несовместны, то можно воспользоваться формулой

при n=3, учитывая, что В_k=1/6 (k=1, 2, 3, 4, 5, 6):

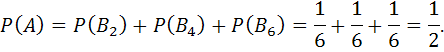
Замечание. Тот же результат получится и непосредственно по формуле

7. В коробке 10 шаров: 4 белых и 6 черных. По-очереди извлекаются два шара. Найти вероятность того, что оба шара белые.

Решение. Пусть А – событие: оба шара белые. Тогда А₁ – событие: 1-ый шар белый, А₂ – событие: 2-ой шар белый. Очевидно, что А=А₁А₂. Находим

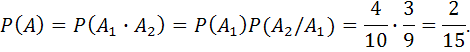
8. В коробке 4 белых и 6 черных шаров. Два раза извлекают по одному шару и каждый раз кладут его обратно. Найти вероятность того, что оба раза вытащили белый шар.

Решение. Пусть А – событие: оба раза вытащили белый шар. Тогда А₁ – событие: 1-ый раз вытащили белый шар, А₂ - событие: 2-ый раз вытащили белый шар. Очевидно, что А=А₁А₂, причем А₁ и А₂ независимые. Находим

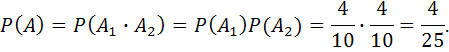
9. Слово папаха составлено из букв разрезной азбуки. Карточки с буквами тщательно перемешаны. Четыре карточки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить таким путем слово папа?

Решение. Обозначим через А, В, С, D соответственно события: извлечена первая, вторая, третья и четвертая буква слова папа из набора в 6 букв: а, а, а, п, п, х. Найдем вероятность событий: А, В/А, С/АВ, D/ABC.

; ; ; .

Тогда при n=4 получаем

.

10. В магазин поступают изделия с трех фабрик: 20% - с фабрики №1, 30% - с фабрики №2, 50% - с фабрики №3. Фабрика №1 допускает 1% брака, фабрика №2 допускает 2% брака, фабрика №3 допускает 0,5% брака. Случайным образом выбирается одно изделие. Найти вероятность того, что оно бракованное.

Решение. Пусть А – событие: выбранное изделие бракованное. Через H_i обозначим события: изделие поступило с фабрики № i (i=1,2,3), причем H₁, H₂, H₃ попарно несовместны. Тогда по формуле полной вероятности

11. Имеются две коробки с шарами. В 1-ой коробке содержится 99 белых шаров и 1 черный шар. Во 2-ой коробке содержится 1 белый шар и 99 черных шаров. Случайным образом выбирают коробку и достают один шар. Какова вероятность того, что это белый шар?

Решение. Пусть А – событие: достали белый шар. Тогда Н₁ – событие: выбрана коробка №1, Н₂ – событие: выбрана коробка №2. События Н₁ и Н₂ равновероятные, т.е.

.

Тогда

.

12. Производится 10 выстрелов по мишени. Вероятность попадания при каждом выстреле 0,9. Найти вероятность того, что будет ровно 7 попаданий.

Решение. В качестве испытания рассмотрим выстрел, в качестве события А – попадание в цель. Получим схему Бернулли из n=10 испытаний, р=0,9. Требуется найти P₁₀(7):

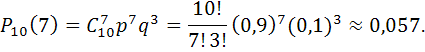
13. Испытывается 100 приборов. Вероятность того, что прибор не пройдет испытание равна 0,2. Найти вероятность того, что испытание пройдет не менее 72 приборов.

Решение. По условию n=100, p=0,2, q=0,8. Требуется найти вероятность того, что испытание не пройдет 28 или меньше приборов, т.е.

Тогда

В результате

14. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.

Решение. Вероятность того, что семья имеет холодильник, равна Т.к. n=400 достаточно велико (npq=64 ), то

Тогда

Замечание. Весьма малое значение вероятности не должно вызывать сомнения, т.к. кроме события «ровно 300 семей из 400 имеют холодильники» возможно еще 400 событий: «0 из 400», «1 из 400»,…, «400 из 400» со своими вероятностями. Все вместе эти события образуют полную группу, a значит, сумма их вероятностей равна 1.

15. Найти математическое ожидание дискретной случайной величины 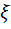, закон распределения которой задан таблицей

	3	4	5	6	7
р	0,1	0,2	0,4	0,2	0,1

Решение. Воспользуемся формулой :

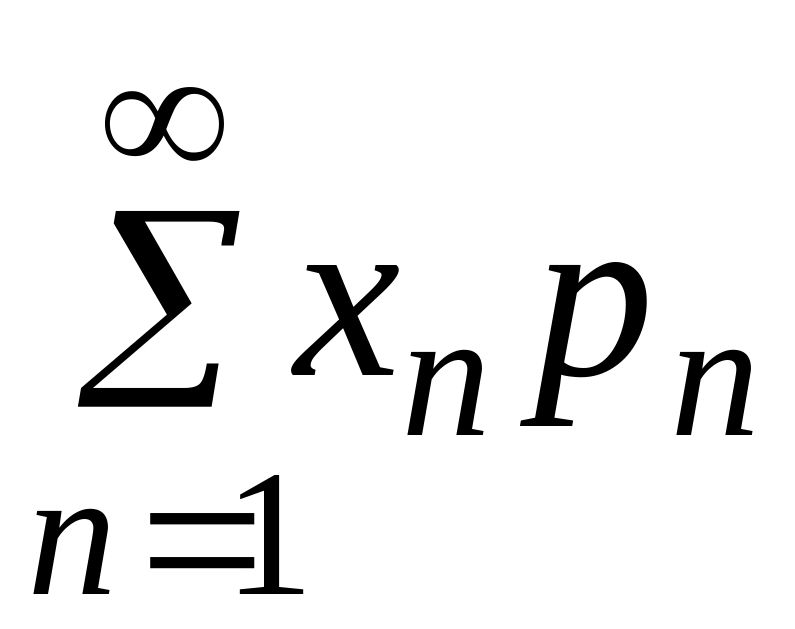16. Дискретная случайная величина имеет закон распределения

	0	1	2
р	0,3	0,5	0,2

Найти дисперсию и среднее квадратическое отклонение случайной величины .

Решение. Дисперсию вычислим по формуле

Найдем для этого математическое ожидание квадрата случайной величины :

Тогда

В соответствии с формулой находим среднее квадратическое отклонение

0. 17. Случайная величина задана плотностью вероятности:

1. 

Найти математическое ожидание и дисперсию случайной величины .

Решение. Найдем математическое ожидание и дисперсию случайной величины по формулам:

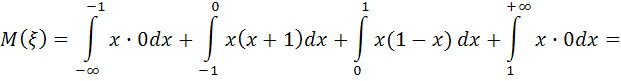
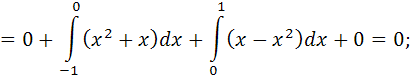
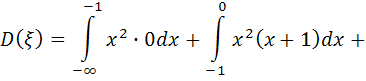
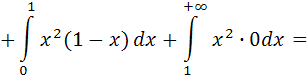
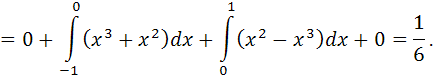
18. Случайная величина распределена по нормальному закону, причем его параметры равны: т=10, =2. Найти .

Решение.

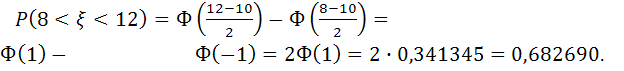
19. Для случайной величины известна дисперсия и неравенство Найти число а.

Решение. Согласно первому неравенству Чебышева

получаем

Из этих неравенств следует, что

откуда

Следовательно,

20. Для случайной величины известна дисперсия и

неравенство Найти значение .

Решение. Согласно второму неравенству Чебышева получаем По условию . Из этих двух равенств следует, что

Задачи по «Математической статистике»

21. Выборка задана простым статистическим рядом:

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
хi	10	15	10	7	5	15	10	10	7	15	10	5	15	10	7	15	10	15	15	10

Задания:

а) Составить точечный статистический ряд. Построить полигон. Найти статистическую функцию распределения, выборочную среднюю и выборочную дисперсию.

b) Составить интервальный статистический ряд, взяв отрезок [4;16] и длину разбиения h=2. Построить гистограмму. Найти выборочную среднюю и выборочную дисперсию.

Решение.

а) 1. Точечный статистический ряд:

xi	5	7	10	15
mi	2	3	8	7

(n=2+3+8+7=20).

2. Полигон:

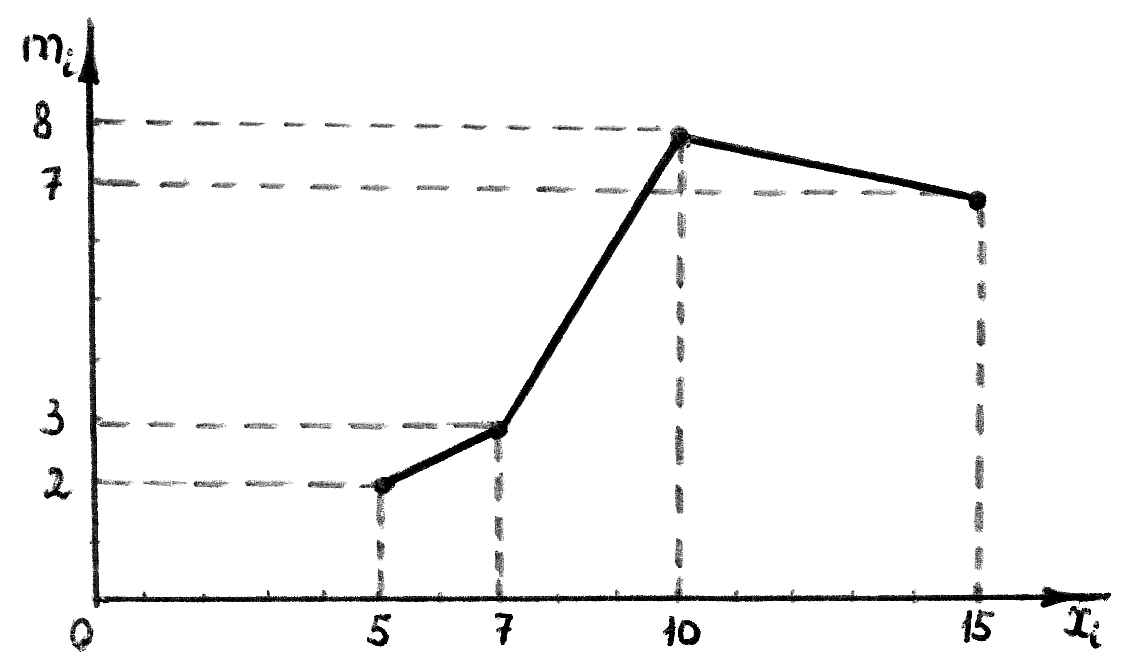
3. Статистическая функция распределения:

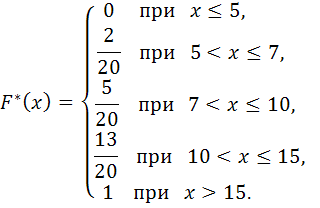
4. Выборочная средняя:

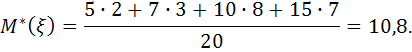
5. Выборочная дисперсия:

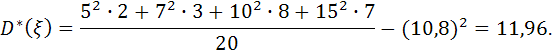
6. Выборочное среднее квадратическое отклонение:

b) 1. Интервальный статистический ряд:

hi	[4;6]	[6;8]	[8;10]	[10;12]	[12;14]	[14;16]
ki	2	3	4	4	0	7

2. Гистограмма:

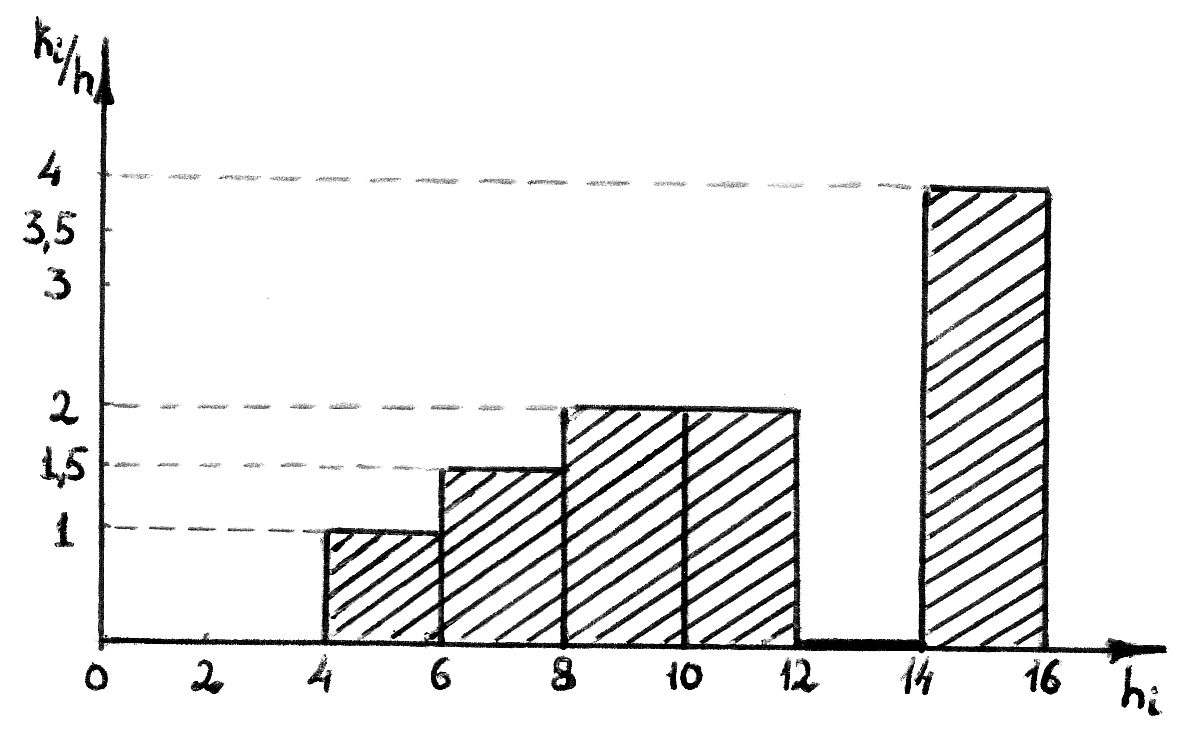
3. Выборочная средняя:

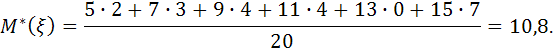
4. Выборочная дисперсия:

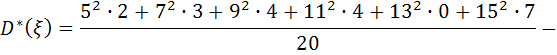
22. Случайная величина распределена по показательному закону. Статистическое распределение выборки представлено в таблице:

xi	5	15	25	35	45	55	65
mi	365	245	150	100	70	45	25

Найти точечную оценку параметра методом наибольшего правдоподобия.

Решение. 1) Составим функцию правдоподобия:

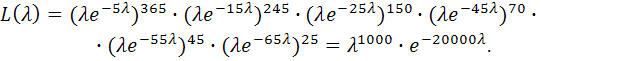
2) Решим уравнение

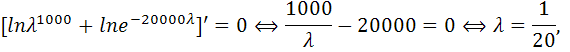
23. Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания нормально распределенной случайной величины , если известны ее среднее квадратическое отклонение , выборочная средняя и объем выборки n=16.

Решение. По надежности из соотношения находим значение функции Лапласа: Ф(z)=0,475.

По таблице значений функции Лапласа (см. Таблицу 2) находим z=1,96. Используя неравенства для интервальной оценки математического ожидания, получаем

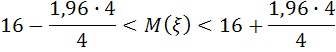
или

24. По данным выборки объема n=25 найдено несмещенное значение выборочного среднего квадратического отклонения нормально распределенной случайной величины . Найти с надежностью 0,99 доверительный интервал для оценки среднего квадратического отклонения случайной величины.

Решение. На основании данных значений , n=25 по таблице (см. Таблицу 3) находим значение q=0,49. Подставляем в неравенства

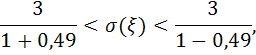
откуда

25. Результаты взвешивания 50 случайным образом отобранных пачек чая приведены ниже (в граммах):

150, 147, 152, 148, 149, 153, 151, 149, 147, 153, 151, 152, 151, 149, 152, 150, 148, 152, 150, 152, 151, 148, 151, 152, 150, 151, 149, 148, 149, 150, 150, 151, 149, 151, 150, 151, 150, 149, 148, 147, 153, 147, 152, 150, 151, 149, 150, 151, 153.

Оценить закон распределения случайной величины - массы пачки чая – для уровня значимости

Решение. Масса пачки чая – непрерывная случайная величина, но в силу того, что взвешивание проведено с дискретностью 1 г и размах составляет 147 – 153 г, непрерывная величина может быть представлена точечным статистическим рядом:

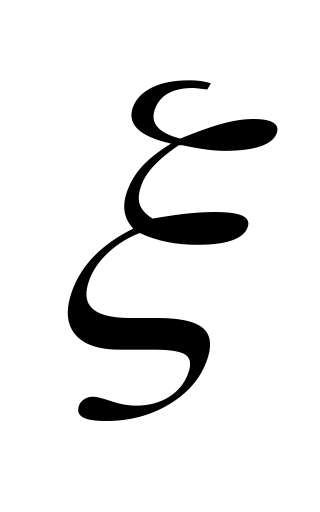
Значение случайной величины	xi	147	148	149	150	151	152	153
Частота появления	mi	4	5	8	11	11	7	4

В качестве модели закона распределения выберем нормальный закон , число параметров которого r=2: – математическое ожидание, - среднее квадратическое отклонение.

По выборочным данным получим оценки параметров нормального закона распределения:

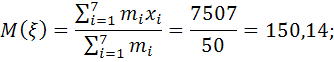
Для расчета теоретических частот воспользуемся табличными значениями функции Лапласа Ф(z). Алгоритм вычисления состоит в следующем:

• находим по нормированным значениям случайной величины 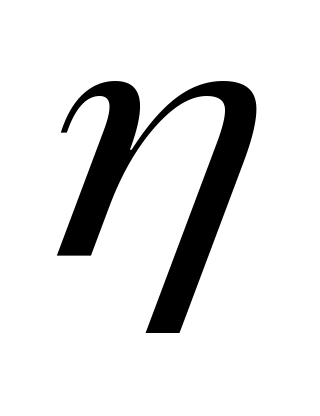значения Ф(z), а затем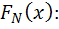

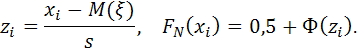
Например,

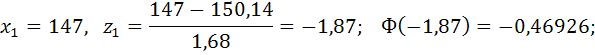
• находим

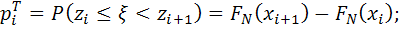
• находим 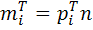и если некоторое 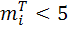, то соответствующие группы объединяются.

Результаты вычисления , и приведены в таблице.

По таблице (см. приложение 4) находим по схеме: для уровня значимости и числа степеней свободы

Следовательно, критическая область (7,8; ).

Величина 5,267 не входит в критическую область, поэтому гипотеза о том, что случайная величина - масса пачки чая – подчинена нормальному закону распределения, согласуется с выборочными данными.

Таблица

i	xi-xi+1	mi	Ф(zi)			=
0	- -147	0	-0,50000	0,00000	0,03074	0,03074	1,537	-
1	147-148	4	-0,46926	0,03074	0,10204	0,07130	3,563	0,237
2	148-149	5	-0,39796	0,10204	0,24825	0,14621	7,31	0,730
3	149-150	8	-0,25175	0,24825	0,46812	0,21987	10,99	0,813
4	150-151	11	-0,03188	0,46812	0,69497	0,22685	11,34	0,010
5	151-152	11	0,19497	0,69497	0,86650	0,17153	8,58	0,683
6	152-153	7	0,36650	0,86650	0,95543	0,08893	4,45	2,794
7	153-	4	0,45543	0,95543	1,00000	0,04457	2,23	-