Додаток б Взірець виконання розрахункової роботи
1Основні теоретичні відомості
Будь-яка динамічна або статична система характеризується своїм станом в певний момент часу. Поняття стану системи в момент часу t0 включає в себе інформацію яка разом з деякою вхідною функцією заданою для t >t0 адекватно визначає єдину вихідну функцію для t >t0 .
Стан описується n - мірним вектором стану:
,
компонентами якого є змінні стану. Система для опису якої необхідно n - змінних стану називається системою n-го порядку.
Існують системи для опису яких необхідна нескінченна множина змінних стану (наприклад лінія затримки). Про такі системи говорять що вони мають нескінченно-мірний простір стану. Якщо система допускає представлення з допомогою простору стану і описується звичайними диференційними рівняннями то її можна описати сукупністю рівнянь:
(1.1)
де - вектор змінної стану, - вектор вхідної дії, - вектор виходу системи, - вектор початкового стану системи. Такий опис системи називається рівнянням стану у стандартній формі. Перше диференційне рівняння називається рівнянням стану, а друге рівнянням вхід-стан-вихід.
Існують деякі специфічні стани:
Нульовий стан – це деякий стан для якого виконується умова 0=g(,0,t);
Встановлений стан – це такий стан в який система приходить при нульовій вхідній дії незалежно від початкового стану;
Стан рівноваги – це деякий стан при якому система залишається сталою тобто виконується умова f(,0,t)=0 або x(t)=const.
Основною характеристикою систем є їх реакція на нульову вхідну дію та на нульовий початковий стан.
Якщо вхідна дія є нульовою а реакція системи відмінна від нуля то вона є єдино можливою для даного початкового стану (початкового запасу енергії) і називається реакцією на нульову вхідну дію.
Реакція системи на довільну вхідну дію при нульовому початковому стані називається реакцією на нульовий початковий стан.
Система володіє властивістю декомпозиції якщо виконується наступна умова: якщо є реакцією на нульову вхідну дію при довільному початковому стані, а – реакцією на нульовий початковий стан для довільної вхідної дії то реакція на той же початковий стан і ту ж вхідну дію буде: .
Якщо система лінійна відносно нульового початкового стану та лінійна відносно нульової вхідної дії а також володіє властивістю декомпозиції то вона називається лінійною. Аналогічно визначається лінійність відносно співвідношення – вхід – стан – вихід. Аналогічно визначається лінійність і по змінній стану. Тобто для лінійних систем загальна зміна стану описується співвідношенням
.
Слід виділити властивість стаціонарності. Стаціонарність – це незалежність характеристик системи від часу початку її еволюції.
Для випадку лінійних систем рівняння стану у стандартній формі (1.1) має вигляд
(1.2)
де
- функціональні матриці відповідних
розмірностей. Для лінійних систем
важливим поняттям є перехідна
матриця стану
,
яка відповідає оператору відображення
початкового стану
у текучій стан
при нульовій вхідній дії:
.
(1.3)
Розв’язком рівнянь (1.2) з врахуванням (1.3) будуть наступні вирази:
- реакція стану на нульовий вхідний вплив:
;
(1.4)
- реакція стану на нульовий початковий стан:
;
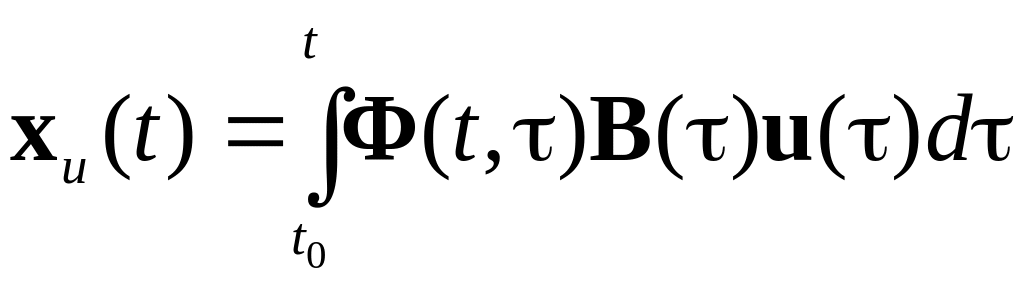(1.5)
- реакція стану на заданий початковий стан і заданий вхідний вплив :
;
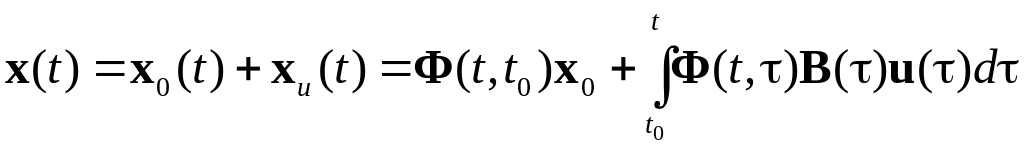(1.6)
- реакція системи на нульовий вхідний вплив:
;
(1.7)
- реакція системи на нульовий початковий стан:
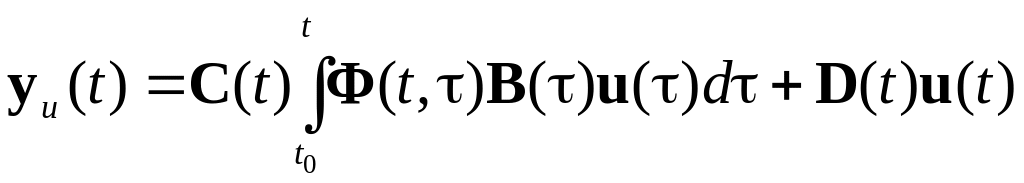; (1.8)
- реакція системи на заданий початковий стан і заданий вхідний вплив :
. (1.9)
Для випадку стаціонарних систем матриці у виразі (1.2) будуть числовими і відповідне рівняння стану у стандартній формі буде мати вигляд:
(1.10)
а перехідна матриця стану має вигляд:
(1.11)
Підставивши (1.11) у вирази (1.4) – (1.9) можна отримати відповідні вирази розв’язку (1.10):
; (1.12)
; (1.13)
; (1.14)
; (1.15)
; (1.16)
. (1.17)
Отримавши розв’язок диференційного рівняння який характеризує стан системи в будь-який момент часу, можна дослідити всі динамічні характеристики системи.
Для спрощення розрахунків і надання можливості цифрової обробки даних широкого застосування на практиці отримали методи апроксимації неперервних систем системами з дискретним часом. Такі системи отримуються шляхом здійснення вибірки і затримки вхідної функції і вибірки значень і в дискретні моменти часу , де інтервал дискретизації.
На основі процедури вибірки рівняння стану у стандартній формі, неперервної лінійної стаціонарної системи, може бути апроксимоване різницевими рівняннями у систему з дискретним часом, яка описується дискретним рівняннями стану:
(1.18)
де
(1.19)
дискретна перехідна матриця стану,
(1.20)
- аналог матриці у (1.10), а - інтервал дискретизації вибірки.
2ЗАВДАННЯ ДО РОЗРАХУНКОВОЇ РОБОТИ
Зміст першої частини роботи: ”Дослідження характеристик динамічної системи третього порядку з неперервним часом”
2.1.1Побудувати математичну модель заданої динамічної системи використовуючи основні природні закони (закони Кіргофа) з кінцевим представленням у вигляді рівняння стану у стандартній формі. У якості виходу системи взяти падіння напруги на активних опорах.
2.1.2Визначити перехідну матрицю стану, отриманого рівняння.
2.1.3Визначити реакцію стану системи на нульовий вхідний вплив з представленням результатів у вигляді графічної залежності.
2.1.4Визначити реакцію стану системи на нульовий початковий стан з представленням результатів у вигляді графічної залежності.
2.1.5Визначити реакцію системи на нульовий вхідний вплив з представленням результатів у вигляді графічної залежності.
2.1.6Визначити реакцію системи на нульовий початковий стан з представленням результатів у вигляді графічної залежності.
2.1.7Визначити загальну реакцію системи з представленням результатів у вигляді графічної залежності.
2.1.8Привести рівняння стану у стандартній формі до канонічного виду у просторі власних векторів.
Зміст другої частини роботи : ”Дослідження характеристик динамічної системи високого порядку з дискретним часом ”
2.1.9Побудувати математичну модель заданої динамічної системи з представленням у вигляді дискретного рівняння стану у стандартній формі.
2.1.10Визначити дискретну перехідну матрицю стану, отриманого рівняння.
2.1.11Визначити реакцію системи на нульовий вхідний вплив з представленням результатів у вигляді графічної залежності.
2.1.12Визначити реакцію системи на нульовий початковий стан з представленням результатів у вигляді графічної залежності.
2.1.13Визначити загальну реакцію системи з представленням результатів у вигляді графічної залежності
2.1.14Зробити порівняльний аналіз отриманих результатів у випадках аналогового і дискретного представлення системи.
Зміст третьої частини роботи : ”Аналіз результатів моделювання на не протиріччя
2.1.15Перетворити вихідну схему до еквівалентної схеми при встановленому значенні вхідного впливу.
2.1.16Визначити встановлені значення входу і виходу і стану системи при .
2.1.17Порівняти отримані встановлені значення з графічними результатами моделювання.
Варіант № 0
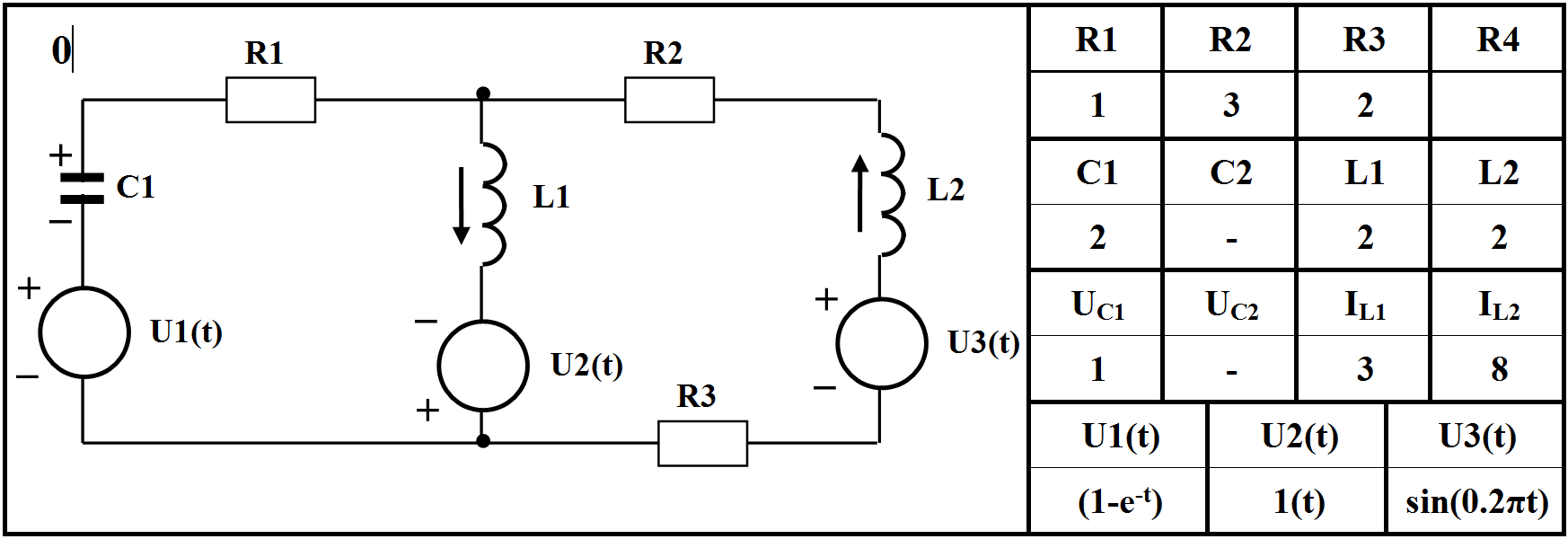
Рисунок 1.1 – Схема системи та значення параметрів і характеристик
4 ДОСЛІДЖЕННЯ ЛІНЙНОЇ ДИНАМІЧНОЇ СИСТЕМИ З НЕПЕРЕРВНИМ ЧАСОМ