МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Івано-Франківський національний технічний

університет нафти і газу

Кафедра комп’ютерних технологій в системах управління і автоматики

О.Г.Малько

СПЕЦІАЛЬНІ РОЗДІЛИ МАТЕМАТИКИ

Методичні вказівки до виконання

розрахункової роботи:

«Дослідження динамічних систем високого порядку з неперервним і дискретним часом»

Для підготовки бакалаврів за напрямком

6.050201 – “Системна інженерія”

Рекомендовано методичною радою університету.

Івано-Франківськ

2010

МВ 02070855 – 3066 – 2010

Малько О.Г. Спеціальні розділи математики: Методичні вказівки до виконання розрахункової роботи. Івано-Франківськ: ІФНТУНГ, 2010. – 322 с.

Методичні вказівки складені згідно з програмою курсу “Спеціальні розділи математики”.

Виконання розрахункової роботи на тему «Дослідження динамічних систем високого порядку з неперервним і дискретним часом» направлене на отримання практичних навичок моделювання систем високого порядку у ракурсі: побудови математичної моделі системи у вигляді рівняння стану у стандартній формі, дослідження отриманої моделі з неперервним і дискретним часом у середовищі MathCAD, аналіз результатів моделювання на не протиріччя, виходячи з математичних і фізичних аспектів.

Призначено для підготовки бакалаврів за напрямком 6.050201 – “Системна інженерія”.

Рецензент: канд. техн. наук, доцент кафедри “Комп’ютерних технологій в системах управління та автоматики” Олійник А.П.

© Малько О.Г., 2010

© ІФНТУНГ, 2010

ЗМІСТ

1 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ 4

2 ЗАВДАННЯ ДО РОЗРАХУНКОВОЇ РОБОТИ ЇЇ ОФОРМЛЕННЯ ТА ЗМІСТ 8

Завдання до розрахункової роботи її оформлення 8

СПИСОК РЕКОМЕНДОВАНИХ ДЖЕРЕЛ 10

ДОДАТОК Б Взірець виконання розрахункової роботи 11

1 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ 13

2 ЗАВДАННЯ ДО РОЗРАХУНКОВОЇ РОБОТИ 17

4 ДОСЛІДЖЕННЯ ЛІНЙНОЇ ДИНАМІЧНОЇ СИСТЕМИ З НЕПЕРЕРВНИМ ЧАСОМ 21

5 ДОСЛІДЖЕННЯ ЛІНЙНОЇ ДИНАМІЧНОЇ СИСТЕМИ З ДИСКРЕТНИМ ЧАСОМ 25

6 АНАЛІЗ РЕЗУЛЬТАТІВ МОДЕЛЮВАННЯ НА НЕ ПРОТИРІЧЧЯ 28

1Короткі теоретичні відомості

Будь-яка динамічна або статична система характеризується своїм станом в певний момент часу. Поняття стану системи в момент часу t₀ включає в себе інформацію яка разом з деякою вхідною функцією заданою для t >t₀ адекватно визначає єдину вихідну функцію для t >t₀ .

Стан описується n - мірним вектором стану:

,

компонентами якого є змінні стану. Система для опису якої необхідно n - змінних стану називається системою n-го порядку.

Існують системи для опису яких необхідна нескінченна множина змінних стану (наприклад лінія затримки). Про такі системи говорять що вони мають нескінченно-мірний простір стану. Якщо система допускає представлення з допомогою простору стану і описується звичайними диференційними рівняннями то її можна описати сукупністю рівнянь:

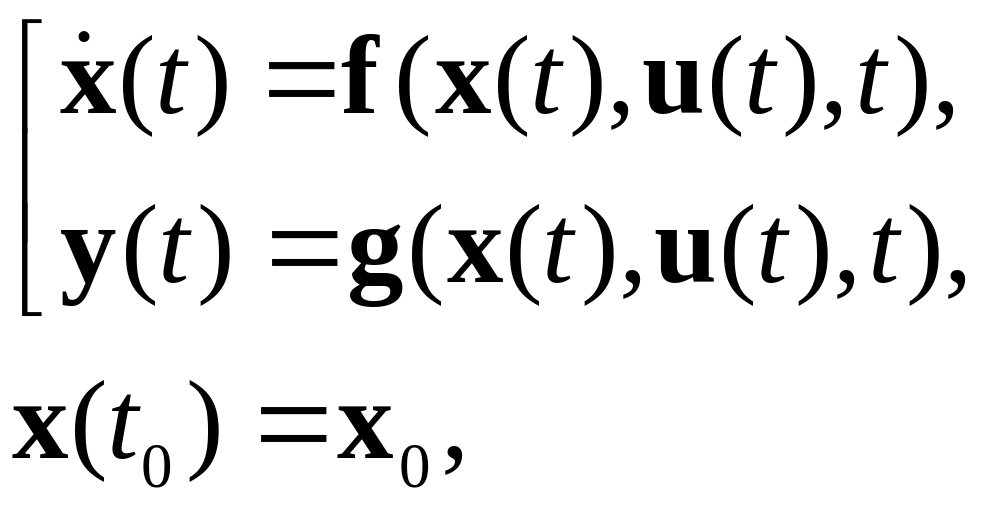(1.1)

де - вектор змінної стану, - вектор вхідної дії, - вектор виходу системи, - вектор початкового стану системи. Такий опис системи називається рівнянням стану у стандартній формі. Перше диференційне рівняння називається рівнянням стану, а друге рівнянням вхід-стан-вихід.

Існують деякі специфічні стани:

Нульовий стан – це деякий стан  для якого виконується умова 0=g(,0,t);

Встановлений стан – це такий стан  в який система приходить при нульовій вхідній дії незалежно від початкового стану;

Стан рівноваги – це деякий стан  при якому система залишається сталою тобто виконується умова f(,0,t)=0 або x(t)=const.

Основною характеристикою систем є їх реакція на нульову вхідну дію та на нульовий початковий стан.

Якщо вхідна дія є нульовою а реакція системи відмінна від нуля то вона є єдино можливою для даного початкового стану (початкового запасу енергії) і називається реакцією на нульову вхідну дію.

Реакція системи на довільну вхідну дію при нульовому початковому стані називається реакцією на нульовий початковий стан.

Система володіє властивістю декомпозиції якщо виконується наступна умова: якщо є реакцією на нульову вхідну дію при довільному початковому стані, а – реакцією на нульовий початковий стан для довільної вхідної дії то реакція на той же початковий стан і ту ж вхідну дію буде: .

Якщо система лінійна відносно нульового початкового стану та лінійна відносно нульової вхідної дії а також володіє властивістю декомпозиції то вона називається лінійною. Аналогічно визначається лінійність відносно співвідношення – вхід – стан – вихід. Аналогічно визначається лінійність і по змінній стану. Тобто для лінійних систем загальна зміна стану описується співвідношенням

.

Слід виділити властивість стаціонарності. Стаціонарність – це незалежність характеристик системи від часу початку її еволюції.

Для випадку лінійних систем рівняння стану у стандартній формі (1.1) має вигляд

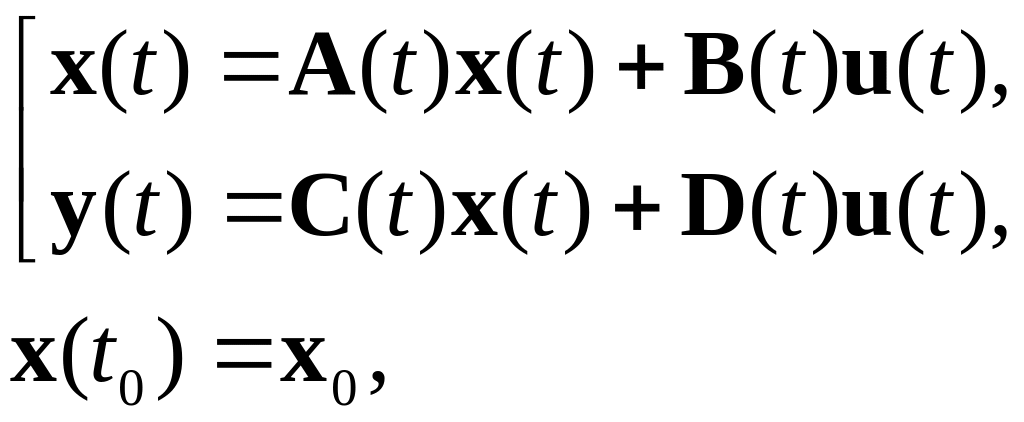(1.2)

де - функціональні матриці відповідних розмірностей. Для лінійних систем важливим поняттям є перехідна матриця стану , яка відповідає оператору відображення початкового стану у текучій стан при нульовій вхідній дії:

. (1.3)

Розв’язком рівнянь (1.2) з врахуванням (1.3) будуть наступні вирази:

- реакція стану на нульовий вхідний вплив:

; (1.4)

- реакція стану на нульовий початковий стан:

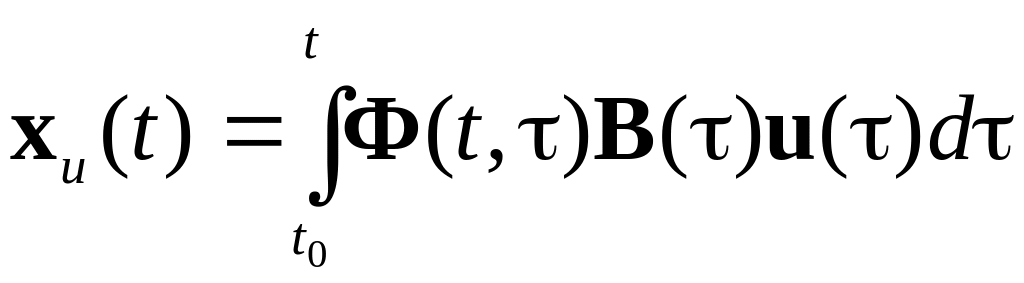; (1.5)

- реакція стану на заданий початковий стан і заданий вхідний вплив :

; (1.6)

- реакція системи на нульовий вхідний вплив:

; (1.7)

- реакція системи на нульовий початковий стан:

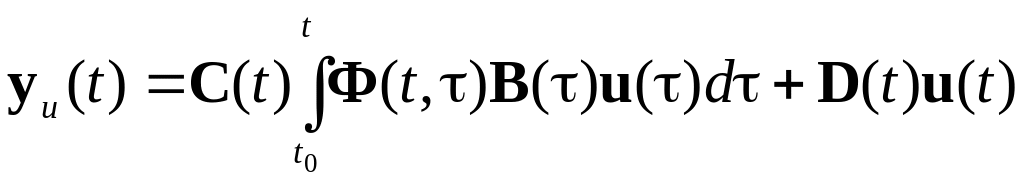; (1.8)

- реакція системи на заданий початковий стан і заданий вхідний вплив :

. (1.9)

Для випадку стаціонарних систем матриці у виразі (1.2) будуть числовими і відповідне рівняння стану у стандартній формі буде мати вигляд:

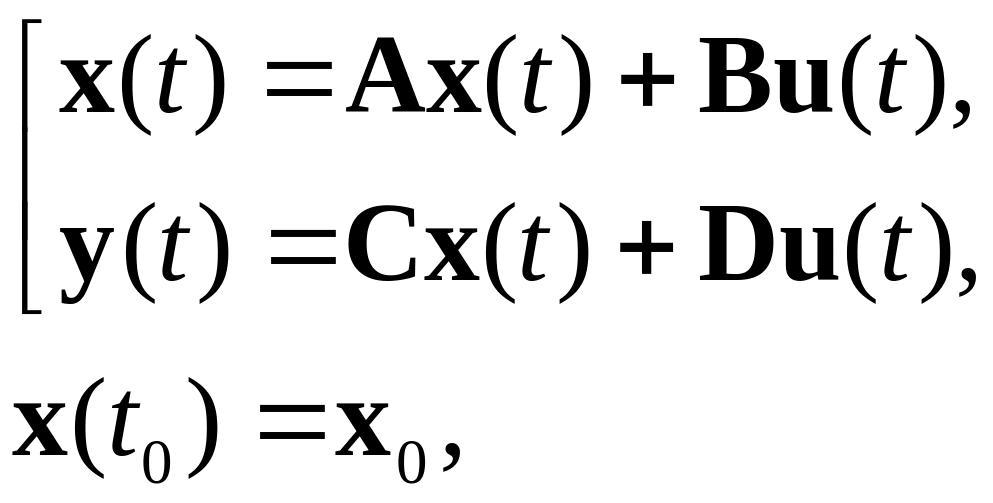(1.10)

а перехідна матриця стану має вигляд:

(1.11)

Підставивши (1.11) у вирази (1.4) – (1.9) можна отримати відповідні вирази розв’язку (1.10):

; (1.12)

; (1.13)

; (1.14)

; (1.15)

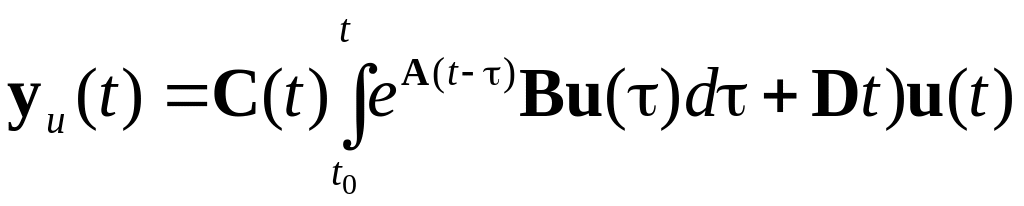; (1.16)

. (1.17)

Отримавши розв’язок диференційного рівняння який характеризує стан системи в будь-який момент часу, можна дослідити всі динамічні характеристики системи.

Для спрощення розрахунків і надання можливості цифрової обробки даних широкого застосування на практиці отримали методи апроксимації неперервних систем системами з дискретним часом. Такі системи отримуються шляхом здійснення вибірки і затримки вхідної функції і вибірки значень і в дискретні моменти часу , де інтервал дискретизації.

На основі процедури вибірки рівняння стану у стандартній формі, неперервної лінійної стаціонарної системи, може бути апроксимоване різницевими рівняннями у систему з дискретним часом, яка описується дискретним рівняннями стану:

(1.18)

де

(1.19)

- дискретна перехідна матриця стану,

(1.20)

- аналог матриці у (1.10), а - інтервал дискретизації вибірки.

При виборі кроку чисельного інтегрування виходити з умови мінімального значення сталої часу експонент:

,

або мінімального значення сталої часу гармонійних складових максимуму

,

де - характеристичні числа матриці .

Інтервал дискретизації по часу повинен задовольняти умовам

,

Інтервал інтегрування вибирається за умовою

.