1.14 Интерполяционная формула Уиттекера

Интерполяционная формула Уиттекера — Шеннона служит для восстановления непрерывного сигнала с ограниченным спектром из последовательности равноотстоящих отсчётов.

Интерполяционная формула, как её обычно называют, восходит к работе Эмиля Бореля, датированной 1898 годом, и к работе Эдмунда Уиттекера, датированной 1915 годом. Интерполяционная формула была процитирована из работы сына Эдмунда Уиттекера — Джона Макнагтена Уиттекера, датированной 1935 годом, в виде теоремы отсчётов Найквиста — Шеннона в 1949 году, автором редакции был Клод Шеннон, до Шеннона данную теорему сформулировал Котельников. Также интерполяционную формулу обычно называют интерполяционной формулой Шеннона, или интерполяционной формулой Уиттекера.

Теорема отсчётов гласит, что при некоторых ограничивающих условиях, функция   может быть восстановлена из её дискретизации,  , согласно интерполяционной формуле Уиттекера — Шеннона:

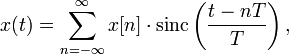где   — период дискретизации,   — частота дискретизации,   — нормализированная sinc-функция.

С двух сторон пропускная способность   известна как частота Найквиста для сигнала.

Есть два граничных условия, которым должна удовлетворить функция  , для того чтобы выполнялась интерполяционная формула:

 должно быть ограничено. Преобразование Фурье для функции   должно обладать следующим свойством:   для  , где  .

Частота дискретизации   должна в два раза превышать диапазон частот,  , или что эквивалентно:

где   — период дискретизации.

Интерполяционная формула воссоздаёт оригинальный сигнал  , только тогда, когда эти два условия будут выполнены. В противном случае возникает наложение высокочастотных компонентов на низкочастотные —алиасинг.

1.15 Амплитудная модуляция

Под амплитудной модуляцией сигнала понимается модификация высокочастотного сигнала в соответствие с изменением амплитуды модулирующего сигнала. Частотный спектр рассматриваемого модулирующего сигнала имеет границы в соответствие с временной полосой частот. Если мы воздействуем на амплитудную модуляцию дискретными сигналами, то изменение амплитуды будет зависеть от заложенных уровней булевых 0 и 1. Т.е. наш сигнал будет модулироваться импульсами, где частотный спектр в полнее велик.

Отсюда можно сделать выводы, что чем у нас больше частота нашего несущего сигнала, тем и модулирующий сигнал можно передать более широкополосным (пропускная способность увеличивается). Так же для ее увеличения можно прибегнуть к увеличению уровней модуляции, но данный способ плох низкой помехоустойчивостью.

Амплиту́дная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда

Первый опыт передачи речи и музыки по радио методом амплитудной модуляции произвёл в 1906 году американский инженер Р. Фессенден. Несущая частота 50 кГц радиопередатчика вырабатывалась машинным генератором (альтернатором), для её модуляции между генератором и антенной включался угольный микрофон, изменяющий затухание сигнала в цепи. С 1920 года вместо альтернаторов стали использоваться генераторы на электронных лампах. Во второй половине 1930-х годов, по мере освоения ультракоротких волн, амплитудная модуляция постепенно начала вытесняться из радиовещания и радиосвязи на УКВ частотной модуляцией. С середины XX века в служебной и любительской радиосвязи на всех частотах внедряется модуляция с одной боковой полосой (ОБП), которая имеет ряд важных преимуществ перед АМ. Поднимался вопрос о переводе на ОБП и радиовещания, однако это потребовало бы замены всех радиовещательных приёмников на более сложные и дорогие, поэтому не было осуществлено. В конце XX века начался переход к цифровому радиовещанию с использованием сигналов с амплитудной манипуляцией.

Аудиосигнал может модулировать амплитуду (AM) или частоту (ЧМ) несущей.

Пусть  — информационный сигнал,  ,  — несущее колебание.

Т огда амплитудно-модулированный сигнал   может быть записан следующим образом:

З десь   — некоторая константа, называемая коэффициентом модуляции. Формула (1) описывает несущий сигнал  , модулированный по амплитуде сигналом   с коэффициентом модуляции  . Предполагается также, что выполнены условия:

В ыполнение условий (2) необходимо для того, чтобы выражение в квадратных скобках в (1) всегда было положительным. Если оно может принимать отрицательные значения в какой-то момент времени, то происходит так называемая перемодуляция (избыточная модуляция). Простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями.