Метод хорд

 Пример

Дано уравнение х³ – 0,2x² + 0,5x + 1,5 = 0. Уточнить корень с погрешностью  < 0,001.

 Решение

Запишем f(х) = х³ – 0,2x² + 0,5x + 1,5.

Проведя процедуру отделения корней, получим, что корень находится в промежутке [-1; 0], т. е. а = -1; Ь = 0.

f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2 < 0;

f(0) = 1,5 > 0.

Находим вторую производную f"(х) = 6х – 0,4.

f"(-1) = -6 – 0,4 = -6,4 < 0;

f"(0) = -0,4 = -0,4 < 0.

На конце а отрезка [а,b] выполняется условие f(-1) f"(-1) > 0, поэтому для вычислений применяем формулу:

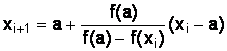,                                          (3.1)

где x₀ = b; f(a) = f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2.

Все вычисления сведены в табл. 3.5.

Таблица 3.5 

Результаты расчетов по методу хорд

i	xi	f(xi)	xi-a
0	0	1,5	1
1	-0,882	0,2173	0,118
2	-0,943	0,0121	0,057
3	-0,946	0,0014	0,054
4	-0,946

Ответ: х-0,946. 

Метод Ньютона

 Пример

Дано уравнение: х³ – 0,2x² + 0,5x + 1,5 = 0. Уточнить корень с погрешностью  < 0,001.

 Решение

Запишем f(х) =х³ – 0,2x² + 0,5x + 1,5.

Проведя процедуру отделения корней, получим, что корень находится в промежутке [-1; 0], т. е. а = -1, Ь = 0.

f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2 < 0;

f(0) = 1,5 > 0.

Находим первую производную: f'(х) = 3х² – 0,4x + 0,5.

Находим вторую производную: f"(х) = 6х – 0,4.

f"(-1) = -6 – 0,4 = -6,4 < 0;

f"(0) = – 0,4 = -0,4 < 0.

На конце а отрезка [а,b] выполняется условие f(-1) f"(-1) > 0, поэтому за начальное приближение примем x₀ =0,8, а вычисления будем проводить по формуле

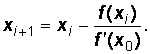                                                  (3.2)

 

Предварительно найдем f'(х₀) = 3 (-1)² – 0,4 (-1) + 0,5 = 3,9.

Составим таблицу расчетов (табл. 3.6).

Таблица 3.6

Результаты расчетов по методу Ньютона

i	xi	f(xi)
0	-1	-0,2000
1	-0,9487	-0,0083
2	-0,9466	-0,0007
3	-0,9464	-0,0001

Ответ: x-0,9464.

Метод простой итерации

 Пример

Имеем уравнение 2х + lg(2x + 3) = 1. Необходимо уточнить корень с погрешностью   < 0,001.

 Решение

Запишем f(х) = 2х + lg(2x +3) – 1. Проведя процедуру отделения корней, получим, что корень находится в промежутке [0;0,5], т. е. а = 0, Ь =0,5.

Приведем уравнение f(х)=0 к виду, удобному для итераций: (х) = х. Для этого уравнение 2х + lg(2x +3) –1=0 выразим следующим образом:

(х) = х= 0,5 – 0,5 lg(2x +3).

Найдем первую производную функции '(x):

'(x )= -0,5·lg(е)/(2х+3)·2 = – lg(е)/(2х+3); lg(е)  0,4343;

'(0 )= -lg(е)/(2·0+3) = – 0,1448; '(0,5)= -lg(е)/(2·0,5+3)= – 0,1086.

Следовательно, на отрезке [0;0,5] |'(х)|  1 и к уравнению можно применить метод итерации.

За начальное приближение возьмем х₀ =0, все остальные прибли­же­ния будем определять из равенства: х_i+1 = 0,5 – 0,5 lg(2x_i +3), резуль­та­ты све­дем в табл. 3.8.

Таблица 3.8 

Результаты расчетов по методу итерации

i	xi	(х) = хi+1
0	0	0,2614
1	0,2614	0,2266
2	0,2266	0,2309
3	0,2309	0,2303
4	0,2303	0,2304
5	0,2304

Ответ: х  0,230.