3.Выводы

Задача отыскания корней нелинейного уравнения вида , где  — непрерывная на отрезке  функция, не теряет актуальности и в наши дни, хотя имеет многовековую историю. Она может быть использована при решении важных научных и технических проблем. Существует много методов, позволяющих достаточно быстро находить приближённое значение корня с требуемой точностью. Сравнительный анализ методов поиска решений нелинейных уравнений позволяет сделать следующие выводы.

Самый надёжный метод – это метод половинного деления отрезка локализации корня, который не требует существования производной данной функции. Особое место среди методов решения нелинейных уравнений занимает метод Ньютона, или метод касательных. Однако при его практическом применении можно столкнуться с некоторыми трудностями. Одна из них состоит в необходимости вычисления первой и второй производных функции . Более существенно то, что метод Ньютона обладает только так называемой локальной сходимостью. Это означает, что для гарантии сходимости необходимо выбирать хорошее начальное приближение, в противном случае неудачный выбор отрезка локализации корня может дать расходящуюся последовательность.

Эти методы являются чисто математическими и не привлекают физических соображений к поиску возможного пересечения функции с осью абсцисс.

4. Приложение Отделение корней

 Пример 1. Дано уравнение: 5^х–6х–3 = 0. Найти количество корней и интервалы нахождения этих корней.

 Решение

Обозначим: f(х) = 5^х–6х–3. Находим производную: f'(x) = 5^х ln5–6. Вычислим корень производной:

5^х ln5 – 6 = 0; 5^х = 6/ln5;  xlg5 = lg6–lg(ln5);

х = (lg6–lg(ln5))/lg5 = (0,7782 – 0,2065)/0,6990 = 0,5717/0,69900,82.

Составим таблицу (табл. 3.1) знаков функции f(х), полагая х, равным:

а) критическим значениям функции (корням производной) или близким к ним;

б) граничным значениям (исходя из области допустимых значений неизвестного).

Таблица 3.1

Таблица знаков функции

х	-	1	+
sign f(x)	+	–	+

Так как происходят две перемены знака функции, то уравнение имеет два действительных корня. Чтобы завершить операцию отделения корней, можно попытаться уменьшить промежутки, содержащие корни, таким образом, чтобы их длина была меньше. Для этого возьмем несколько значений х и внесем их дополнительно в табл. 3.2.

Таблица 3.2

Дополнительная таблица знаков функции

х	-	-1	0	1	2	+
sign f(x)	+	+	-	-	+	+

 Отсюда видно, что корни заключены в следующих промежутках:

x₁[-1,0]; x₂[1,2].

Примечание. Отделить корни можно и графически. Для этого строится график функции, и по графику определяется интервал, на котором находится корень (точка пересечения графика с осью х).

 Пример 2. Дано уравнение: 5^х – 6х – 3 = 0.

 Решение

Обозначим: У = 5^х – 6х – 3.

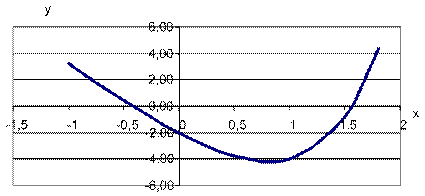
На интервале [-1;1,8] необходимо вычислить значения функции У. Результаты расчета занести в таблицу 2.3 и построить график этой функции. График функции: У = 5^{х –} 6х – 3 представлен на рис. 3.1.

Таблица 3.3

Расчет значений функции У

х	-1	-0,5	0	0,5	1	1,5	1,8
Y	3,20	0,45	-2,00	-3,76	-4,00	-0,82	4,32

(рис.3.1)

 

Рис. 3.1. График функции: У = 5^х – 6х – 3

По графику определяем, что корни заключены в следующих промежутках: x₁[-1;0]; x₂[1;1,8].

Метод деления отрезка пополам:

 Пример

Дано уравнение: х³ – 0,2x² + 0,5x + 1,5 = 0. Уточнить корень с погрешностью  < 0,001.

 Решение

Запишем: f(х) = х³ – 0,2x² + 0,5x + 1,5.

Проведя процедуру отделения корней, получим, что корень находится в промежутке [-1; 0], т.е. а = -1, Ь = 0.

f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2 < 0;

f(0) = 1,5 > 0.

Делим интервал [-1; 0] на две части, т.е. находим х = (-1+0)/2 = -0,5. Затем определяем произведение f(a)·f(x). Если f(a)·f(x)>0, то начало интервала a переносим в точку х (а=х). Если f(a)·f(x)<0, то конец интервала b переносим в точку х (b=х). Затем новый интервал делим пополам и т.д. Результаты расчетов представлены в табл. 3.4.

Таблица 3.4

Результаты расчетов по методу деления отрезка пополам

a	b	x	f(a)	f(x)	f(a) f(x)
-1,0000	0,000000	-0,50000	-0,2000	1,0750	-0,2150000
-1,0000	-0,500000	-0,75000	-0,2000	0,5906	-0,1181250
-1,0000	-0,750000	-0,87500	-0,2000	0,2395	-0,0478906
-1,0000	-0,875000	-0,93750	-0,2000	0,0315	-0,0062988
-1,0000	-0,937500	-0,96875	-0,2000	-0,0812	0,0162439
-0,9688	-0,937500	-0,95313	-0,0812	-0,0241	0,0019587
-0,9531	-0,937500	-0,94531	-0,0241	0,0039	-0,0000934
-0,9531	-0,945313	-0,94922	-0,0241	-0,0101	0,0002429
-0,9492	-0,945313	-0,94727	-0,0101	-0,0031	0,0000311
-0,9473	-0,945313	-0,94629	-0,0031	0,0004	-0,0000012
-0,9473	-0,946289	-0,94678	-0,0031	-0,0013	0,0000042

Ответ: х-0,94653.