3.4. Модифицированный метод Ньютона

Рассмотренный выше метод Ньютона требует вычисления производной на каждом шаге. В некоторых случаях это может существенно снизить эффективность метода (в смысле затрат машинного времени). Поэтому в тех случаях, когда вычисление производной сопряжено с существенными затратами машинного времени, используют модифицированный метод Ньютона, в котором производная вычисляется только в точке начального приближения :

 

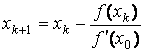. (2.19)

 

5. Метод секущих

Е ще одна модификация метода Ньютона связана с приближенным вычисление производной в окрестности точки по формуле

 

.

 

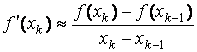Подставляя это выражение в формулу Ньютона (2.15), приходим к формуле

 

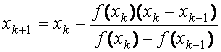, , (2.20)

 

которая определяет метод секущих. Название метода связано с его геометрической интерпретацией (см. рис. 2.10). Секущая, проведенная через точки и , пересекает ось абсцисс в точке , значение которой определяется формулой (2.20).

Для того, чтобы начать итерационный процесс в методе секущих необходимо задать два начальных приближения: нулевое и первое . На практике, как правило, поступают следующим образом: нулевое приближение выбирают аналогично выбору начального приближения в методе Ньютона, а в качестве первого приближения выбирают величину , где e – заданная погрешность. Эти значения используются для нахождения последующего (второго) приближения по формуле (2.20). Затем, значения и используют для определения третьего приближения и т.д. Альтернативно, в качестве нулевого и первого приближений могут быть выбраны границы отрезка локализации корня, если они известны. В этом случае первая итерация метода секущий даст результат, аналогичный методу хорд. Для завершения итерационного процесса можно воспользоваться условием (2.14).

Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной и поэтому оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной затруднено или невозможно, например, если функции получена в ходе численных расчетов, а не задана аналитически.

По алгоритму метод секущих близок к методу хорд, однако в отличие от последнего начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны; кроме того при уточнении корня не проверяются знаки функции .

 

3.5. Метод простых итераций

Теперь рассмотрим более общий итерационный метод уточнения корней. Представим исходное уравнение в виде

. (2.21)

 

О том как преобразовать исходное уравнение к виду (2.21) буден рассказано ниже.

Пусть нам известно начальное приближение к корню ( ). Подставив его в правую часть уравнения (2.21) получим новое приближение , затем аналогичным образом получим и так далее,

, . (2.22)

 

Оказывается, что при определенных свойствах функции последовательность , определяемая по формуле (2.22), сходится к корню уравнения . Необходимо установить при каких условиях итерационный процесс (2.22) будет сходящимся.

В начале рассмотрим графически процесс получения приближений в методе простых итераций (рис. 2.11). При решении уравнения (2.21) необходимо отыскать точку пересечения кривой и прямой . На рисунке 2.11, (а) изображена некоторая кривая , которая может представлять собой любую функцию, но сейчас для нас важно то обстоятельство, что производная этой функции в окрестности корня положительна и меньше 1. Пусть – корень уравнения, который, естественно, предполагается неизвестным. Выберем начальное приближение в точке . Следующее приближении , в соответствии с (2.22), будет равно . Для того, чтобы отобразить на графике можно провести через точку прямую, параллельную оси OX, до пересечения с прямой , а затем в точке пересечения этих прямых опустить перпендикуляр на ось OX, который и отметит положение точки . Аналогично получаются все последующие приближения. Из рисунка видно, что они сходятся к корню. Напомним, что для рассмотрения мы взяли функцию, производная которой положительна и меньше 1.

 

Рассмотрим теперь другую функцию , производная которой отрицательна, но меньше 1 по абсолютному значению. Этот случай изображен на рисунке 2.11, в. Последовательные приближения также сходятся к корню, но на этот раз каждое последующее приближение находится с противоположной стороны от корня. В то время как в первом случае все последовательные приближения находились с одной стороны от корня.

Наконец, рассмотрим случай, когда производная функции больше 1 (рис. 2.11, б) и меньше -1 (рис. 2.11, г). В обоих случаях каждое последующее приближение отстоит дальше от корня, т.е. итерационный процесс расходится. Из сказанного выше можно предположить, что итерационный процесс, определяемый формулой (2.22) сходится при условии, что производная меньше 1 по абсолютной величине.

Математически условие сходимости можно установить следующим образом. Представим k-е и (k+1)-е приближения в форме

 

, ,

 

где и – отклонения приближений от корня.

Функцию вблизи точки приближенно заменим первыми двумя членами ряда Тейлора. Тогда итерационная формула (2.22) примет вид

 

,

 

но поскольку является корнем уравнения, то первые слагаемые в правой и левой частях этого выражения тождественно равны и, следовательно

 

.

 

Для сходимости итерационного процесса необходимо, чтобы погрешность на каждом шаге убывала

,

 

откуда следует, что в окрестности корня должно выполняться условие

 

. (2.23)

 

Таким образом, для того чтобы итерационный процесс (2.22) был сходящимся, необходимо, чтобы абсолютная величина производной в окрестности корня была меньше единицы. Если это условие выполняется на отрезке на котором локализован корень, то в качестве начального приближения можно взять любую точку из этого отрезка . Скорость сходимости зависит от абсолютной величины производной : чем меньше вблизи корня, тем быстрее сходится процесс.

Преобразование уравнения к итерационному виду. Переход от уравнения (2.1) к уравнению в итерационной форме (2.21) можно осуществить различными способами в зависимости от вида функции . При таком переходе необходимо построить функцию так, чтобы выполнялось условие сходимости (2.23).

В качестве примера рассмотрим уравнение , один из корней которого расположен в интервале . Преобразуем это уравнение к виду (2.21) следующим образом: . Проверим условие сходимости для средней точки интервала локализации :

 

, , .

 

Очевидно, что условие сходимости (2.23) не выполнено. Преобразуем уравнение к итерационному виду другим способом: и вновь проверим условие сходимости:

 

, , .

 

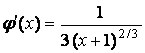Видно, что в этом случае условие сходимости выполнено.

Теперь рассмотрим один из общих алгоритмов перехода от уравнения к уравнению . Умножим левую и правую части уравнения на произвольную константу и добавим к обеим частям неизвестное x. При этом корни исходного уравнения не изменятся

 

или

. (2.24)

 

Уравнение (2.24) эквивалентно уравнению (2.21) с функцией . Произвольный выбор константы t позволяет обеспечить выполнение условия сходимости (2.23). Поскольку в данном случае , значение t следует выбирать, так чтобы в окрестности корня выполнялось условие

 

. (2.25)

 

Желательно выбрать величину t такой, чтобы , тогда сходимость будет двухсторонней (рис. 2.11, в). В этом случае в качестве критерия окончания итерационного процесса можно использовать соотношение (2.14).

Ø Замечание. При сходимости последовательных приближений к корню с разных сторон, что имеет место при в окрестности корня (рис. 2.10, в), величина превосходит истинную погрешность, т.е. , и критерий окончания итерационного процесса (2.14) является вполне объективным. Если же , то сходимость к корню носит односторонний характер (рис. 2.11, а), и условие может выполниться гораздо раньше нужного требования . В этом случае контроль достигнутой точности лучше осуществлять по проверке неравенства

 

,

 

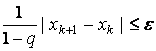где .

Наибольшую скорость сходимости в методе простых итераций получим при . Этого можно добиться, если выбрать параметр t зависящим от x в виде

. (2.26)

 

При этом итерационная формула (2.22) переходит в формулу Ньютона

 

.

 

Таким образом, метод Ньютона можно трактовать как частный случай метода простых итераций, обладающий максимальной скоростью сходимости.