3.3. Метод Ньютона (метод касательных)

Пусть нам известно начальное приближение к корню (вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой (рис. 2.8). Эта касательная пересечет ось абсцисс в точке , которую будем рассматривать в качестве следующего приближения. Значение легко н айти из рисунка:

 

,

 

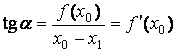выражая отсюда , получим

.

 

Аналогично могут быть найдены и следующие приближения. Формула для k+1-го приближения имеет вид

 

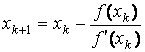, (2.15)

 

Из формулы (2.15) вытекает условие применимости метода: функция должна быть дифференцируемой и в окрестности корня не должна менять знак.

Для окончания итерационного процесса могут быть использованы условия (2.12) или (2.14).

Ø Замечание 1. В методе Ньютона, в отличие от предыдущих методов, не обязательно задавать отрезок , содержащий корень уравнения, а достаточно найти некоторое начальное приближение корня .

Ø Замечание 2. Формула метода Ньютона может быть получена и из других соображений. Зададимся некоторым начальным приближением корня . Заменим функцию f(x) в окрестности точки отрезком ряда Тейлора:

 

,

 

и вместо нелинейного уравнения решим линеаризованное уравнение

 

 

рассматривая его решение как следующее (первое) приближение к искомому значению корня. Решение этого уравнение очевидно:

 

 

Повторяя это процесс приходим к формуле Ньютона (2.15).

 

Сходимость метода Ньютона. Выясним основные условия сходимости последовательности значений , вычисляемых по формуле (2.15), к корню уравнения (2.1). Предполагая, что дважды непрерывно дифференцируема, разложим в ряд Тейлора в окрестности k-го приближения

 

.

 

Разделив последнее соотношение на и перенеся часть слагаемых из левой части в правую, получим:

 

.

 

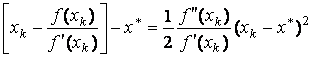Учитывая, что выражение в квадратных скобках согласно (2.15) равно , переписываем это соотношение в виде

 

.

 

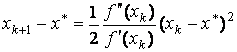Отсюда

 

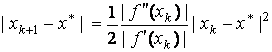. (2.16)

 

Из (2.16) следует оценка

 

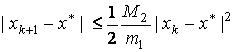, (2.17)

 

где , .

Очевидно, что ошибка убывает, если

 

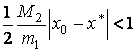. (2.18)

 

Полученное условие означает, что сходимость зависит от выбора начального приближения.

Оценка (2.17) характеризует скорость убывания погрешности для метода Ньютона: на каждом шаге погрешность пропорциональна квадрату погрешности на предыдущем шаге. Следовательно, метод Ньютона обладает квадратичной сходимостью.

Выбор начального приближения в методе Ньютона. Как следует из условия (2.18) сходимость итерационной последовательности, получаемой в методе Ньютона, зависит от выбора начального приближения . Это можно заметить и из геометрической интерпретации метода. Так, если в качестве начального приближения взять точку (рис. 2.9), то на сходимость итерационного процесса рассчитывать не приходится.

Если же в качестве начального приближения выбрать точку , то получим сходящуюся последовательность.

В общем случае, если задан отрезок , содержащий корень, и известно, что функция монотонна на этом отрезке, то в качестве начального приближения можно выбрать ту границу отрезка , где совпадают знаки функции и второй производной . Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.